 |
Главная |
Бесконечно малые функции, их свойства
|
из
5.00
|
Функция  называется бесконечно малой при
называется бесконечно малой при 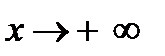 , если её предел равен нулю, т. е.
, если её предел равен нулю, т. е.  . Здесь предел
. Здесь предел 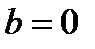 , поэтому
, поэтому 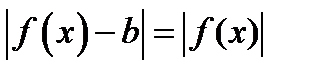 . С учётом определения предела функции можно дать следующее определение бесконечно малой функции: функция
. С учётом определения предела функции можно дать следующее определение бесконечно малой функции: функция  называется бесконечно малой при
называется бесконечно малой при 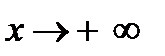 , если для любого
, если для любого 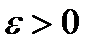 найдётся такое число
найдётся такое число  , что для всех
, что для всех 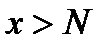 будет выполняться неравенство
будет выполняться неравенство  или символически
или символически

Например, функция  является бесконечно малой при
является бесконечно малой при 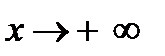 . В самом деле, здесь неравенство
. В самом деле, здесь неравенство  запишется так:
запишется так:  или
или  , т. е.
, т. е. 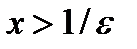 . Итак, для всех
. Итак, для всех  имеем
имеем  для любого
для любого  . Это означает, что
. Это означает, что  есть бесконечно малая функция при
есть бесконечно малая функция при 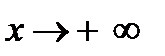 , и в качестве числа
, и в качестве числа  , фигурирующего в определении, можно взять
, фигурирующего в определении, можно взять  .
.
При других способах изменения  определение бесконечно малой функции будет аналогичным (с учётом определения предела). Например, функция
определение бесконечно малой функции будет аналогичным (с учётом определения предела). Например, функция  является бесконечно малой при
является бесконечно малой при  (
( 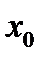 – конечное число), если
– конечное число), если

Свойства бесконечно малой функции
Теорема 4. Если  – бесконечно малые функции при
– бесконечно малые функции при 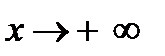 , то их сумма
, то их сумма  также является бесконечно малой функцией, при
также является бесконечно малой функцией, при 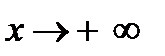 .
.
Доказательство. Пусть  – произвольное число, которое может быть задано сколь угодно малым. Нужно доказать, что для этого числа найдётся такое число
– произвольное число, которое может быть задано сколь угодно малым. Нужно доказать, что для этого числа найдётся такое число  , что для всех
, что для всех 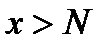 будет выполняться неравенство
будет выполняться неравенство  .
.
Для указанного числа  возьмём число
возьмём число 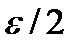 . Так как
. Так как  является бесконечно малой функцией, то для числа
является бесконечно малой функцией, то для числа 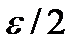 найдётся такое число
найдётся такое число 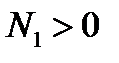 , что для всех
, что для всех  будет выполняться неравенство
будет выполняться неравенство
 . (5)
. (5)
Так как  – бесконечно малая функция при
– бесконечно малая функция при 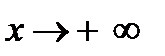 , то найдётся такое число
, то найдётся такое число  , что для всех
, что для всех 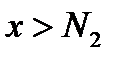 будет выполняться неравенство
будет выполняться неравенство
 . (6)
. (6)
Пусть  – наибольшее из чисел
– наибольшее из чисел  . Тогда для
. Тогда для  имеют место оба неравенства (5), (6). Поэтому с учётом свойства абсолютной величины суммы имеем для всех
имеют место оба неравенства (5), (6). Поэтому с учётом свойства абсолютной величины суммы имеем для всех 

Теорема доказана.
Если  – бесконечно малая функция, то -
– бесконечно малая функция, то - тоже является бесконечно малой функцией. Это ясно из определения, так как
тоже является бесконечно малой функцией. Это ясно из определения, так как 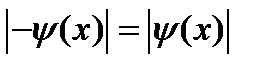 . Ясно также, что разность двух бесконечно малых функций есть снова бесконечно малая функция, т. к. разность можно записать в виде суммы
. Ясно также, что разность двух бесконечно малых функций есть снова бесконечно малая функция, т. к. разность можно записать в виде суммы  .
.
Доказанная теорема сразу распространяется на любое конечное число слагаемых бесконечно малых функций. Можно сказать, что алгебраическая сумма конечного числа бесконечно малых функций – бесконечно малая функция.
Теорема 5.Если  – бесконечно малая функция при
– бесконечно малая функция при 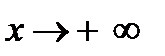 , а
, а  – ограниченная функция на некотором бесконечном интервале
– ограниченная функция на некотором бесконечном интервале  , то произведение
, то произведение  – бесконечно малая функция при
– бесконечно малая функция при 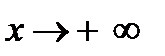 .
.
Доказательство. Пусть  – произвольное число, которое может быть задано сколь угодно малым. Нужно доказать, что для этого числа найдётся такое число
– произвольное число, которое может быть задано сколь угодно малым. Нужно доказать, что для этого числа найдётся такое число  , что для всех
, что для всех 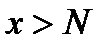 будет выполняться неравенство
будет выполняться неравенство 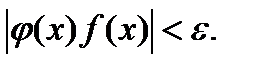 Это будет означать, что рассматриваемое произведение есть бесконечно малая функция при
Это будет означать, что рассматриваемое произведение есть бесконечно малая функция при 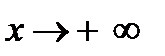 . Так как
. Так как  – ограниченная функция в интервале
– ограниченная функция в интервале  , то существует такое число
, то существует такое число  , что для всех точек интервала
, что для всех точек интервала  , т. е. для всех
, т. е. для всех  , имеет место неравенство
, имеет место неравенство
 . (7)
. (7)
Так как  является бесконечно малой функцией при
является бесконечно малой функцией при 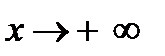 , то для числа
, то для числа  найдётся такое число
найдётся такое число  , что для всех
, что для всех 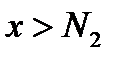 будет выполняться неравенство
будет выполняться неравенство
 . (8)
. (8)
Пусть  – наибольшее из чисел
– наибольшее из чисел  . Тогда для всех
. Тогда для всех  неравенства (7) и (8) выполняются одновременно, поэтому с учётом свойства абсолютной величины произведения для всех
неравенства (7) и (8) выполняются одновременно, поэтому с учётом свойства абсолютной величины произведения для всех  имеем
имеем

Теорема доказана.
|
из
5.00
|
Обсуждение в статье: Бесконечно малые функции, их свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

