 |
Главная |
Приведение к каноническому виду кривых и поверхностей второго порядка
|
из
5.00
|
24. Собственные значения и собственные векторы линейного оператора. Приведение квадратичной формы к каноническому виду.
Пусть 
 линейный оператор, действующий в линейном пространстве.
линейный оператор, действующий в линейном пространстве.
Число  называется собственным значением, а ненулевой вектор
называется собственным значением, а ненулевой вектор 
 соответствующим собственным вектором линейного оператора
соответствующим собственным вектором линейного оператора 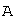 , если они связаны между собой соотношением
, если они связаны между собой соотношением 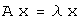 .
.
Пусть 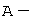 матрица оператора в некотором базисе.
матрица оператора в некотором базисе.
Собственные значения оператора и соответствующие им собственные векторы связаны соотношением 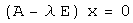 , где
, где  единичная матрица, а
единичная матрица, а  нулевой элемент пространства
нулевой элемент пространства  . Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы
. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы 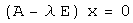 , которое существует тогда и только тогда, когда
, которое существует тогда и только тогда, когда  . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения
. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения  , а собственные векторы -- как решения соответствующих однородных систем.
, а собственные векторы -- как решения соответствующих однородных систем.
Уравнение  называется характеристическим уравнением оператора, а многочлен
называется характеристическим уравнением оператора, а многочлен  характеристическим многочленом оператора.
характеристическим многочленом оператора.
Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:
характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно  ;
;
линейный оператор, действующий в n-мерном линейном пространстве имеет не более  различных собственных значений;
различных собственных значений;
собственные векторы, отвечающие различным собственным значениям, линейно независимы;
если линейный оператор, действующий в n-мерном линейном пространстве  , имеет
, имеет  различных собственных значений, то собственные векторы оператора образуют базис в пространстве
различных собственных значений, то собственные векторы оператора образуют базис в пространстве  ; этот базис называют собственным базисом оператора;
; этот базис называют собственным базисом оператора;
матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.
Приведение квадратичной формы к каноническому виду.
Рассмотрим некоторое линейное преобразование А с матрицей  .
.
Это симметрическое преобразование можно записать в виде:
y1 = a11x1 + a12x2
y2 = a12x1 + a22x2
где у1 и у2 – координаты вектора в базисе 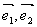 .
.
Очевидно, что квадратичная форма может быть записана в виде
Ф(х1, х2) = х1у1 + х2у2.
Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение  .
.
Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.
Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
.  .
.
При переходе к новому базису от переменных х1 и х2 мы переходим к переменным  и
и  . Тогда
. Тогда

Тогда  .
.
Выражение  называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.
|
из
5.00
|
Обсуждение в статье: Приведение к каноническому виду кривых и поверхностей второго порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

