Элементарные преобразования

· отбрасывание нулевой строки (столбца);

· умножение всех элементов строки (столбца) матрицы на число, не равное нулю;

· изменение порядка строк (столбцов) матрицы;

· прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;

· транспонирование матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, тогда вычисление ранга не представляет труда.

Матрица А называется ступенчатой, если она имеет вид:

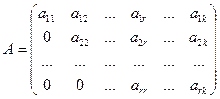, где i=1,2,…,r; r k.

Замечание: условие r k всегда может быть достигнуто транспонированием матрицы.

Очевидно, что ранг ступенчатой матрицы равен r, так как имеется минор r-го порядка, не равный нулю:

Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.

Пример 9 : Найти ранг матрицы

1. Если , то при перестановке строк или столбцов добиваемся того, что . В данном случае поменяем местами, например 1-ю и 2-ю строки матрицы.

2. Если , то умножая элементы 2-й, 3-й, 4-й строк но подходящие числа (именно на , ) и прибавляя полученные числа соответственно к элементам 2-й, 3-й, и 4-й строк, добьёмся того, чтобы все элементы первого столбца (кроме ) равнялись нулю:

3.

~

4. Если в полученной матрице 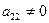(в нашем случае ), то умножая элементы 3-й и 4-й строк на подходящие числа (а именно, на 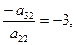), добьёмся того, чтобы все элементы 2-го столбца (кроме , ) равнялись нулю. Если в процессе преобразований получаются строки (или столбцы), целиком состоящие из нулей (как в данном примере), то отбрасываем эти строки (или столбцы):

5.

~

Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например, Поэтому ранг полученной ступенчатой матрицы, а следовательно, и данной матрицы равен 2.

Для рангов матриц справедливы следующие соотношения:

· r(A+B) r(A)+r(B);

· r(A+B) ;

· r(AB) ;

· r(A A)=r(A);

· r(AB)=r(A), если А и В – квадратные матрицы и .

СОБСТВЕННЫЕ ЧИСЛА. СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ.

Пусть дана матрица , и -n-мерный вектор.

Число , удовлетворяющее уравнению (1), называется собственным числом (значением)матрицы А.

Ненулевой вектор 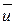, соответствующий числу уравнения (1), называется собственным векторомматрицы А.

Множество собственных чисел матрицы А, называется её спектром. Иногда собственные числа матрицы, называют её характеристическими корнями, а собственные векторы – характеристическими векторами.

Уравнение (1) можно записать в виде (2), где - n- мерный нуль-вектор.

Матрица А имеет собственный вектор , если матрица 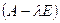вырожденная, то есть её определитель равен нулю: . (3)

Равенство (3) является уравнением n-степени относительно переменной .

.

Уравнение (3) называется характеристическим уравнениемматрицы А, определитель - её характеристическим многочленом.

Итак, чтобы найти собственные числа матрицы, надо составить и решить её характеристическое уравнение.

Чтобы найти собственный вектор, соответствующий собственному числу , надо решить матричное уравнение (2), то есть систему однородных линейных уравнений, матрица которой – вырожденная.

Пример 10: Найти собственные числа и собственные векторы матрицы .

Решение.

Составим и решим характеристическое уравнение .

Итак, матрица А имеет два действительных собственных числа (-2) и 13.

Собственные векторы матрицы А, соответствующие собственному числу , находим решая систему

эта система равносильна одному уравнению

Пусть , тогда Получим, что собственные векторы матрицы А, соответствующие собственному числу имеет вид , где к – любое число, не равное нулю.

Найдем собственные векторы матрицы А, соответствующие собственному числу

Эта система равносильна одному уравнению .

Собственные векторы матрицы А, соответствующие собственному числу имеют вид , где к – любое, не равное нулю, число.

В экономических приложениях полезно использовать некоторые свойства собственных чисел и собственных векторов матрицы.