 |
Главная |
САМОДВОЙСТВЕННЫЕ ФУНКЦИИ
|
из
5.00
|
СПЕЦИАЛЬНЫЕ КЛАССЫ БУЛЕВСКИХ
ФУНКЦИЙ
ОПРЕДЕЛЕНИЕ
Множество функций B  называется замкнутым классом, если [B] = B.
называется замкнутым классом, если [B] = B.
Например, множество {x,  } является замкнутым классом. Рассмотрим пять специальных классов булевских функций, свойства которых будут использованы при нахождении простых необходимых и достаточных условий полноты произвольных систем функций в P2.
} является замкнутым классом. Рассмотрим пять специальных классов булевских функций, свойства которых будут использованы при нахождении простых необходимых и достаточных условий полноты произвольных систем функций в P2.
ФУНКЦИИ, СОХРАНЯЮЩИЕ НОЛЬ
Обозначим как Т0 множество всех таких булевских функций, которые на нулевом наборе значений переменных принимают значение 0.
О таких функциях говорят, что они сохраняют 0, т.е. множество б.ф., сохраняющих ноль, это:
Т0 = {f(x1,...,x n) ½ f(0,...,0) = 0}.
Сформулируем простейшие свойства класса T0.
1. Класс T0 является замкнутым классом функций.
Для проверки справедливости последнего утверждения достаточно проверить, что всякая формула U(f1, . . . , fp), составленная с помощью функций f1, . . . , fp, сохраняющих ноль, представляет функцию fU, которая также сохраняет ноль.
Проведем обоснование этого свойства в соответствии с определением понятия формулы над классом функций.
1.1.Если U = f(x1,. . . , xn), где f(x1, . . . , xn)ÎT0, то
f (0, . . . , 0) = 0и fU = f.
1.2.Если U = f (U1,...,Un), где f (x1, . . . , x n) Î T0, а
U1, . . . ,Un - это или символы переменных или подформулы формулы U, составленные с помощью функций из T0 и символов переменных. Заметим, что поскольку обозначение переменной представляет тождественную функцию I(x) = x, то U1, . . . ,Un можно рассматривать как подформулы, представляющие некоторые функции  из класса T0. Тогда функция f(
из класса T0. Тогда функция f( 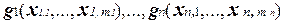 ) также принадлежит классу T0.
) также принадлежит классу T0.
Действительно, f(g1(0,. . . , 0),. . . , gn (0, . . . ,0))= f(0, . . . ,0)=0.
2. Определим число различных функций переменных
x1, . . . , xn, которые содержатся в T0.
Поскольку функции из T0 на всех наборах значений переменных, отличных от нулевого набора, принимают произвольные значения, и таких ненулевых наборов 2n-1, то в T0 содержится ровно  различных булевских функций n переменных.
различных булевских функций n переменных.
ФУНКЦИИ, СОХРАНЯЮЩИЕ ЕДИНИЦУ
Обозначим как T1 множество всех булевских функций, которые на единичном наборе значений переменных принимают значение 1. О таких булевских функциях говорят, что они сохраняют единицу, т.е. Т1 = {f(x1, . . . , xn) ½ f(1, . . . , 1) = 1}.
Класс T1 является замкнутым и содержит  различных функций n переменных. Последние свойства могут быть обоснованы аналогично тому, как это делалось для класса T1.
различных функций n переменных. Последние свойства могут быть обоснованы аналогично тому, как это делалось для класса T1.
САМОДВОЙСТВЕННЫЕ ФУНКЦИИ
Двоичные наборы  и
и  называются противоположными наборами.
называются противоположными наборами.
Противоположные наборы значений переменных в табличном задании булевых функций соответствуют строкам, расположенным симметрично относительно середины таблицы.
Докажем это утверждение. Заметим, что середина таблицы располагается между последним набором верхней половины таблицы (0, 1, . . . , 1) и первым набором значений переменных в нижней половине таблицы (1, 0,. . . , 0).
Тогда, пусть  и
и  - произвольные противоположные наборы. Для определенности будем считать, что s1 =0.
- произвольные противоположные наборы. Для определенности будем считать, что s1 =0.
1. Для набора  , расположенного в верхней половине таблице, определим расстояние до нижнего набора верхней половины таблицы, т.е. количество наборов до набора (0, 1, . . . ,1). Нетрудно видеть, что искомое расстояние представляется числом, имеющим двоичное представление в виде набора
, расположенного в верхней половине таблице, определим расстояние до нижнего набора верхней половины таблицы, т.е. количество наборов до набора (0, 1, . . . ,1). Нетрудно видеть, что искомое расстояние представляется числом, имеющим двоичное представление в виде набора 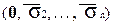 .
.
2. Определим двоичный набор, находящийся на таком же расстоянии от набора (1,0, . . . , 0), являющегося первым набором нижней половины таблицы
Нетрудно проверить, что 10. . . 0+ 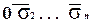 =
=  .
.
Следовательно, набор, отстоящий от (1, 0, . . . , 0) на расстоянии  , - это набор, который является противоположным
, - это набор, который является противоположным  . Поэтому расстояния от противоположных наборов
. Поэтому расстояния от противоположных наборов  и
и  до середины таблицы равны.
до середины таблицы равны.
ОПРЕДЕЛЕНИЕ
Пусть f(x1, . . . , xn) Î P2. Функция g(x1, . . . , xn) Î P2 называется двойственной к функции f, если
g(x1, . . . , xn) =  .
.
Двойственная функция к заданной функции f обозначается как f*.
Нетрудно проверить, что 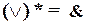 ,
, 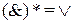 ,
, 
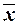 .
.
Кроме того, легко убедиться в справедливости следующего свойства: функция, двойственная к двойственной функции, совпадает с исходной функцией, т.е. справедливо равенство: f** = f.
ОПРЕДЕЛЕНИЕ
Функция f называется самодвойственной, если f = f*.
То есть всякая самодвойственная функция на любых двух противоположных наборах значений переменных принимает противоположные значения. Примерами самодвойственных функций являются тождественная функция f(x) = x и отрицание f(x) = 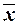 .
.
Множество всех самодвойственных функций обозначается как S.
Установленное ранее свойство симметричности расположения противоположных наборов в табличном задании булевских функций позволяет использовать следующую схему построения табличного задания функции, двойственной к заданной функции.
Пусть f(x1, . . . , xn) - произвольная булевская функция, заданная таблично.
1. Выпишем столбец значений f в обратном порядке.
2. В полученном столбце выполним замену всякого значения в нем на противоположное значение.
Полученный в результате столбец значений функции представляет собой столбец значений двойственной функции f*. Действительно, первое преобразование позволяет по столбцу значений функции f(x1, . . . , xn)получить столбец значений функции f( 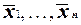 ).
).
Второе преобразование переводит функцию f( 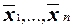 ) в ее отрицание,
) в ее отрицание,  т.е. окончательная функция - это f*.
т.е. окончательная функция - это f*.
Если функция f задана формулой, то для получения формульного представления функции f* можно воспользоваться следующей теоремой.
ТЕОРЕМА 4.7 (О формуле для двойственной функции)
Пусть f(x1, . . . , xn)представляется формулой U (g1,..., gn). Тогда функция f* представляется формулой
U* = U(g*1, . . . , g*n).
Доказательство
Докажем теорему индукцией по глубине формулы U.
1. Базис индукции.Покажем, что если f = 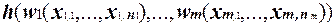 , то
, то  представляется формулой
представляется формулой  . Запишем цепочку равенств:
. Запишем цепочку равенств:

= 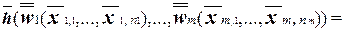
= 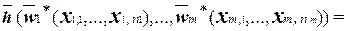
=  .
.
2. Индуктивное предположение. Предположим, что доказываемое в свойство выполняется для всех формул, глубина которых не превосходит n.
3.Индуктивный переход. Пусть f = U(g1,..., gn), где U(g1,..., gn) - это формула глубины n + 1, составленная с помощью символов переменных и функций g1,..., gn
Предположим, что U = h(U1, . . . , Un), где для формул U1, . . . , Un и представляемых ими булевских функций w1, . . . , wn справедлива доказываемая теорема.
Тогда аналогично доказательству базиса индукции можно показать, что 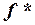 =
= 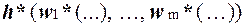 .
.
Поскольку всякая функция  представляется формулой
представляется формулой 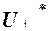 , то
, то 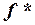 представляется формулой
представляется формулой  , т.е. формулой U(
, т.е. формулой U(  ,...,
,..., 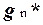 ).
).
|
из
5.00
|
Обсуждение в статье: САМОДВОЙСТВЕННЫЕ ФУНКЦИИ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

