 |
Главная |
Теоретический материал к разделу. 4.1.1 Основные понятия о функциях нескольких переменных
|
из
5.00
|
4.1.1 Основные понятия о функциях нескольких переменных
Определение 1. Функцией двух (трех) переменных называется функция, область определения  которой есть некоторое подмножество на плоскости (в пространстве), а область значений
которой есть некоторое подмножество на плоскости (в пространстве), а область значений 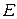 принадлежит действительной оси.
принадлежит действительной оси.
Если  принадлежит плоскости
принадлежит плоскости  , а
, а 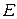 оси
оси  , то такую функцию двух переменных записывают в виде
, то такую функцию двух переменных записывают в виде
 .
.
Пример1. Найти область определения функции  .
.
Решение: Эта функция определена, если  ,
,  , то есть
, то есть  ,
,  . Возведя в квадрат обе части предыдущего неравенства, получим
. Возведя в квадрат обе части предыдущего неравенства, получим  , то есть
, то есть  . Далее, имеем
. Далее, имеем  Данная система будет выполняться, если выполняется одно из следующих соотношений
Данная система будет выполняться, если выполняется одно из следующих соотношений
 либо
либо 
В итоге, область определения функции  можно записать в виде
можно записать в виде
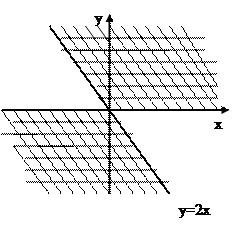
 .
.
Рисунок 1
Геометрически  состоит из двух тупых углов, образованных прямыми
состоит из двух тупых углов, образованных прямыми  , включая границы без точки
, включая границы без точки  (рис.1).
(рис.1).
Пример 2.Найти область определения функции  , где
, где  – положительное число.
– положительное число.
Решение: Функция  принимает действительные значения при условии
принимает действительные значения при условии
 , то есть
, то есть  . Следовательно, областью определения данной функции является круг радиусом
. Следовательно, областью определения данной функции является круг радиусом  с центром в точке
с центром в точке  , включая граничную окружность, то есть
, включая граничную окружность, то есть  .
.
4.1.2 Предел и непрерывность функции нескольких переменных
Определение 2.Число  называется пределом функции
называется пределом функции

в точке  , если для каждого
, если для каждого  найдется такое число
найдется такое число  что при всех
что при всех  из окрестности
из окрестности  , кроме этой точки, выполняется неравенство
, кроме этой точки, выполняется неравенство

и обозначается в виде
 .
.
Практически все свойства пределов, рассмотренные нами ранее для функций одной переменой остаются справедливыми и для пределов функций нескольких переменных, однако практическим нахождением таких пределов мы заниматься не будем.
Определение 3. Функция  называется непрерывной в точке
называется непрерывной в точке  если выполняется три условия:
если выполняется три условия:
1) существует 
2) существует значение функции в точке 
3) эти два числа равны между собой, т.е.  .
.
Пример 3. Найдем все точки, в которых непрерывна функция
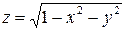 .
.
Как было отмечено выше, эта функция определена в замкнутом круге
 .
.
Внутренние точки этого круга является искомыми точками непрерывности функции, т.е. функция  непрерывна в открытом круге
непрерывна в открытом круге  .
.
4.1.3 Частные производные
Определение 4.Если существует предел  , то его называют частной производной
, то его называют частной производной  по
по  [
[  по
по  ] и обозначают:
] и обозначают:
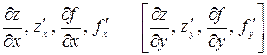 .
.
Из определения 2 следует, что если берется частная производная по какой-либо переменной, то все остальные переменные считаются постоянными.
Пример 4. Дана функция 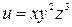 .
.
 .
.
Пример 5. Найти
Найти  ,
,  .
.
Решение: Рассматривая  как постоянную величину, получим
как постоянную величину, получим
 .
.
Рассматривая  как постоянную величину, находим
как постоянную величину, находим
 .
.
4.1.4 Полный дифференциал
Определение 5. Функция  , имеющая представление
, имеющая представление
 , (1)
, (1)
называется дифференцируемой, а её главная (линейная) часть – полным дифференциалом и обозначается 
 (2)
(2)
Из (1) следует, что  . Или
. Или
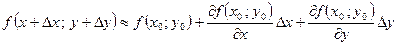
Пример 6. Для 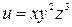 найти
найти  .
.

Пример 7. Вычислить приближённо  .
.
Решение: Рассмотрим функцию  , где
, где  .
.
Тогда 


 .
.
4.1.5 Дифференцирование неявной функции 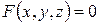
При условии существования и непрерывности  имеем
имеем

Для функции двух переменных  ,
,  .
.
Пример 8.
а) 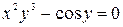 .
.

б) 
 .
.
4.1.6 Производная сложной функции. Полная производная
Пусть задана функция  , где
, где 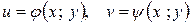 . Тогда, при условии существования непрерывных частных производных функций
. Тогда, при условии существования непрерывных частных производных функций 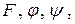 имеем
имеем


Если задана функция  , где
, где 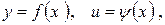 то
то
 - формула полной производной.
- формула полной производной.
Пример 9. Пусть  ,
,  ,
,  .
.
Найдем частные производные сложной функции составленной из этих функций.
 |подставим сюда значения
|подставим сюда значения  и
и  | =
| = 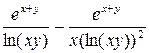 .
.
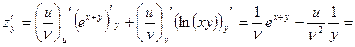
 .
.
4.1.7 Теорема о смешанных производных
Пусть задана функция  , имеющая частные производные
, имеющая частные производные  и
и  . Частные производные от
. Частные производные от  и
и  , если они существуют, будут частными производными второго порядка:
, если они существуют, будут частными производными второго порядка:


Аналогично можно найти частные производные порядка 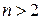 .
.
Теорема 1.Если  и
и  определены и непрерывны в т.
определены и непрерывны в т.  и в некоторой её окрестности,. то в этой точке
и в некоторой её окрестности,. то в этой точке

Теорема 2.При соответствующих условиях теорема 1 верна для смешанных производных порядка 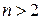 .
.
Пример 10.  .
.
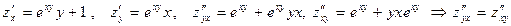 .
.
4.1.8 Касательная плоскость и нормаль к поверхности
Через любую  функции
функции  можно провести касательную плоскость к ее поверхности, проходящей через
можно провести касательную плоскость к ее поверхности, проходящей через  .
.
Ее уравнение будет:
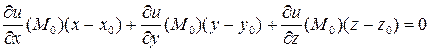 .
.
Прямая, перпендикулярная касательной плоскости к поверхности  в точке касания
в точке касания  называется нормальюк этой поверхности.
называется нормальюк этой поверхности.
В любой точке поверхности  нормаль существует и проходит в направлении градиента функции в этой точке. Ее параметрические уравнения имеют вид
нормаль существует и проходит в направлении градиента функции в этой точке. Ее параметрические уравнения имеют вид
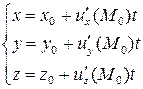 .
.
Если функция задана в виде  , то уравнения касательной плоскости и нормали примут вид:
, то уравнения касательной плоскости и нормали примут вид:
 и
и 
Пример 11. Напишем уравнения касательной плоскости и нормали к поверхности эллиптического параболоида  в точке
в точке 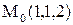 .
.
Решение: Предварительно запишем это уравнение в виде  ,
,
который определяет поверхность уровня 0 функции 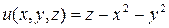 . Отсюда получим
. Отсюда получим  ,
,  ,
, 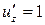 . Следовательно
. Следовательно  ,
,  ,
,  . Подставляя эти значения в уравнения касательной плоскости, получим
. Подставляя эти значения в уравнения касательной плоскости, получим
 , т.е.
, т.е.  .
.
Параметрические уравнения нормали имеют вид
 .
.
4.1.9Определение экстремума функции
Определение 6.Говорят, что функция 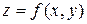 имеет максимум (минимум)
имеет максимум (минимум)  в точке
в точке  , если для всех отличных от
, если для всех отличных от  точек
точек  в достаточно малой окрестности точки
в достаточно малой окрестности точки  выполнено неравенство
выполнено неравенство  (или соответственно
(или соответственно  ).
).
Максимум или минимум функции называется её экстремумом.
Определение 7.Точка (  , в которой дифференцируемая функция
, в которой дифференцируемая функция  может достигать экстремума, называется критической точкой. Она находится путём решения системы уравнений:
может достигать экстремума, называется критической точкой. Она находится путём решения системы уравнений:
 -Это необходимые условия экстремума.
-Это необходимые условия экстремума.
Достаточные условия экстремума.
Пусть
 и
и  .
.
Составим дискриминант 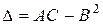 .
.
Тогда: 1) если  , то функция имеет экстремум в точке
, то функция имеет экстремум в точке  , а именно максимум, если
, а именно максимум, если  (или
(или  , и минимум, если А>0 (или С>0); 2) если
, и минимум, если А>0 (или С>0); 2) если  , то экстремума в точке
, то экстремума в точке  нет; 3) если
нет; 3) если  , то вопрос о наличии экстремума функции в точке
, то вопрос о наличии экстремума функции в точке  остается открытым (требуется дальнейшее исследование).
остается открытым (требуется дальнейшее исследование).
Пример 12. Исследовать на экстремум  .
.

Получим две критические точки 

1. Рассмотрим т. 
 имеет минимум.
имеет минимум.

Следовательно, в т. 
 имеет минимум.
имеет минимум.
2. Рассмотрим т.  Тогда
Тогда  - функция в т.
- функция в т.  экстремума не имеет.
экстремума не имеет.
Решение типовых задач
Задача №1.Найти частные производные и частные дифференциалы следующей функции. 
Решение: 

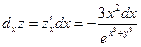 ;
; 
Задача №2. Вычислить значения частных производных  ,
,  ,
,  для данной функции
для данной функции  в точке
в точке  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.
Решение:  ;
;  ;
;  ;
;  ;
;  ;
; 
Ответ:  ;
;  ;
; 
Задача №3.Найти полный дифференциал функции  .
.
Решение: 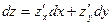
 ;
; 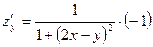 ;
; 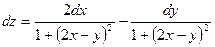
Ответ: 
Задача №4. Вычислить значение производной сложной функции 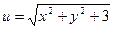 , где
, где  ,
, 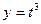 при
при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.
Решение: 
 ;
; 
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 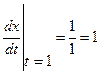 ;
;  ;
; 
Ответ: 
Задача №5.Найти уравнение касательной плоскости и нормали к заданной поверхности S:  в точке
в точке 

Решение: Найдем уравнение касательной плоскости в виде
 . У нас
. У нас  ;
; 
 ;
;  . Тогда уравнение касательной плоскости будет иметь вид:
. Тогда уравнение касательной плоскости будет иметь вид:  или уравнение нормали:
или уравнение нормали:  принимает вид:
принимает вид: 
Задача №6.Найти вторые частные производные функции 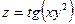 .
.
Убедиться в том, что 
Решение: 


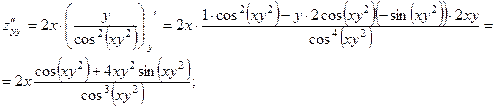
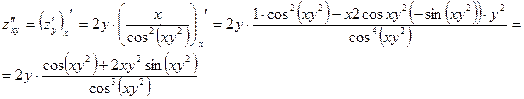

Итак, 
Задача №7.Исследовать на экстремум функцию 
Решение: Используем необходимые условия экстремума функции, чтобы найти стационарные точки
 точка
точка  стационарная точка функции
стационарная точка функции
Вычислим  ,
,  ,
, 
 ;
;  ;
; 
Используя достаточные условия экстремума функции, получаем
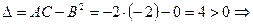 экстремум есть, т.к.
экстремум есть, т.к.  в точке (1,1) находится максимум функции
в точке (1,1) находится максимум функции 
Ответ: 
|
из
5.00
|
Обсуждение в статье: Теоретический материал к разделу. 4.1.1 Основные понятия о функциях нескольких переменных |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

