Многочлен одной переменной

Ключевые слова: квадратный трехчлен, многочлен первой степени, многочлен второй степени. многочлен третьей степени,многочлен n -ной степени.

Общая теория многочленов многих переменных далеко выходит за рамки школьного курса. Мы рассмотрим многочлены одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.

Многочлен ax + b , где a =0 , a, b - числа, x - переменная, называется многочленом первой степени .
Многочлен ax2+bx+c, где a =0 , a , b , c - числа, x - переменная, называется многочленом второй степени (квадратным трёхчленом , квадратичной функцией ).
Многочлен ax3+bx2+cx+d, где a =0 , a , b , c , d - числа, x - переменная, называется многочленом третьей степени.

 

Вообще, многочлен P n ( x ) = a n x n + a n – 1 x n – 1 + a n – 2 x n – 2 + ... + a 1 x + a 0 , где a =0 , ak k=0 1 2 3 n - числа, x - переменная, называется многочленом n -ной степени .
Традиционно an называется старшим коэффициентом , а a0 - свободным членом многочлена.

Действительное число a называется корнем многочлена P n ( x ), если P n ( a ) = 0.

Корень многочлена первой степени легко угадывается: x=−ab. В самом деле: a(−ab)+b=−b+b=0.

Корни квадратного трехчлена можно найти по формулам x1=2a−b+ D x2=2a−b− D ,

выражение D = b2– 4 ac называется дискриминантом квадратного трехчлена , причем только при D > 0 квадратный техчлен имеет корни.

Тогда последнее разложение квадратного трехчлена имеет вид: ax 2 + bx + c = a ( x – x 1 )( x – x 2 ).

Отсюда непосредственно видно, что числа x 1 и x 2 являются корнями квадратного трехчлена ax 2 + bx + c .

Полученная формула ввиду своей важности называется формулой разложения квадратного трехчлена на множители .

Сумма и разность многочленов: .

Суммой и разностью многочленов и называется следующий многочлен:

Степень полученного многочлена не превосходит максимальной степени многочленов и .

Умножение на одночлен: .

Умножим одночлен на многочлен :

т.е. каждый член многочлена умножается на одночлен. Здесь применяем правило работы со степенями.

Умножение многочленов: .

Умножим многочлен на :

В итоге свели операцию умножения многочленов к умножению одночлена на многочлен. Заметим, что при умножении многочленов степени и получается многочлен степени . При умножении многочленов необходимо каждый член одного многочлена умножить на каждый член другого многочлена.

Деление многочленов: .

Разделим многочлен на , т.е. представим выражение в следующем виде:

где -- частное от деления, -- делимое, -- делитель, -- остаток.

При делении многочлена на многочлен , где , нужно найти многочлены и такие, чтобы выполнялось равенство

Существует много способов поиска таких многочленов. В основном используются школьные способы, а именно, деление "уголком" ("столбиком") и метод неопределенных коэффициентов (будут рассмотрены ниже).

1.13

Алгоритм деления с остатком

 

Для любых f(x), g(x) существуют q(x) (частное) и r(x) (остаток), такие, что f(x)=g(x)q(x)+r(x), причем степень r(x) < степени g(x) илиr(x) = 0. Многочлены g(x) и r(x) определены однозначно.

Частное и остаток находят с помощью так называемого правила деления "уголком".

Пример.

 

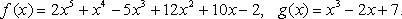
Делители многочлена

 

Делитель многочлена f(x) - многочлен g(x), такой, что

f(x) = g(x)q(x).

Наибольший общий делитель двух многочленов

 

Наибольший общий делитель многочленов f(x) и g(x) - такой их общий делитель d(x), который делится на любой другой их общий делитель.

 

 

1.14

Многочлен делится на многочлен , если существует такой многочлен , что выполняется равенство

(2.1)

Например, из равенства следует, что делится на многочлен и на многочлен .

Многочлен в равенстве (2.1) определяется однозначно. Если бы существовал многочлен , удовлетворяющий равенству (2.1), то мы получили бы, что

(2.2)

откуда

Но многочлен по условию ненулевой, и в силу утверждения или нулевом является многочлен , т.е. многочлен совпадает с .

Многочлен в равенстве (2.1) называется частным от деления на , а - делителем.

Укажем некоторые основные свойства делимости многочленов.

1. Если делится , а делится на , то будет делиться на .

В самом деле, по условию и , а поэтому .

2. Если и делятся на , то их сумма и разность также делятся на .

Из равенств и вытекает .

3. Если делится на , то произведение на любой многочлен также будет делиться на .

Если , то .

Из 2. и 3. вытекает следующее свойство:

4. Если каждый из многочленов делится на , то на будет делиться и многочлен , где - произвольные многочлены.

5. Всякий многочлен делится на любой многочлен нулевой степени.

Если , а с - произвольное число, не равное нулю, то есть произвольный многочлен нулевой степени, то .

6. Если делится на , то делится и на с, где с - произвольное число отличное от нуля.

Из равенства следует равенство .

7. Многочлены , , и только они будут делителями многочлена , имеющими такую же степень, что и .

Действительно, . То есть делится на .

Если делится на , причем степени и совпадают, то степень частного от деления на должна быть равной нулю, то есть , , откуда .

Отсюда вытекает следующее свойство:

8. Тогда и только тогда многочлены , одновременно делятся друг на друга, если , .

Из 1. и 8. вытекает свойство:

9. Всякий делитель одного из двух многочленов , , где , будет делителем и для другого многочлена.

Свойства делимости многочленов могут быть применены для изучения делимости в множестве целых чисел. Выясним, например, для каких целых чисел n числоявляется простым.

Натуральное число, отличное от 1, называется простым, если оно делится только на 1 и на само себя; целое отрицательное число k называется простым, если число -k простое.

Для ответа на поставленный вопрос заметим, что справедливо равенство

(2.3)

и поэтому число делится на и на Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или -1, т.е. выполняется хотя бы одно из равенств

Остается проверить следующие значения n: 3, 1, 0, -3, -1 и -2. При этих значениях n рассматриваемое число равно соответственно 19, -5, 3, 4, так что искомое множество чисел есть

Может возникнуть вопрос: откуда взялось равенство (2.3)? Как мы догадались, что многочлен таким образом раскладывается на множители? Для нахождения разложений такого типа необязательно прибегать к искусственным группировкам, это можно сделать с помощью теории, которая будет изложена ниже.

Из этого примера видно, что уже для решения задач, связанных с делимостью целых чисел, полезно уметь выяснять, делится ли данный многочлен на некоторый другой многочлен (раскладывается ли на множители).Ответ на такой и многие другие вопросы можно найти с помощью деления многочлена с остатком.

 

1.15