 |
Главная |
Производная по направлению
|
из
5.00
|
8.1. Скалярное поле. Поверхности и линии уровня.
Если в каждой точке области 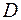 пространства
пространства  определено значение некоторой величины, то говорят, что задано поле данной величины.
определено значение некоторой величины, то говорят, что задано поле данной величины.
Поле называется скалярным, если рассматриваемая величина есть числовая функция.
Примерами скалярных полей являются: поле электрического потенциала, давление в атмосфере, поле температур и другие.
Если в пространстве  введена декартова система координат, то
введена декартова система координат, то
 .
.
Геометрической характеристикой скалярного поля служат поверхности уровня – геометрические места точек, в которых скалярная функция поля принимает одно и то же значение.
Поверхности уровня данного скалярного поля определяются уравнением.
 .
.
Пример. Найти поверхности уровня скалярного поля
 .
.
Решение. Область определения данного скалярного поля находится из неравенства
 , т.е.
, т.е.  .
.
Неравенство показывает, что поле определено вне кругового конуса  и на нем самом, кроме его вершины
и на нем самом, кроме его вершины  .
.
Поверхности уровня определяются уравнением
 , где
, где  , т.е.
, т.е.
 или
или  .
.
Это есть семейство круговых конусов, расположенных вне конуса, с общей осью симметрии  с общей вершиной
с общей вершиной  , в которой данное поле не определено, причем сам конус также входит в это семейство. Скалярное поле называется плоским, если существует декартова система координат, в которой поле задается числовой функцией от
, в которой данное поле не определено, причем сам конус также входит в это семейство. Скалярное поле называется плоским, если существует декартова система координат, в которой поле задается числовой функцией от  переменных.
переменных.
Для 
 .
.
Геометрической характеристикой плоских скалярных полей служат линии уровня – геометрические места точек, в которых скалярная функция имеет одно и то же значение.
Линии уровня определяются уравнением
 , где
, где  .
.
Пример. Написать уравнение линии уровня скалярного поля  , проходящей через точку
, проходящей через точку  , если поле задано неявно уравнением
, если поле задано неявно уравнением
 .
.
Решение. Линии уровня данного скалярного поля определяются уравнением
 , или
, или  .
.
Учитывая тот факт, что  , при
, при  найдем:
найдем:
 .
.
Следовательно, уравнение линии уровня запишется в виде  .
.
8.2. Производная от функции по данному направлению
Пусть скалярное поле  определено в области
определено в области  . Зафиксируем точку
. Зафиксируем точку  и выберем некоторое направление, определяемое вектором
и выберем некоторое направление, определяемое вектором  ; если существует предел
; если существует предел  , то его называют производной функции
, то его называют производной функции  по данному направлению
по данному направлению  в заданной точке
в заданной точке  , где
, где
 ,
,  ,
,  .
.
Пусть в пространстве  введена декартова система координат, тогда
введена декартова система координат, тогда  . Пусть функция
. Пусть функция  дифференцируема в точке
дифференцируема в точке  . Производную функции
. Производную функции  в точке
в точке  по направлению вектора
по направлению вектора  вычисляют по формуле
вычисляют по формуле
 .
.

- направляющие косинусы вектора  .
.
Пример. Вычислим производную скалярного поля
 в точке
в точке  параболы
параболы  по направлению кривой (в направлении возрастания абсцисс).
по направлению кривой (в направлении возрастания абсцисс).
Решение. Пусть касательная к кривой в точке  образует с осью образует с осью  угол угол  : :
 .
Тогда .
Тогда 
| 
|
 .
.
Производная по направлению для плоского скалярного поля будет равна
 .
.
8.3. Градиент скалярного поля
Градиентом скалярного поля  в данной точке
в данной точке  называется вектор
называется вектор
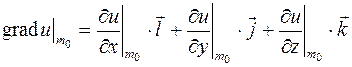 .
.
Градиент и производная по направлению связаны формулой
 ,
,
где  .
.
 по величине и направлению дает наибольшую скорость изменения функции
по величине и направлению дает наибольшую скорость изменения функции  .
.
 в данной точке
в данной точке  направлен по нормали к поверхности уровня, проходящей через точку
направлен по нормали к поверхности уровня, проходящей через точку  .
.
|
из
5.00
|
Обсуждение в статье: Производная по направлению |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

