 |
Главная |
Краткие сведения из алгоритма способа
|
из
5.00
|
Сущность параметрического способа отражается в принципах, положенных в основу составления уравнений поправок. Дальнейшая задача сводится к их решению при условии метода наименьших квадратов.
Для составления уравнений поправок выбирают независимые параметры  . В качестве параметров выбирают величины, которые связаны функциональными зависимостями с результатами измерений. Для всех независимых параметров назначают их предварительные значения
. В качестве параметров выбирают величины, которые связаны функциональными зависимостями с результатами измерений. Для всех независимых параметров назначают их предварительные значения 
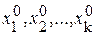 . К ним из уравнивания отыскивают поправки
. К ним из уравнивания отыскивают поправки  .
.
Обозначим численные значения измеренных величин за  , j = 1,.. , n, где n – количество измеренных величин и будем называть их уравниваемыми величинами. Уравненные значения этих величин обозначим за
, j = 1,.. , n, где n – количество измеренных величин и будем называть их уравниваемыми величинами. Уравненные значения этих величин обозначим за  . В качестве независимых параметров обычно принимают координаты пунктов.
. В качестве независимых параметров обычно принимают координаты пунктов.
Независимые параметры связаны функциональными зависимостями с уравниваемыми величинами
 .
.
Это выражение называется уравнением связи, оно справедливо и по отношению к уравненным величинам и уравненным параметрам
 , (19)
, (19)
причем  , где
, где 
 - измеренное значение,
- измеренное значение, 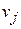 - поправка к измеренной величине,
- поправка к измеренной величине,  - поправки к предварительным значениям параметров.
- поправки к предварительным значениям параметров.
Систему уравнений (19) приводят к линейному виду и получают систему линейных уравнений поправок:
 ,
,
или  , (20)
, (20)
где  - свободный член уравнения поправок;
- свободный член уравнения поправок;
 - коэффициенты уравнений поправок, вычисляемые по формулам:
- коэффициенты уравнений поправок, вычисляемые по формулам:
 . (21)
. (21)
В матричной форме записи система параметрических уравнений имеет вид:
 , (22)
, (22)
где  - вектор-столбец поправок в измеренные величины, количество строк которого (n) совпадает с количеством измеренных величин;
- вектор-столбец поправок в измеренные величины, количество строк которого (n) совпадает с количеством измеренных величин;
 - матрица коэффициентов уравнений поправок, количество строк матрицы соответствует количеству измеренных величин(n), а столбцов – количеству параметров (k);
- матрица коэффициентов уравнений поправок, количество строк матрицы соответствует количеству измеренных величин(n), а столбцов – количеству параметров (k);
 - вектор поправок к приближенным значениям параметров;
- вектор поправок к приближенным значениям параметров;
 - вектор свободных членов уравнений поправок.
- вектор свободных членов уравнений поправок.
Для приведения системы уравнений к равноточному виду и переходу к системе нормальных уравнений умножим систему (22) слева на  , где
, где  - транспонированная матрица коэффициентов уравнений поправок; P– диагональная матрица весовых коэффициентов измеренных величин. Веса измеренных величин определяются по формуле
- транспонированная матрица коэффициентов уравнений поправок; P– диагональная матрица весовых коэффициентов измеренных величин. Веса измеренных величин определяются по формуле  , где
, где  - ошибка единицы веса, назначаемая до уравнивания,
- ошибка единицы веса, назначаемая до уравнивания,  - средняя квадратическая ошибка jизмерения. Система нормальных уравнений имеет вид:
- средняя квадратическая ошибка jизмерения. Система нормальных уравнений имеет вид:
 , (23)
, (23)
где  - матрица коэффициентов нормальных уравнений;
- матрица коэффициентов нормальных уравнений;
 .
.
Решение системы (23) находим в виде
 , (24)
, (24)
где  - матрица, обратная к матрице нормальных уравнений.
- матрица, обратная к матрице нормальных уравнений.
Подставив решение системы нормальных уравнений в выражение (22), найдем вектор поправок в измеренные величины.
После этого необходимо произвести оценку точности. Вычисляют ошибку единицы веса после уравнивания по формуле :
 , (25)
, (25)
где n –число всех измерений,
k – число параметров;
VT – транспонированный вектор поправок в измеренные величины;
Р – матрица весов измеренных величин;
V - вектор поправок в измеренные величины.
Точность определения параметров из уравнивания характеризуется величиной средней квадратической ошибки, значение которой определяется из соотношения  , где Q–обратные веса параметров, являющиеся диагональными элементами матрицы
, где Q–обратные веса параметров, являющиеся диагональными элементами матрицы  .
.
|
из
5.00
|
Обсуждение в статье: Краткие сведения из алгоритма способа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

