На рисунках 4.3-4.4 приведены формы для введения начальных данных и расчетов прямым методом

 

Рисунок 4.3 – Форма введения начальных данных для расчетов прямым методом

 

Рисунок 4.4 – Форма для выведения результатов расчетов прямым методом

 

Для выполнения лабораторной работы необходимо осуществить такую последовательность этапов:

1. Задать конечный спрос и матрицу коэффициентов прямых затрат для итерационных методов.

2. Для прямого метода изменить на n% величину конечного спроса в одной из семи отраслей:

­ сельское, лесное и рыбное хозяйство;

­ тяжелая промышленность;

­ легкая промышленность;

­ строительство;

­ энергетика;

­ транспорт и связь;

­ услуги.

В работе необходимо выполнить вычисления, изменяя конечный спрос в отраслях. Проанализировать изменение валового выпуска всех отраслей при изменении конечного спроса в этих отраслях.

 

4.5 Содержание отчета

 

Отчет по лабораторной работе должен содержать

1) цель работы;

2) исходные данные для итерационных методов, а также для прямого метода;

3) расчеты для итерационных методов;

4) таблицу результатов для прямого метода;

5) один из алгоритмов (какой именно, задает преподаватель);

6) выводы по работе, в которых нужно проанализировать результаты использования итерационного и прямого методов расчета балансовых моделей.

 

4.6 Контрольные вопросы и задания

 

1.Чем отличаются два итерационных метода: метод Якоби и метод Гаусса-Зейделя?

2. Докажите правильность расчетов по методу Гаусса-Зейделя значений Х₁ и Х₂ по формуле (4.2) для 1-й (2-й, 3-й) итерации.

3. Чему будет равняться показатель темпов прироста валового выпуска для прямого метода, если вектор имитационных значений конечного спроса совпадает с вектором базовых значений конечного спроса?

4. Какое экономическое содержание несет в себе нулевое значение коэффициента ?

5. Выполнить лабораторную работу по данным варианта (таблица 4.3), заданного преподавателем.

 

Таблица 4.3 – Исходные данные по вариантам

Номер варианта	Матрица коэффициентов прямых материальных расходов	Конечный спрос	Количество валовой продукции

 

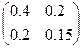
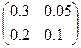
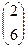
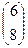
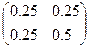
5 МОДЕЛЬ определения равновесных цен

 

5.1 Цель лабораторной работы

 

Целью лабораторной работы является исследование ценового аспекта эффекта распространения и построение ценовой модели межотраслевых связей, а также определение равновесных цен с помощью прикладной программы.

В лабораторной работе необходимо проанализировать изменения ценовых параметров:

1. при росте зарплаты на 10 %;

2. при падении зарплаты на 10 %;

3. при росте прибыли на 10 %.

 

5.2 Методические указания по организации самостоятельной работы студентов

 

При подготовке к лабораторной работе студенту необходимо ознакомиться с теоретическими вопросами относительно модели Леонтьева, балансовой модели на основе модели Леонтьева. Эти вопросы хорошо освещены в [12, с. 54-59, 16, с. 171-176].

Перед выполнением работы студент должен

знать:

1) экономическое содержание коэффициентов прямых материальных затрат;

2) условия производительности матрицы коэффициентов прямых материальных затрат;

3) этапы расчета задачи по модели Леонтьева;

4) содержание квадрантов схемы межотраслевого баланса.

уметь:

1) найти вектор валовой продукции, если известны матрица коэффициентов прямых материальных затрат и вектор конечной продукции;

2) найти межотраслевые потоки продукции;

3) найти по данным первых двух квадрантов схемы межотраслевого баланса условно-чистую продукцию по отраслям и проверить правильность расчетов схемы.

 

5.3 Описание метода лабораторной работы

 

Объектом исследования лабораторной работы является механизм образования равновесной цены на рынке двух товаров.

В лабораторной работе основное внимание уделяется рассмотрению межотраслевого баланса производства и распределения продукции (таблица 5.1) по столбцам.

 

Таблица 5.1 – Межотраслевой баланс производства и распределения продукции

Производящие отрасли	Потребляющие отрасли	Конечный спрос 1	Количество валовой продукции 2
1	2	...
1 2 . . . n	х11 x21 . . . xn1	x12 x22 . . . xn2	... ... I ...	1 2 . . . n	х11 x21 . . . xn1	x12 x22 . . . xn2
Количество условно-чистой продукции	E1	E2	III	Количество условно-чистой продукции	E1	E2
Количество валовой продукции	x1	x2		Количество валовой продукции	x1	x2

 

Столбец i стоимостного межотраслевого баланса может быть показан так

 

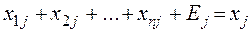, (5.1)

j=1..n,

где – межотраслевые потоки продукции, i=1...n;

Еj – количество условно-чистой продукции;

хj – количество валовой продукции.

Из формулы (5.1), на основе использования выражений

 

, (5.2)

 

получаем

, (5.3)

 

где еj –величина добавленной стоимости, которая приходится на единицу продукции отрасли, она называется долей добавленной стоимости.

Если для базового периода цены всех товаров принять за единицу, то при замене E_j на e_j цены будут определяться по формуле

 

, (5.4)

 

в матричном виде систему уравнения (5.4) можно представить как

 

, (5.5)

где

.

 

Матрица является транспонированной матрицей А,то есть матрицей, в которой сроки и столбцы взаимно переставлены.

Решая (5.5), получаем

 

. (5.6)

 

Уравнения (5.5) и (5.6) получили название модели равновесных цен. Эта модель тождественна модели объемов выпуска, а именно:

а) вектор объема выпуска вектору цен;

б) обратная матрица Леонтьева ценовому матричному мультипликатору ;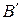

в) вектор конечного спроса вектору частиц добавленной стоимости.

Таким образом, модель объемов выпуска и ценовую модель называют двойственными. Используя (5.4), (5.5), (5.6), можно выяснить, как с помощью структуры ресурсов, которые потребляет каждая отрасль, изменяется структура цен при изменении величины добавленной стоимости. Эффект распространения , вызванный изменением доли добавленной стоимости на определяется как

 

. (5.7)

 

Если величину и долю добавленной стоимости представить как

 

, (5.8)

 

где – зарплата;

– прибыль;

– остаток.

, , , (5.9)

 

то при росте зарплаты на a% изменение величины и доли добавленной стоимости описывается таким образом

 

. (5.10)

 

Аналогичные изменения происходят при росте прибыли.

 

5.4 Порядок выполнения работы и методические указания по ее выполнению

 

Программа лабораторной работы анализирует эффект распространения для ценовых параметров, предусматривая три варианта имитационных значений для долей добавленной стоимости:

1) при росте зарплаты на 10 %;

2) при падении зарплаты на 10 %;

3) при росте прибыли на 10 %.

При запуске программы пользователь попадает на форму, которая не имеет начальных данных, только главное меню программы, клавиши управления и перечень отраслей .

Структура главного меню программы представлена на рисунке 5.1.

 

Рисунок 5.1 – Главное меню программы

 

Начальные данные нужно взять у преподавателя, или загрузить из файла source.dat из клавиши F3.

После этого на экране появится форма, приведенная на рисунке 5.2.

 

Рисунок 5.2 – Форма для введения начальной информации

 

Также в этом окне приведены значения величины добавленной стоимости при каждом есть три варианта событий: рост или падение зарплаты на 10%, рост прибыли на 10% (три нижних строки).

На рисунках 5.3-5.5 приведены формы результата вычисления ценового эффекта распространения, то есть каким образом изменится цена на товары при возникновении вышеупомянутых событий.

 

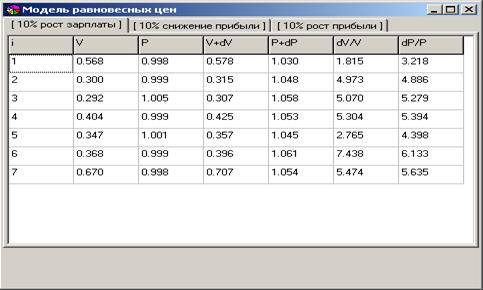
Рисунок 5.3 – Форма результатов расчетов для 10 %-го роста зарплаты

 

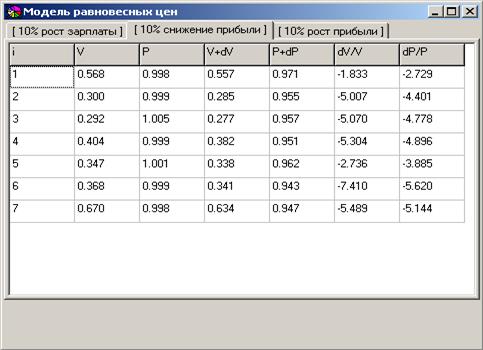
Рисунок 5.4 – Форма результатов расчетов для 10 %-го падения зарплаты

 

Рисунок 5.5 – Форма результатов расчетов для 10 %-го роста прибыли

 

Для выполнения лабораторной работы необходимо ввести начальные данные, после этого по результатам расчетов проанализировать, как изменились цены по отраслям производства.

 

5.5 Содержание отчета

 

Отчет по лабораторной работы должен содержать:

1) цель работы;

2) теоретические основы модели равновесных цен;

3) форму начальных данных;

4) формы с результатами расчетов;

5) выводы, в которых нужно описать, как при изменении факторов, которые влияют на величину и долю добавленной стоимости, изменяются цены на продукцию отраслей.

 

5.6 Контрольные вопросы и задания

 

1. Что такое доля добавленной стоимости?

2. В чем заключается двойственность модели выпуска и ценовой модели?

3. На цены в каких отраслях, судя по результатам лабораторной работы, роста прибыли (зарплаты) повлияли больше всего?

4. Из каких элементов состоит величина добавленной стоимости?

5. Выполнить лабораторную работу по данным варианта (рисунки 5.6-5.13), заданного преподавателем.

 

Рисунок 5.6 – Начальные данные варианта 1

 

Рисунок 5.7 – Начальные данные варианта 2

 

Рисунок 5.8 – Начальные данные варианта 3

 

Рисунок 5.9 – Начальные данные варианта 4

 

Рисунок 5.10 – Начальные данные варианта 5

 

 

Рисунок 5.11 – Начальные данные варианта 6

 

Рисунок 5.12 – Начальные данные варианта 7

 

Рисунок 5.13 – Начальные данные варианта 8

 

6 АГРЕГИРОВАНИЕ ОТРАСЛЕЙ В МЕЖОТРАСЛЕВОМ БАЛАНСЕ

 

6.1 Цель работы

 

Цель лабораторной работы – изучение механизма агрегирования межотраслевого баланса производства и распределения продукции и использования его на практике. Лабораторная работа включает:

1) анализ межотраслевого баланса производства и распределения продукции для 10 отраслей;

2) построение межотраслевого баланса производства и распределения продукции, полученного после объединения трех заданных отраслей;

3) вычисление матрицы коэффициентов прямых материальных затрат аналитическим методом;

4) вычисление матрицы коэффициентов прямых материальных затрат матричным методом;

5) сравнение полученных результатов.

 

6.2 Методические указания по организации самостоятельной работы студентов

 

Во время подготовки к лабораторной работе необходимо ознакомиться с теоретическими основами агрегирования. Этот вопрос хорошо отражен в работах [2, с.63-66, 12, с. 84-86, 16, с. 176-180].

Перед выполнением лабораторной работы студент должен

знать:

1) суть агрегирования;

2) существующие методы агрегирования;

3) составляющие межотраслевого баланса производства и распределения продукции;

4) что характеризует матрица коэффициентов прямых материальных затрат;

5) аналитический метод агрегирования;

6) матричный метод агрегирования.

уметь:

1) построить агрегированный межотраслевой баланс производства и распределения продукции на основе использования аналитического метода агрегирования;

2) вычислить матрицу коэффициентов прямых материальных затрат на основе использования аналитического метода агрегирования;

3) вычислить матрицу коэффициентов прямых материальных затрат на основе использования матричного метода агрегирования.

 

6.3 Описание методов лабораторной работы

 

В экономико-математическом моделировании актуальной является задача агрегирования отраслей. Агрегирование позволяет превратить сложную модель в простую или уменьшить размерность модели. Это позволяет минимизировать материальные, финансовые, трудовые и другие затраты.

Начальными данными в модели агрегирования выступает межотраслевой баланс производства и распределения продукции (таблица 5.1), который содержит шахматную таблицу, векторы конечной, валовой и условно-чистой продукции.

В межотраслевом балансе производства и распределения продукции рассматриваются n отраслей.Необходимо построить новый межотраслевой баланс на основе объединения некоторых, заранее заданных отраслей и определить по новой модели матрицу коэффициентов прямых материальных затрат.Пусть это будут к, l и r отрасли (к, l, r)=1,....n. Номер новой отрасли обозначим m. Сформулированную задачу можно решить аналитическим и матричным методами.

В аналитическом методе для определения межотраслевых потоков новой отрасли используются формулы

 

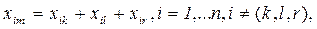(6.1)

 

(6.2)

 

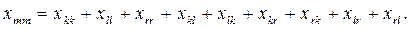(6.3)

 

Количество валовой и конечной продукции новой отрасли равняется

 

(6.4)

 

Коэффициенты прямых материальных затрат отрасли m вычисляются по формулам

(6.5)

 

(6.6)

 

(6.7)

Так как в новых межотраслевом балансе и матрице коэффициентов прямых материальных затрат уменьшились количество строк и столбцов, то номера отраслей необходимо скорректировать.

В матричном методе агрегирование выполняется операции над матрицами. Рассмотрим этот метод для четырех отраслей экономики. Необходимо определить матрицу коэффициентов прямых материальных затрат, если объединятся вторая и третья отрасли.

Новая матрица коэффициентов прямых материальных затрат А* вычисляется по формуле

 

(6.8)

 

где I* – скорректированная единичная матрица;

А – начальная матрица коэффициентов прямых материальных затрат;

В* – скорректированная матрица весовых коэффициентов.

Матрицу I* можно получить в результате сложения соответствующих элементов второй и третьей строк единичной матрицы

 

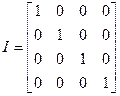, . (6.9)

 

Матрицу В* получают из матрицы весовых коэффициентов В в результате сложения соответствующих элементов второго и третьего столбцов

 

, . (6.10)

 

Весовые коэффициенты определяются таким образом

 

, (6.11)

, (6.12)

, (6.13)

, (6.14)

 

Правильно выполненные расчеты позволяют получить одинаковые результаты на основе использования как аналитического, так и матричного методов.

 

6.4 Порядок выполнения работы и методические указания по ее выполнению

 

Программное обеспечение „AGGressor” написано в среде разработки Borland Delphi 7 и позволяет выполнять агрегирование межотраслевых балансов (МГБ) размерностью 10Х10.

После запуска программы на экране отображается главное окно программы (рисунок 6.1). Активной является вкладка „Исходный МОБ”, где нужно ввести шахматную таблицу баланса (в ячейки, выделенные светло-синим цветом) и вектор конечной продукции (в ячейки, выделенные розовым цветом). Выбор агрегированных отраслей осуществляется с помощью триггеров 1 – 10. Для включения отрасли в список агрегированных необходимо нажать на соответствующий триггер, а для отмены агрегирования отрасли – отжать его. После введения начальных данных необходимо достроить МОБ, для чего нажать кнопку „Достроить баланс”. Если все введено верно, то становится доступной кнопка „Рассчитать” для расчета аггрегированного МОБ, иначе выводится описание ошибки и приводятся координаты ячеек, в которые введены неправильные данные.

 

.

Рисунок 6.1 – Главное окно программы „AGGresor”

 

По окончании расчетов становятся доступными вкладки „Агрегированный МОБ” (рисунок 6.2) и „Матрица прямых затрат” (рисунок 6.3), где выводится конечная информация.

 

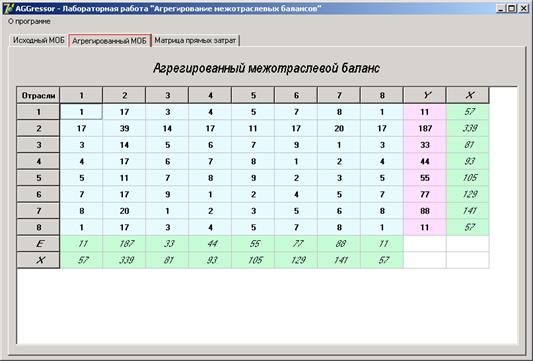
Рисунок 6.2 – Агрегированный МОБ

 

Рисунок 6.3 – Агрегированная матрица прямых материальных затрат

 

6.5 Содержание отчета

 

Отчет по лабораторной работе должен содержать:

1) цель работы;

2) начальный межотраслевой баланс производства и распределения продукции;

3) начальную матрицу коэффициентов прямых материальных затрат;

4) агрегированный межотраслевой баланс производства и распределения продукции;

5) агрегированную матрицу коэффициентов прямых материальных затрат;

6) выводы по работе, в которых нужно оценить правильность выполнения расчетов.

 

6.6 Контрольные вопросы и задания

 

1. Что такое агрегирование?

2. Для чего нужно агрегирование?

3. Как охарактеризовать квадранты межотраслевого баланса производства и распределения продукции?

4. Как определить межотраслевые потоки продукции агрегированной отрасли?

5. Как вычислить количество валовой продукции агрегированной отрасли?

6. Как определить коэффициенты прямых материальных затрат агрегированной отрасли аналитическим методом?

7. Как определить коэффициенты прямых материальных затрат агрегированной отрасли матричным методом?

8. Выполнить лабораторную работу по данным варианта, заданного преподавателем. Таблица 6.1 содержит шахматную таблицу для всех вариантов. Количество конечной продукции задается в соответствии с вариантом из таблицы 6.2. Количество валовой и условно-чистой продукции вычисляется студентами в ходе выполнения лабораторной работы. В таблице 6.3 приведены номера отраслей, которые агрегируются, по вариантам.

Таблица 6.1 – Шахматная таблица (млн. грн.)

Производящие отрасли	Потребляющие отрасли

 

Таблица 6.2 – Количество конечной продукции (млн. грн.)

Номер отрасли	Номер варианта

 

Таблица 6.3 – Номера отраслей, которые агрегируются

Номер варианта	Номер отрасли	Номер варианта	Номер отрасли

РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА

 

1. 1 Витлинский в.В. Моделирование экономики: Навч. пособие. – К.: КНЕУ, 2003.- 408с.

2. 2 Пономаренко о.И. Пономаренко в.О. Системные методы в экономике, менеджменте и бизнесе.: Навч.посибник. К.-Либідь,1995. - 240с.

3. 3 Клебанова т.С., Забродский в.О., Полякова о.Ю., Петренко в.Л. Моделирование экономики: Навч. пособие. – Харьков: Издательство ХДЕУ, 2001.-140 с.

4. 4 Бережна о.В., Бережной в.Г. Математические методы моделирования экономических систем. Навч. пособие. – М.: Финансы и статистика, 2001. – 368с.

5. 5 Хачатрян с.Р. Прикладные методы математического моделирования экономических систем. Науково-метод. Пособие / Московская академия экономики и права. – М.: “Экзамен”, 2002. - 192с.

6. Губин н.М. и др. Экономико-математические методы и модели в планировании и управлении в отрасли связи: Учеб. пособие / Губин н.М., Добронравов а.С., Дорохов б.С. – М.: Радио и связь, 1993. –376с.

7. Малыхин В.И. Математическое моделирование экономики: Учебно-практическое пособие. - М.: Издательство УРАО, 1998. – 160с.

8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Пушкарь, Д.М. Дайитбегов и др.; Под редакторши В.В. Федосеева. – М.: ЮНИТИ, 1999. - 391с.

9. Лопатников л.И. Популярный экономико-математический словарь – М.: Знание, 1990. – 256с.

10. Математическая экономика на персональном компьютере: Пер. с яп. /М. Кубонива, М. Табата, С. Табата, Ю. Хасэбэ; Под редакторши М. Кубонива. – М.: Финансы и статистика, 1991. – 304 с.

Учебное издание

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ

ПО ДИСЦИПЛИНЕ “МОДЕЛИРОВАНИЯ ЭКОНОМИКИ”

для студентов всех форм учебы специальности

"Экономическая кибернетика

 

 

Составители: ПЕТРОВА Роксана Вадимовна

Иванова Виктория Борисовна

 

 

Ответственный выпускающий

Редактор

Компьютерная верстка

 

 

План, поз.

Пидп. до печати Формат 60х84 1/16. Способ печати – ризографія.

Условий. печать. арк. Учет. вид. арк.. Тираж 100.

Зам. № Цена договорная.

 

ХНУРЕ Украина 61166 Харьков, проспект Ленина, 14

__Віддруковано в учебный – научном издательском – полиграфическом центре ХНУРЕ

61166, Харьков, проспект Ленина, 14