Повторные независимые испытания. Формула Бернулли. Примеры

Повторными независимыми испытаниями называют испытания, удовлетворяющие следующим условиям:

1) количество n испытаний конечно;

2) вероятность осуществления случайного события А в каждом из испытаний постоянна:

Примеры повторных испытаний:

1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).

Если вероятность наступления события в каждом испытании постоянна, то вероятность того, что событие наступит ровно раз в независимых испытаниях, равна: , где .

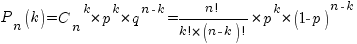
Пример. Вероятность попадания в цель при одном выстреле равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах будет ровно 3 попадания в цель.

Решение. Подставляем в формулу Бернулли данные задачи и получаем:

31. Понятие о центральной предельной теореме. Локальная и интегральная теоремы Муавра—Лапласа, условия их применимости. Примеры.

Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

Закон распределения суммы независимых случайных величин приближается к нормальному закону распределения при неограниченном увеличении , если выполняются следующие условия:

1) все величины имеют конечные математические ожидания и дисперсии:

где .

2) ни одна из величин по значению резко не отличается от остальных:

При решении многих практических задач используют следующую формулировку теоремы Ляпунова для средней арифметической наблюдавшихся значений случайной величины , которая также является случайной величиной (при этом соблюдаются перечисленные два условия):

если случайная величина имеет конечные математическое ожидания и дисперсию , то распределение средней

арифметической 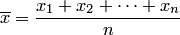, вычисленной по наблюдавшимся значениям случайной величины в независимых испытаниях, при приближается к нормальному закону с математическим ожиданием и дисперсией , то есть

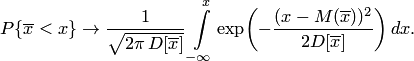
Поэтому вероятность того, что заключена в интервале , можно вычислить по формуле

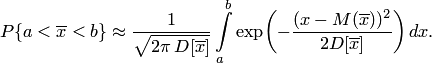
Используя функцию Лапласа, можно записать в удобном для расчётов виде:

Где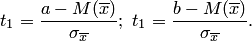

Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный.

32.* Следствия из интегральной теоремы Муавра—Лапласа. Примеры.

Следствие. Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе 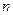независимых испытаний вероятность того, что:

а) число т наступлений события отличается от произведения не более, чем на величину (по абсолютной величине), т.е . ;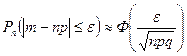

б) частость события заключена в пределах от до (включительно), т.е.

, (31)

Где

в) частость события отличается от его вероятности не более, чем на величину (по абсолютной величине), т.е.

Пример. Вероятность наступления события А в каждом из 900 независимых испытаний равна . Найдите вероятность того, что событие А произойдет: а) 710 раз; б) от 710 до 740 раз.

Решение.

а) Дано: , , , 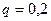. Так как , то воспользовавшись формулами 24-26, четностью функции и таблицей 1 приложения [4, с.553-554], получаем:

б) Дано: , , , , 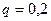. Так как , то воспользовавшись формулами 27-29, нечетностью функции и таблицей 2 приложения [4, с.555], получаем:

Ответ: а) 0,0236; б) 0,7993.

33. Асимптотическая формула Пуассона и условия ее применимости. Примеры.

Применение формулы Бернулли при больших значениях приводит к произведению очень больших 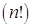и очень малых чисел ( и 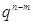), что плохо с вычислительной точки зрения, поэтому приходится пользоваться приближёнными, асимптотическими формулами.

Формула Пуассона

Рассмотрим ситуацию, в которой число испытаний в схеме Бернулли неограниченно увеличивается, а вероятность наступления события в каждом испытании стремится к нулю таким образом, что произведение остаётся величиной постоянной, которую обозначим . В этом случае имеет место соотношение:

Доказательство. По формуле Бернулли

Воспользуемся тем, что по условию или и Формула Бернулли принимает вид:

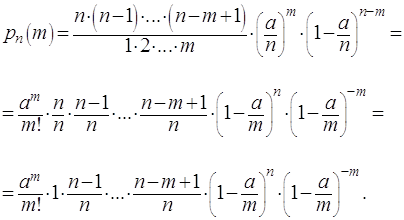
Так как и фиксированы, а стремится к бесконечности, то множители ; … ; и стремятся к единице, а множитель стремится к 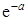, то

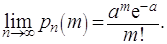
Полученное выражение называется Пуассоновским приближением формулы Бернулли. Эта формула даёт хорошее приближение при достаточно большом и малом (например, и ).

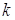Вероятность события, заключающегося в том, что появится не более раз, очевидно, вычисляется по формуле

Пример. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.

Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5).

Находим .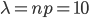

Воспользуемся формулой Пуассона