 |
Главная |
Алгоритм решения векторной задачи
|
из
5.00
|
Рассматривается выпуклая векторная задача математического программирования (ВЗМП) с неоднородными (т. е. имеющие различное направление оптимизации) критериями:
opt F(X) = {max F1(X) = {fk(X), k =  }, (5.5.1)
}, (5.5.1)
min F2(X) = {fk(X), k =  }}, (5.5.2)
}}, (5.5.2)
G(X)£ B, (5.5.3)
X³0, (5.5.4)
где X = {xj, j =  } - вектор переменных; F(X) = {fk(X), k =
} - вектор переменных; F(X) = {fk(X), k =  } - векторный критерий, K - множество (число) индексов критерия;
} - векторный критерий, K - множество (число) индексов критерия;
F1(X) = {fk(x), k =  } - векторный критерий максимизации, каждую компоненту которого желательно максимизировать, K1 - множество (число) индексов критерия, K1 Ì K, (заметим, что (5.5.1), (5.5.3), (5.5.4) представляют собой ВЗМП с однородными критериями максимизации), fk(X), k =
} - векторный критерий максимизации, каждую компоненту которого желательно максимизировать, K1 - множество (число) индексов критерия, K1 Ì K, (заметим, что (5.5.1), (5.5.3), (5.5.4) представляют собой ВЗМП с однородными критериями максимизации), fk(X), k = 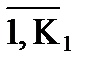 - вогнутые функции;
- вогнутые функции;
F2(X) = {fk(X), k =  } - векторный критерий минимизации, K2 - множество (число) индексов критерия, K2ÌK (заметим, что (5.5.1)-(5.5.4) представляют собой ВЗМП с однородными критериями минимизации), выпуклые функции - fк(X), k =
} - векторный критерий минимизации, K2 - множество (число) индексов критерия, K2ÌK (заметим, что (5.5.1)-(5.5.4) представляют собой ВЗМП с однородными критериями минимизации), выпуклые функции - fк(X), k =  ;
;
G(X)  B - стандартные ограничения, имеющие знаки
B - стандартные ограничения, имеющие знаки  , =, ³..
, =, ³..
Множество допустимых точек S, представленных ограничениями (5.5.3)-(5.5.4) является не пустым.
S = {X Î RN|X ³ 0, G(X) £ B} ¹ Æ
и представляет собой компакт.
Алгоритм решения ВЗМП (5.5.1)-(5.5.4) с равнозначными критериями выполнен в соответствии с принципом оптимальности 1 и представлен в виде ряда шагов.
Алгоритм.
Шаг 1. Решается задача (5.5.1)-(5.5.4) по каждому критерию отдельно, т.е. для "k Î K1 ищется максимум, а для "k Î K2 ищется минимум. В результате решения получим:
X  , f
, f  = fk(X
= fk(X  ), k =
), k =  .
.
Шаг 2. Определяем наихудшую неизменяемую часть критерия f  , k =
, k =  . Для чего решается задача (5.5.1)-(5.5.4) для каждого критерия k =
. Для чего решается задача (5.5.1)-(5.5.4) для каждого критерия k =  на минимум: f
на минимум: f  = min fk(X), G(X) £ B, X ³ 0, k =
= min fk(X), G(X) £ B, X ³ 0, k =  .
.
Решается задача (5.5.1)-(5.5.4) для каждого критерия на максимум: f  = max fk(X), G(X) £ B, X ³ 0, k =
= max fk(X), G(X) £ B, X ³ 0, k =  .
.
Шаг 3. От каждого критерия отнимается его наихудшая неизменяемая часть. fk(X) - f  , k =
, k =  , X Î S.
, X Î S.
В результате получили критерии, которые при переходе от наихудшей точки к оптимальной лежат в пределах:
0 £ (fk(X) - f  ) £ (f
) £ (f  - f
- f  ), k =
), k =  ,
,
0 ³ (fk(X) - f  ) ³ (f
) ³ (f  - f
- f  ), k =
), k =  .
.
Шаг 4. Выполняется стандартная нормализация критериев:
lk(X) = (fk(X) - f  )/(f
)/(f  - f
- f  ), k =
), k =  , X Î S, .
, X Î S, .
где lk(X) - относительная оценка k–го критерия fk(X), k =  .
.
Замечание: "k Î К1, (fk(X) - f  )>0, (f
)>0, (f  - f
- f  )>0, поэтому lk(X)>0; "kÎК2, (fk(X) - f
)>0, поэтому lk(X)>0; "kÎК2, (fk(X) - f  )<0, но меньше нуля и (f
)<0, но меньше нуля и (f  - f
- f  )<0, поэтому lk(X) > 0, "k Î К2.
)<0, поэтому lk(X) > 0, "k Î К2.
В целом по задаче "k Î К относительная оценка lk(X), k =  лежит в пределах 0 £ lk(X) £ 1, "k Î К.
лежит в пределах 0 £ lk(X) £ 1, "k Î К.
Шаг 5. Построение l-задачи.
Построение l-задачи осуществляется в два этапа: первоначально строится максиминная задача оптимизации с нормализованными критериями, которая на втором этапе преобразуется в стандартную задачу математического программирования, названную l-задачей.
а) Любую точку допустимого множества XÎS можно определить набором (множеством) допустимых оценок lk(X), k=  . Определим минимальный уровень l среди множества всех относительных оценок lk(X):
. Определим минимальный уровень l среди множества всех относительных оценок lk(X):
l =  lk(X), "XÎS. (5.5.5)
lk(X), "XÎS. (5.5.5)
Полученный минимальный уровень l максимизируем по XÎS, в результате получим максиминную задачу оптимизации с нормализованными критериями:
lo = 
 lk(X), G(X) £ B, X ³ 0, (5.5.6)
lk(X), G(X) £ B, X ³ 0, (5.5.6)
которая в результате решения дает максимальный уровень lo (среди всех минимальных уровней). Эту же задачу можно представить в стандартном (однокритериальном) виде. Для этого ипользуется второй этап.
б) На втором этапе, используя взаимосвязь выражений l=  lk(X) и l£lk(X), k=
lk(X) и l£lk(X), k=  , преобразуем максиминную задачу (5.5.6) в стандартную задачу математического программирования:
, преобразуем максиминную задачу (5.5.6) в стандартную задачу математического программирования:
lo = max l, (5.5.7)
l - (fk(X) - f  )/(f
)/(f 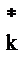 - f
- f  ) £ 0, k =
) £ 0, k =  , (5.5.8)
, (5.5.8)
G(X) £ B, X ³ 0. (5.5.9)
Полученную задачу назовем l-задача.
Шаг 6. Решение l-задачи.
Шаг 7. Конец.
В результате решения l-задачи получаем точку оптимума Xo и максимальную относительную оценку lo, такую, что lo £ lk(Xo), k=  , XoÎS, т. е. является максимальным нижним уровнем для всех относительных оценок lk(Xo), гарантированным результатом в относительных единицах, а в соответствии с теоремой 3, точка {Xo, lo} оптимальна по Парето.
, XoÎS, т. е. является максимальным нижним уровнем для всех относительных оценок lk(Xo), гарантированным результатом в относительных единицах, а в соответствии с теоремой 3, точка {Xo, lo} оптимальна по Парето.
Определим величину каждого критерия в точке Xo из соотношения:
lk(Xo) = (fk(Xo) - f  )/(f
)/(f  - f
- f  ), k=
), k=  , отсюда
, отсюда
fk(Xo) = f  + lk(Xo)(f
+ lk(Xo)(f  - f
- f  ), k=
), k=  , (5.5.10)
, (5.5.10)
т.е. величина любого критерия в оптимальной точке складывается из наихудшей неизменяемой части f  , k=
, k=  , увеличенной на изменяемую часть критерия на допустимом множестве точек S. Причем для всех критериев увеличение осуществляется на величину не хуже максимального нижнего уровня в относительных единицах от изменяемой части критерия.
, увеличенной на изменяемую часть критерия на допустимом множестве точек S. Причем для всех критериев увеличение осуществляется на величину не хуже максимального нижнего уровня в относительных единицах от изменяемой части критерия.
Заметим, что для критериев k =  идет увеличение от f
идет увеличение от f  , k =
, k =  на lk(Xo)(f
на lk(Xo)(f  - f
- f  ), т.к. (f
), т.к. (f  - f
- f  ) > 0, а для k =
) > 0, а для k =  - идет уменьшение от f
- идет уменьшение от f  k =
k =  , на lk(Xo)(f
, на lk(Xo)(f  - f
- f  ), т.к. (f
), т.к. (f  - f
- f  ) < 0, k =
) < 0, k =  .
.
Алгоритм решения ВЗМП (5.5.1)-(5.5.4) с неоднородными критериями покажем на тестовом примере решения векторной задачи линейного (годового плана производственной фирмы).
|
из
5.00
|
Обсуждение в статье: Алгоритм решения векторной задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

