ТЕМА № 4. КОМБИНАТОРИКА

 

Понятие о комбинаторной задаче. Правила суммы и произведения. Перестановки, размещения с повторениями и без повторений, сочетания. Формулы для подсчета числа этих комбинаций.

Литература: [1] с. 38-49; [2] с. 83-87; [3] с. 32-38; [4] с. 23-27; [5] с. 25-33; [6] с. 72-75; [7] с. 17-21.

 

 

КОМБИНАТОРИКА (задания I уровня)

 

1А. Укажите верные формулы:

а) Р_m=m·(m–1)·…·2·1; б) Р_m=m!; в)А = ; г) С = .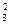

 

1Б. Размещения без повторений из n элементов по m это:

а) m-элементные подмножества n-элементного множества;

б) кортежи длины m из элементов n-элементного множества;

в) упорядоченные m-элементные подмножества n-элементного

множества.

 

2А. Укажите верные формулы:

а) С = ; б) С = 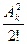; в) С = .

 

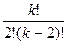2Б. Перестановки из n элементов – это:

а) различные упорядоченные n-элементные множества;

б) кортежи длины n;

в) m-элементные подмножества n-элементного множества.

 

3А. Укажите верные формулы: а) А =n^k; б); А =kⁿ в)А = .

3Б. Сочетания из n элементов по m это:

а) m-элементные подмножества n-элементного множества;

б) кортежи длины m из элементов n-элементного множества;

в) упорядоченные m-элементные подмножества n-элементного

множества.

 

4А. Даны множества А и В, причем n(А)=n₁, n(В)=n₂, АÇВ≠Æ, n(АÇВ)=n₃. Укажите верные равенства: а) n(АÈВ)=n₁+n₂+n₃; б) n(АÈВ)=n₁+n₂; в) n(АÈВ)=n₁+n₂–n₃; г) n(АÈВ)=n₁–n₂.

 

4Б. Разрешения с повторениями из n элементов по m – это:

а) кортежи длины m из элементов n-элементного множества;

б) упорядоченные m-элементные подмножества n-элементного

множества;

в) упорядоченные n-элементные подмножества m-элементного

множества.

 

5А. Даны множества Х и У, причем n(Х)=х₁, n(У)=х₂, ХÇУ≠Æ, n(ХÇУ)=х₃. Укажите верные равенства: а) n(Х×У)=х₁·х₂–х₃; б) n(Х×У)=х₁+х₂; в) n(Х×У)=х₁·х₂; г) n(Х×У)= .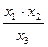

 

5Б. Число различных перестановок элементов множества А={a,b,c,d} вычисляется по формуле:

а) С = 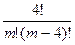; б) Р =1·2·3·4; в) Р =m!

 

0А. Дано множество А={a, b, c, d}. Сколько существует способов упорядочить это множество: а) 4!; б) 3; в) 2⁴; г) .

+ а) 4! Решение: выбран ответ а, поскольку число

б) 3 способов упорядочения 4 - х элементного

в) 2⁴ множества – это число перестановок его

г) элементов Р₄= 4!

 

0Б. Число различных 3-элементных подмножеств множества Х={х₁, х₂, х₃, х₄, х₅} равно: а)2⁵; б) 2³; в) 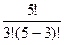; г) 10.

Решение: дано 5-элементное множество, построим всевозможные его 3-элементные подмножества. Неодинаковыми считаются только те, которые имеют неодинаковый состав элементов. Значит, всевозможные трехэлементные подмножества данного множества – это сочетания.

Ответы: в, г.

 

КОМБИНАТОРИКА (задания II уровня)

 

1А. В турнире участвует 6 человек. Сколькими способами могут между ними распределиться места?

 

1Б. Набирая номер телефона, абонент забыл последние две цифры и набрал их наугад, помня, что цифры разные. Сколькими способами он мог это сделать?

 

2А. Сколькими способами можно рассадить 12 гостей на 12 различных стульев?

 

2Б. Сколькими способами можно составить список из 5 учеников?

 

3А. Сколькими способами можно рассадить четырех учащихся на 25 местах?

 

3Б. В меню 4 вида соков и 3 вида нектаров. Сколько существует способов выбора одного напитка?

 

4А. В отделении 12 солдат. Сколькими способами можно составить наряд из трех человек?

 

4Б. Имеется 5 сортов конвертов без марок и 4 сорта марок. Сколькими способами можно выбрать конверт и марку для посылки письма?

 

5А. Из состава участников конференции, на которой присутствует 18 человек, надо избрать делегацию, состоящую из 4 человек. Сколькими способами это можно сделать?

 

5Б. В математической олимпиаде участвуют 14 команд. Сколько существует способов распределения призовых мест?

 

0А. Сколькими способами из 25 студентов можно выбрать делегацию из 5 человек?

 

Решение: Необходимо найти количество 5-элементных подмножеств 25-элементного множества А. Это число сочетаний .

53130

Ответ: делегацию можно выбрать 53130 способами.

 

0Б. В кафе предлагается на десерт 4 вида мороженого, 3 вида пирожных и 2 вида фруктов. Сколько существует способов выбора десерта из одного наименования?

 

Решение: Существует 9 способов выбора десерта из одного наименования, т.к. по правилу суммы 4+3+2=9. Ответ: 9.

 

 

КОМБИНАТОРИКА (задания III уровня)

 

1А. Студенту нужно сдать 4 экзамена за 9 дней. Сколькими способами он может это сделать, если известно, что последний экзамен он сдает на девятый день?

 

1Б. От двух спортивных обществ, в каждом из которых по 40 шахматистов, нужно выделить по 3 человека для участия в соревнованиях. Сколькими способами это можно сделать?

 

2А. Четверо студентов сдают экзамен. Сколькими способами им могут быть поставлены отметки, если известно, что ни один из студентов не получил неудовлетворительной оценки?

 

2Б. Сколько имеется различных шестизначных чисел, у которых первые 3 цифры четные, а следующие 3 – нечетные?

 

3А. Сколько чисел, меньших, чем миллион, можно записать с помощью цифр 9, 8, 7?

 

3Б. Сколькими способами можно разделить 15 яблок и 20 апельсинов между тремя мальчиками?

 

4А. Сколько четырехзначных чисел можно записать, не пользуясь цифрой 8?

 

4Б. На плоскости расположена 21 точка, причем никакие четыре из них не лежат на одной окружности. Сколько окружностей можно провести таким образом, чтобы каждая из них содержала по три из этих точек.

 

5А. Сколько шестизначных чисел, не кратных 5, можно образовать из цифр 1, 2, 3, 4, 5, 6 при условии, что каждая цифра входит в шестизначное число только один раз?

 

5Б. Сколькими способами можно расставить 12 белых и 12 черных шашек на 32 черных полях?

 

0А. Сколько разных комбинаций ответов можно дать на 8 вопросов, если на каждый вопрос отвечают «да» или «нет».

Решение: Необходимо составить кортежи длины 8 из 2-х элементов. Это размещение с повторением : =2⁸=256 (комбинаций). Ответ: можно составить 256 комбинаций ответов.

 

0Б. Сколькими способами можно образовать из группы в 12 мужчин и 8 женщин комиссию, которая бы состояла из 3 мужчин и 4 женщин?

Решение: Из группы 12 мужчин трех мужчин можно выбрать способами, т.е. нужно найти число трехэлементных подмножеств 12 –элементного множества.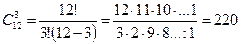

С женщинами аналогично,

Причем на каждый способ выбора мужчин существует способов выбора женщин. Тогда по правилу произведения общее число вариантов выбора комиссии будет равно: =220 × 70=15400

Ответ: 15400.

 

 

КОМБИНАТОРИКА (задания IV уровня)

 

1А. Из 7 гвоздик и 5 тюльпанов надо составить букет из пяти цветов. Сколькими способами это можно сделать, если в него должны входить не более трех тюльпанов?

 

1Б. Докажите, что: =(n–4)².

 

2А. Сколько нечетных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если каждую цифру можно использовать несколько раз?

 

2Б. Докажите, что: А =n· А .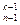

 

3А. Сколько четных чисел, меньших 500, можно составить из цифр 2, 3, 4, 5, 6 так, чтобы ни в одном числе не было повторяющихся цифр?

 

3Б. Докажите, что: А 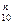·Р_10-n=10·Р₉.

 

4А. Сколько чисел, больших 100, можно записать с помощью цифр 1, 2, 3, 4, если в одном числе каждая цифра используется не более одного раза?

4Б. Докажите, что: С =С +С .

 

5А. Сколько существует различных шестизначных чисел, у которых 3 цифры четные и 3-нечетные.

 

5Б. Докажите, что: =1.

 

 

КОМБИНАТОРИКА (задания V уровня)

 

1. На собрании должны выступить четыре человека: А, В, С, Д. Сколькими способами их можно разместить в списке ораторов, если известно, что В не может выступить, пока не выступит А?

 

2. Для автомобильных номеров используют 10 цифр и 28 букв (кроме ё, й, ь, ъ, ы). Каждый номер состоит из 3 букв и 4 цифр (кроме сочетания цифр 00-00). Какое максимальное число машин получат номера при такой системе?

 

3. Из отряда в 40 человек, среди которых есть рядовой Иванов, назначается в караул 3 человека. Сколькими различными способами может быть составлен караул? В скольких случаях в число караульных попадет рядовой Иванов?

 

4. Восемь женщин и столько же мужчин садятся за круглый стол. Сколько существует способов их рассадки, если два человека одного пола не будут сидеть рядом?

 

5. Из числа трех инженеров и девяти экономистов составлена комиссия из 7 человек. Сколькими способами это можно сделать, если в комиссию должен входить хотя бы один инженер?