 |
Главная |
Уравнение прямой в пространстве, проходящей через две точки
|
из
5.00
|
Рассмотрим прямую в пространстве, проходящую через заданную точку  , с направляющим вектором
, с направляющим вектором  :
:
 .
.
Пусть  - произвольная точка этой прямой. Тогда выполняются равенства:
- произвольная точка этой прямой. Тогда выполняются равенства:
 ,
,
Решая совместно эти уравнения, получим:
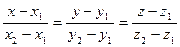
-уравнение прямой, проходящей через две точки  и
и  в пространстве.
в пространстве.
Замечание. Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
Общее уравнения прямой в пространстве
Уравнение прямой можно рассматривать как уравнение линии пересечения двух плоскостей. Плоскость в векторной форме задаётся уравнением
 ×
× 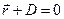 ,
,
где  - нормальный вектор плоскости;
- нормальный вектор плоскости;  - радиус- вектор произвольной точки плоскости.
- радиус- вектор произвольной точки плоскости.
Пусть в пространстве заданы две плоскости: 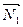 ×
× 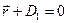 и
и 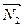 ×
×  , нормальные векторы которых имеют координаты:
, нормальные векторы которых имеют координаты:  ,
,  , а
, а  - радиус- вектор произвольной точки плоскости. Тогда общее уравнение прямой в векторной форме имеет вид:
- радиус- вектор произвольной точки плоскости. Тогда общее уравнение прямой в векторной форме имеет вид:

Общее уравнение прямой в координатной форме имеет вид:

Приведём уравнение прямой в общем виде к каноническому виду.
Для этого найдём координаты произвольной точки прямой и числа  . При этом направляющий вектор прямой находится как векторное произведение векторов нормали к заданным плоскостям
. При этом направляющий вектор прямой находится как векторное произведение векторов нормали к заданным плоскостям

Пример. Найти каноническое уравнение прямой, если прямая задана в виде:

Для нахождения точки  лежащей на прямой, положим
лежащей на прямой, положим 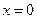 . Тогда
. Тогда
 , т.е.
, т.е.  .
.
Находим компоненты направляющего вектора прямой

Каноническое уравнение прямой примет вид

Основные задачи аналитической геометрии на плоскости и в пространстве
Условия параллельности и перпендикулярности двух прямых (плоскостей)
Пусть в пространстве заданы две плоскости, векторы нормали которых имеют координаты  ,
,  , и две прямые, направляющие векторы которых имеют координаты:
, и две прямые, направляющие векторы которых имеют координаты:  ,
,  .
.
Условие параллельности двух прямых (плоскостей) есть коллинеарность их направляющих (нормальных) векторов:
 ,
,  .
.
Условие перпендикулярности двух прямых (плоскостей) есть ортогональность их направляющих (нормальных) векторов:


Наконец, условием параллельности (перпендикулярности) прямой и плоскости есть перпендикулярность (параллельность) направляющего вектора прямой и нормального вектора плоскости:

 .
.
Угол межу двумя прямыми (плоскостями)
Угол между двумя прямыми (плоскостями) определяется как угол между их направляющими (нормальными) векторами:
 ,
,
 .
.
Угол между прямой и плоскостью
Угол между прямой и плоскостью определяется как угол между прямой и ее ортогональной проекцией на плоскость:
 .
.
Расстояние от точки до прямой и от точки до плоскости.
|
из
5.00
|
Обсуждение в статье: Уравнение прямой в пространстве, проходящей через две точки |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

