 |
Главная |
Бесконечно малые и бесконечно большие функции
|
из
5.00
|
Определение 1. Функция f(x) называется бесконечно большойфункцией при х →x0, если  f(x) =
f(x) =  .
.
Определение 2. Функцияf(x) называется бесконечно малой функцией при х →x0, если  f(x) = 0.
f(x) = 0.
Основные теоремы о пределах функций.
Теорема 1.Предел постоянной величины равен самой постоянной:
 c = c.
c = c.
Теорема 2.Пределсуммы (разности) двух функций равен сумме (разности) их пределов:

 =
=  f(x)
f(x) 
 φ(x).
φ(x).
Теорема 3.Пределпроизведения двух функций равен произведению их пределов:

 =
=  f(x)
f(x) 
 φ(x).
φ(x).
Теорема 4.Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:

 ,
, 
 ¹ 0.
¹ 0.
Теорема 5.(О пределе промежуточной функции) Если в окрестности точки x0выполняются неравенства:
 и
и 
 =
= 
 = А, то
= А, то 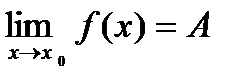 .
.
ТЕХНИКА ВЫЧЕСЛЕНИЯ ПРЕДЕЛОВ
Замечательные приделы.
Пример 1.

Будем говорить, что предел отношения двух функций  есть неопределенность вида
есть неопределенность вида  или
или  , если числитель и знаменатель дроби одновременностремятся к нулю или к бесконечности. Раскрыть эти неопределенности – значит вычислить предел отношения
, если числитель и знаменатель дроби одновременностремятся к нулю или к бесконечности. Раскрыть эти неопределенности – значит вычислить предел отношения  , если он существует или установить, что этот предел не существует.
, если он существует или установить, что этот предел не существует.
Пример 2.


Из рассмотренного примера следует правило: чтобы раскрыть неопределенность вида  при x→x0 функции, заданной в виде отношения двух многочленов, необходимо в числителе и знаменателе выделить множитель x−x0 и дробь на него сократить.
при x→x0 функции, заданной в виде отношения двух многочленов, необходимо в числителе и знаменателе выделить множитель x−x0 и дробь на него сократить.
При вычислении пределов отношения двух многочленов при x→  дляраскрытия неопределенности вида
дляраскрытия неопределенности вида  надо числитель и знаменатель дроби разделить на x в старшей степени.
надо числитель и знаменатель дроби разделить на x в старшей степени.
Пример 3.

Пример 4.


Первый замечательный придел.
Теорема.Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице.

Следствие 1.

Следствие 2.

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5.
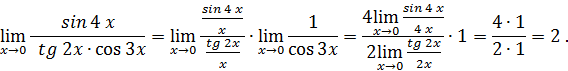
Второй замечательный придел.

 – экспонента.
– экспонента.
Следствие 1.

Пример 1.
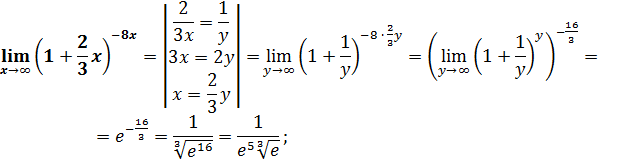
Пример 2.


Неопределенность 
Пример 1.
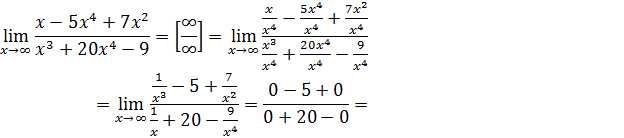
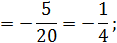
Пример 2.

Квадратный трехчлен. Неопределенность 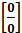
Пример 1.


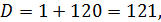





Пример 2.



ПРОИЗВОДНАЯ ФУНКЦИИ. МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.
Производной функции называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю.
Производная функции в общем виде:

Производная функции в точке x0:

Операция нахождения производной называется дифференцированием.
Пример 1.
y = C; где С = const
∆y = C – C = 0;

Пример2.


Производная степенной функции:



Механический смысл производной связан с производной от пути.
Производная от пути в некоторый момент времени равняется скорости в этот момент времени.
Sʹ(t0) = V(t0) или Sʹt = V
Sʹʹ(t0) = Vʹ(t0) = a(t0)
Пример 3.
 ,
,
t0 = 1c,
Решение:

V(t0 = 1) = 
Sʹʹ(t) = 
a(t0 = 1) = Sʹʹ (1) = 2 · 1 + 8 = 10 м/с2
Вывод:
Производная – это скорость изменения функции.
Геометрический смысл производной.

Рис.8

Значение производной функции y = f (x)в точке 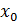 равно угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна
равно угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна 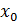 .
.
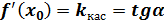
Воспользовавшись уравнением прямой  , получим уравнение касательной:
, получим уравнение касательной:

Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Из условия перпендикулярности двух прямых 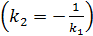 , получим уравнение нормали. Так как
, получим уравнение нормали. Так как

Тогда уравнение нормали имеет вид:

Пример 4.
Найти уравнение нормали и касательной к параболе.

Решение:






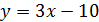 – уравнение касательной.
– уравнение касательной.




Теорема.Пусть функции  и
и  – дифференцируемы в точке x. Тогда:
– дифференцируемы в точке x. Тогда:
1) Производная суммы (разности) двух функций:

2) Производная произведения двух функций:
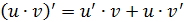
3) Производная частного двух функций:

4) Производная от переменной равна единице:

5) Производная сложной функции
Пусть 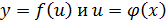 , тогда
, тогда  является сложной функцией переменной x, а переменную и называют промежуточным аргументом.
является сложной функцией переменной x, а переменную и называют промежуточным аргументом.
Сложная функция– это зависимость двух и более функций друг от друга.
Производная сложной функции находится по формуле:
 и
и 
Пример 5.



6) Производная обратной функции
Пусть функция 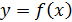 строго монотонна в интервале
строго монотонна в интервале  , тогда для нее существует обратная функция
, тогда для нее существует обратная функция  .
.
Находится по формуле:

Пример 6.

Так как 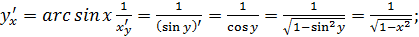

Аналогично выводятся производные других функций.
7) Производные гиперболических функций.
Гиперболические функции определяются следующими формулами:
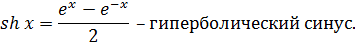



Производные гиперболические функции находятся по формулам:
1. 
2. 
3. 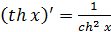
4. 
Техника дифференцирования:
Пример 1.


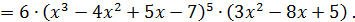
Пример2.


Пример3.

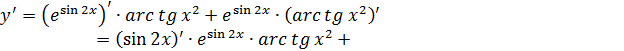

Пример4.




|
из
5.00
|
Обсуждение в статье: Бесконечно малые и бесконечно большие функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

