 |
Главная |
ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И ПРАВОЙ ЧАСТЬЮ СПЕЦИАЛЬНОГО ВИДА
|
из
5.00
|
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами:

Теорема.Общее решение неоднородного дифференциального уравнения  равняется сумме общего решения соответствующего однородного дифференциального уравненияyи частного решения неоднородного уравнения.
равняется сумме общего решения соответствующего однородного дифференциального уравненияyи частного решения неоднородного уравнения.

Для дифференциального уравнения второго порядка, у которого правая часть имеет специальный вид, применяются методы подбора формы записи частного решения  по виду
по виду  ,а затем метод неопределенных коэффициентов.
,а затем метод неопределенных коэффициентов.
Возможны следующие виды  :
:
1. Если  многочлен n ‒ й степени.
многочлен n ‒ й степени.


где  ‒ многочлен, той же степени, что и
‒ многочлен, той же степени, что и  , но с неопределенными коэффициентами (A, B, C, D…), r‒ число корней характеристического уравнения, равных нулю, то есть r= 0, или r= 1, или r= 2.
, но с неопределенными коэффициентами (A, B, C, D…), r‒ число корней характеристического уравнения, равных нулю, то есть r= 0, или r= 1, или r= 2.
Пример.

Решение:










Подставим в исходное уравнение.





2. Если правая часть уравнения  , где α ‒ любое число, тогда
, где α ‒ любое число, тогда
 , где r ‒ число корней характеристического уравнения, равных α, то есть r= 0, или r= 1, или r= 2.
, где r ‒ число корней характеристического уравнения, равных α, то есть r= 0, или r= 1, или r= 2.
В частном случае  , то
, то  , где A‒неопределенный коэффициент.
, где A‒неопределенный коэффициент.
Пример.

Решение:
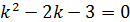


3. Если  , a и b‒ действительные числа.
, a и b‒ действительные числа.
 ,где r ‒ число корней характеристического уравнения, совпадающих с
,где r ‒ число корней характеристического уравнения, совпадающих с 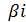 (если D< 0) и r= 0(если D≥ 0).
(если D< 0) и r= 0(если D≥ 0).
Пример.

Решение:

D= 0


Ответ:  .
.
ЧИСЛОВЫЕ РЯДЫ. СУММА РЯДА.
Задача суммирования множества слагаемых решается в теории рядов.

где u1,u2,u3…., un…–члены бесконечной числовой последовательности, называется числовым рядом.
Числа u1,u2,u3…., un… называют членами ряда, а un– общий член ряда.
Сумма конечного числа n первых членов ряда называется n–й частичной суммой ряда.
Sn= u1 + u2 +… + un,
т.е. S1= u1; S2= u1+ u2
Sn= u1+ u2+…+ un
Ряд называется сходящимся, если существует конечный предел частичной суммы Sn при n  , то есть
, то есть

Число S называется суммой ряда.
В противном случае:
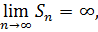
Тогда ряд называется расходящимся.
Эталонные ряды.
1. Геометрический ряд (геометрическая прогрессия)

 .
.
 .
.
Пример.


2. Гармонический ряд.

3. Обобщенный гармонический ряд.



Пример.

 .
.
Признаки сходимости знакоположительных рядов
Теорема 1. Необходимый признак сходимости.

C помощью этого признака можно установить расходимость ряда.
Пример.



Достаточные признаки
Теорема 1.Признак сравнения рядов.
Пусть даны два знакоположительных ряда:

и
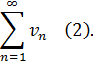
Причем  тогда, если ряд (2) сходится, то сходится и ряд (1).
тогда, если ряд (2) сходится, то сходится и ряд (1).
Если ряд (1) расходится, то расходится и ряд (2).
Пример.Исследовать ряд на сходимость:

Сравним этот ряд с геометрическим рядом:


Сравним ряды:


и так далее.
Следовательно, по признаку сравнения искомый ряд сходится.
|
из
5.00
|
Обсуждение в статье: ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И ПРАВОЙ ЧАСТЬЮ СПЕЦИАЛЬНОГО ВИДА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

