Сделать проверку решения

Задания к контрольной работе

По дисциплине «Математика» для студентов 1 курса

Направления «Менеджмент» (1 семестр)

Составил старший преподаватель кафедры ГСиЕНД Алексеева Н.А.

 

1. Общие указания. Контрольная работа должна быть выполнена в отдельной тетради в клетку с полями для пометок. Текст работы пишется разборчиво от руки чернилами одного цвета. При выполнении заданий необходимо полностью привести их условие. Задания, в которых даны лишь ответы без решений, будут считаться нерешенными. Контрольные работы другого варианта не засчитываются. Работа должна быть выполнена аккуратно, чисто, без помарок.

Контрольная работа должна быть выполнена, оформлена и сдана студентом для проверки до начала сессии.

Каждый студент выполняет свой вариант контрольной работы. Номер варианта определяется последней цифрой зачетной книжки или студенческого билета. Если последней цифрой является ноль, то выполняется десятый вариант.

 

Варианты заданий.

 

 

Задание 1

 

Пусть точка А(1; 3) – вершина квадрата АВСD, а его диагональ BD лежит на прямой х+2у-12=0. Требуется найти уравнения сторон АВ, ВС, СD и АD и координаты вершин В, С, и D. Сделать чертеж.

Решение:

 

Указание. Вспомним из школьного курса геометрии свойства диагоналей квадрата, которые будут использованы при решении этой задачи.

Диагонали квадрата: 1) взаимно перпендикулярны; 2) делятся точкой своего пересечения – центром квадрата – пополам; 3) равны.

 

Найдем уравнение прямой, на которой лежит АС – вторая диагональ квадрата. Вспомним, что уравнение любой невертикальной прямой может быть приведено к виду

,

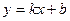где параметр k – угловой коэффициент этой прямой.

В силу свойства 1) диагоналей квадрата угловые коэффициенты и прямых АС и ВD связаны соотношением

(1)

Найдем угловой коэффициент . Для этого выразим у через х из данного уравнения прямой ВD:

, откуда . Итак, 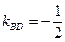. Поэтому из соотношения (1) получим, что .

Теперь уже легко найти уравнение прямой АС. Нам известны координаты ее точки А и угловой коэффициент . Используем уравнение прямой, проходящей через данную точку в данном направлении:

.

Подставим в это уравнение числовые данные нашей задачи: 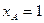, , 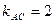.Получим: или (после упрощений)

AC:

С помощью свойства 2) диагоналей квадрата найдем координаты центра E квадрата – точки пересечения его диагоналей.

Поскольку точка E лежит на диагонали АС, ее координаты удовлетворяют уравнению прямой АС; аналогично рассуждая, получим, что координаты точки E должны одновременно удовлетворять и уравнению прямой BD. Таким образом, координаты точки E должны удовлетворять системе из уравнений прямых AC и BD

(первое – уравнение прямой АС, вторе – прямой BD). Далее, почленно вычитая второе уравнение из первого, получим: , откуда , значит х=2. Подставим найденное значение х в любое из уравнений системы, например, в первое. Найдем, что .

Итак, мы нашли координаты точки E, центра квадрата: , , т.е. E(2; 5).

Найдем длину отрезка AE – половину диагонали квадрата, а затем воспользуемся тем, что и остальные вершины квадрата находятся от его центра на таком же расстоянии Е (свойства 2) и 3) диагоналей), т.е. что все вершины квадрата лежат на окружности радиуса АЕ с центром в точке Е – рис. 1.

Подставив в правую часть этой формулы числовые значения координат точек А и Е, получим , что

.

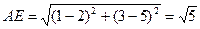Уравнение окружности радиуса АЕ с центром в точке Е записывается в виде

.

Подставив в него числовые значения радиуса АЕ и координат центра Е, получим уравнение окружности, проходящей через все вершины квадрата:

Теперь с помощью простого рассуждения находим по очереди координаты всех вершин квадрата.

Точки А и С лежат на пересечении найденной окружности и прямой АС, это общие точки указанных окружности и прямой. Значит, координаты этих точек – решения системы уравнений окружности и прямой:

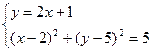
Координаты вершины А мы знаем, поэтому будем искать вершину С

Подставим во второе уравнение системы вместо у его выражение из первого уравнения. Получим:

откуда , поэтому , т.е. , значит 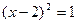. Если квадрат числа равен 1, это число равно либо 1, либо (– 1). Поэтому и тогда , либо и тогда .

Во втором случае мы получили известную нам абсциссу вершины А (а из первого уравнения системы получим ординату этой вершины), а первый случай дает нам абсциссу вершины С: . Тогда из первого уравнения системы найдем ординату вершины С: 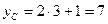. Итак, найдена вершина С(3; 7).

Аналогично, для нахождения координат вершин В и D надо решить систему, состоящую из уравнений прямой ВD и той же окружности: 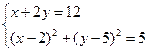. Выразим из первого уравнения х через у:

х = 12 – 2у

и подставим полученное выражение во второе уравнение системы. Получим (аналогично решению предыдущей системы 4(у – 5)² +(у – 5)² = 5, откуда либо у – 5 = 1 и тогда у = 6, либо у – 5 = – 1 и тогда у = 4.

При у = 6 первое уравнение системы дает

х = 12 – 2у = 12 – 12 = 0,

а при у = 4 аналогично получаем, что х = 4.

Итак, получены два решения системы, пары (0; 6) и (4; 4). Однако из этих решений – координаты точки В, а второе – точки D. Поскольку обе эти вершины совершенно равноправны, мы можем любую из них обозначить буквой В, тогда вторая будет вершиной D. Вся разница в том, что идут ли вершины А, В, С, D. в порядке обхода контура квадрата по или против часовой стрелки, что для решения нашей задачи безразлично; просто надо выбрать одно из этих направлений произвольно.

Мы будем считать, что вершины квадрата таковы:

В (0; 6); D(4; 4).

Нам осталось найти уравнения сторон квадрата. Для этого вспомним уравнение прямой, проходящей через точки М(х_М, y_M) и N(х_N, у_N):

(2)

и подставим в него координаты соответствующих вершин квадрата.

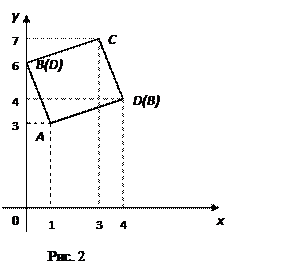Уравнение прямой АВ получим, если в формуле (2) вместо точек М и N возьмем точки А и В:

.

 

Подставляя в это уравнение координаты вершин А(1; 3) и В(0; 6), находим:

или у – 3 = – 3(х – 1), откуда у = – 3х + 6.

Аналогично получаем уравнение других сторон. Теперь можем сделать чертеж – рис. 2.

 

Ответ: В(0; 6); С(3; 7); D(4; 4);

АВ: у = – 3х + 6;

ВС: ;

СD: у = – 3х + 16;

DА: .

 

 

Варианты задания 1

 

Пусть точка А (х_А; y_А) – вершина квадрата АВСD, а его диагональ ВD расположена на прямой ах + bу + с = 0. Требуется найти уравнения сторон АВ, ВС, СD и АD и координаты вершин В, С, и D. Сделать чертеж.

Исходные данные для соответствующих вариантов задач приведены ниже.

 

 

Вариант	xА	yА	а	b	с
					-17
	-3				-16
		-2			-19
	-5	-2			-11
	-3				-13
	-7	-8
	-4				-8
	-7
	-8	-5			-2
	-5				-18

 

Задание 2

 

Найти произведение матриц А и В:

, .

 

Решение:

 

Так как сомножители имеют размеры 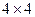и 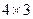, то их произведение определено и имеет размеры . Следовательно,

Варианты задания 2

 

Найти произведение матриц А и В:

, .

Вариант	k1	k2	k3
	-5		-3
			-3
	-2
			-3
			-2
		-4	-3
	-1	-2
		-4
		-5
			-3

 

 

Задание 3

 

Дана матрица А. Найти матрицу А^-1 и установить, что АА^-1=Е.

Решение:

, где

Для нахождения матрицы А^-1 необходимо, прежде всего, вычислить определитель матрицы А и убедиться в том, что она существует. Для этого воспользуемся методом Саррюса.

Вычислим алгебраические дополнения к каждому элементу матрицы по формуле:

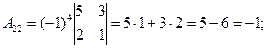
Подставим найденные значения в исходную формулу для вычисления А^-1.

.

Выполним проверку:

Проверка подтвердила правильность найденной нами матрицы.

 

Варианты задания 3

 

Дана матрица А. Найти матрицу А^-1 и установить, что АА^-1=Е.

 

Вариант	МатрицаА	Вариант	МатрицаА

 

 

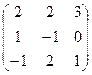
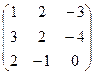
Задание 4

Найти решение системы линейных алгебраических уравнений (СЛАУ) одним из предложенных методов:

· метод Крамера

· метод обратной матрицы

· метод Гаусса

Сделать проверку решения.

Решение:

Выпишем матрицу коэффициентов системы

 

1) Решим систему методом Крамера.

Сначала рассмотрим условие совместимости, т.е.

Следовательно система совместна, т.е. имеет единственное решение.

где - получается из определителя заменой i-го столбца столбцом свободных элементов.

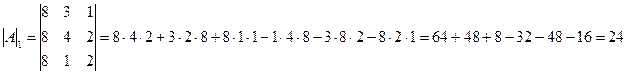
где 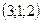- точка пересечения прямых системы.

Итак Сделаем проверку, подставив найденное решение в каждое уравнение системы.

Проверка:

; .

Итак, мы видим, что после подстановки в систему каждое уравнение обратилось в числовое тождество. Следовательно, решение системы найдено верно.

 

2) Решим систему методом обратной матрицы.

Запишем систему в матричном виде:

, , .

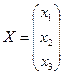; . Найдем обратную матрицу А^-1.

, где

Определитель найден в решении системы методом Крамера:

Для нахождения матрицы А^-1 осталось вычислить алгебраические дополнения к каждому элементу матрицы по формуле:

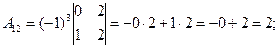
Подставим найденные значения в исходную формулу для вычисления А^-1.

.

Выполним проверку:

Проверка подтвердила правильность найденной нами матрицы.

Найдем матрицу-столбец неизвестных:

.

Ответ совпадает с решением, найденным методом Крамера, поэтому проверку делать не будем.

3) Решим систему методом Гаусса.

Поскольку элементарные преобразования системы аналогичны элементарным преобразованиям матрицы, для решения системы выпишем расширенную матрицу системы:

.

Приведем расширенную матрицу системы к эквивалентной матрице системы в ступенчатом виде.

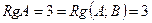- по теореме Кронекера-Капелли система имеет решение, если ранг расширенной матрицы равен рангу приведенной матрицы.

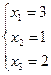
Найденный ответ совпадает с ответами, найденными предыдущими методами. Делать проверку нет необходимости, т.к. она сделана ранее.

 

 

Варианты задания 4

 

Найти решение системы линейных алгебраических уравнений (СЛАУ) одним из предложенных методов:

· метод Крамера

· метод обратной матрицы

· метод Гаусса