 |
Главная |
Лекция 9. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование. Дифференциал функции
|
из
5.00
|
Лекция 8. Линии второго порядка.
План лекции
8.1. Окружность, исследование уравнения окружности.
8.2. Вывод канонического уравнения эллипса.
8.3. Гипербола и парабола, их канонические уравнения.
8.4. Линии второго порядка. Приведение кривых второго порядка к каноническому виду.
8.5. Полярное уравнение кривой второго порядка.
8.1
Окружностьюназывается множество всех точек плоскости, равноудаленных от данной точки (центра окружности) на расстояние, равное радиусу окружности.

| |
Пусть С(а,в) – центр окружности, r – радиус окружности, M(x,y) – произвольная точка окружности (Рисунок 8.1). По определению окружности  . Выразим это равенство в координатах:
. Выразим это равенство в координатах:  . Возведем обе части в квадрат:
. Возведем обе части в квадрат:
 . (8.1)
. (8.1)
Таким образом, координаты любой точки, лежащей на окружности, удовлетворяют уравнению (8.1). Покажем, что координаты точки, не лежащей на окружности, не удовлетворяют уравнению (8.1).
Действительно, если точка М - внутри окружности, то расстояние  , т.е.
, т.е.  , а если точка M - вне окружности, то
, а если точка M - вне окружности, то  , т.е.
, т.е.  . Следовательно, уравнению (8.1) удовлетворяют координаты всех точек, лежащих на окружности, и не удовлетворяют координаты точек, не лежащих на окружности. Поэтому уравнение (81) и есть уравнение окружности.
. Следовательно, уравнению (8.1) удовлетворяют координаты всех точек, лежащих на окружности, и не удовлетворяют координаты точек, не лежащих на окружности. Поэтому уравнение (81) и есть уравнение окружности.
Если в уравнении (8.1) раскрыть скобки, то получим уравнение
 , (8.2)
, (8.2)
где  ,
,  ,
,  .
.
Если  , то уравнение (8.2) определяет окружность.
, то уравнение (8.2) определяет окружность.
Если  , то уравнение (8.2) определяет точку
, то уравнение (8.2) определяет точку  .
.
Если  , то уравнение (8.2) не имеет геометрического смысла. В этом случае говорят о мнимой окружности.
, то уравнение (8.2) не имеет геометрического смысла. В этом случае говорят о мнимой окружности.
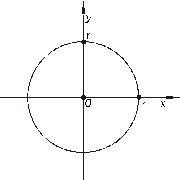
Рисунок 8.2.Окружность, имеющая
каноническое уравнение
Уравнение (8.1) можно упростить, если поместить начало новой системы координат в центр окружности (Рисунок 8.2). Тогда ее уравнение будет иметь вид:
 . (8.2)
. (8.2)
Это уравнение называется каноническим уравнением окружности, т.е. уравнением самого простого вида.
8.2
| |
Середина расстояния между фокусами называется центром эллипса, т.к. относительно этой точки эллипс симметричен.
Длина |F1F2| называется фокусным расстоянием, обозначим ее 2с, а половина этого расстояния называется полуфокусным расстоянием, оно равно с.
Примем центр эллипса за начало координат, за ось абсцисс примем прямую, проходящую через фокусы (Рисунок 8.3).

Рисунок 8.3. Эллипс
Тогда координаты фокусов будут F1(-c;0), F2(c;0). Всякий отрезок, соединяющий две точки эллипса, если он проходит через центр, называется диаметром эллипса. Наибольший диаметр проходит через фокусы, этот диаметр A1A2 называется большой осью эллипса. Длина большой оси эллипса |A1A2|=2a. Действительно, по определению эллипса |F1A2|+|F2A2|=2a, но |F1A2|=|OA2|+c, |F2A2|=|OA2|-c. Тогда получаем 2|OA2|=2a, или |OA2|=a. Аналогично |A1O|=a, следовательно, |A1A2|=2a. Число а называется большой полуосью. Наименьший диаметр эллипса перпендикулярен наибольшему, его называют малой осью эллипса и обозначают через 2b, так что |B1B2|=2b. Число b называется малой полуосью. Концы осей, т.е. точки A1,A2,B1,B2 называются вершинами эллипса. Основное свойство эллипса применимо и для вершин В1 и В2. Например, для вершины В2 получим |F1B2|+|F2B2|=2a, а т.к. |F1B2|=|F2B2|, то 2|F2B2|=2a, или |F2B2|=a. Тогда из прямоугольного ∆OF2B2 получаем важное соотношение:
 (8.4)
(8.4)
Форма эллипса при заданном а зависит только от расстояния между фокусами, т.е. от с. При сближении фокусов и при совпадении их с началом координат эллипс постепенно обратится в окружность. Наоборот, если фокусы отодвигаются от начала координат, эллипс постепенно сплющивается и вырождается в прямолинейный отрезок A1A2. Степень сжатия эллипса определяется его эксцентриситетом, который определяется дробью:
 (8.5)
(8.5)
Для эллипса эксцентриситет может изменяться от 0 до 1, причем для окружности  , для эллипса, выродившегося в прямолинейный отрезок,
, для эллипса, выродившегося в прямолинейный отрезок, 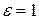 .
.
Для получения канонического уравнения эллипса возьмем произвольную точку эллипса М(x,y). Тогда по определению |MF1|+|MF2|=2a. Выразим это равенство в координатах:
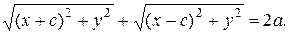 (8.6)
(8.6)
Для упрощения уравнения (8.6) придется дважды его возводить в квадрат и приводить подобные члены. В результате будет получено уравнение

или после деления на 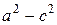 –
–

Далее учитывая, что b2=a2-c2, получаем каноническое уравнение эллипса:
 (8.7)
(8.7)
Построение эллипса, согласно его определению, можно осуществить посредством нити длиной 2а, закрепленной концами в фокусах. Зацепив нить острием карандаша, и двигая его так, чтобы нить всё время была в натянутом состоянии, мы заставим острие вычертить эллипс.
8.3
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек  и
и  , называемых фокусами, есть величина постоянная (её обозначают 2а) и меньшая расстояния между фокусами (2с).
, называемых фокусами, есть величина постоянная (её обозначают 2а) и меньшая расстояния между фокусами (2с).
Середина расстояния между фокусами называется центром гиперболы, так как относительно этой точки гипербола симметрична. Длина  - называется фокусным расстоянием, а половина этого расстояния полуфокусным расстоянием. Удобно центр гиперболы принять за начало координат, а за ось абсцисс принять прямую, проходящую через фокусы (Рисунок 8.4).
- называется фокусным расстоянием, а половина этого расстояния полуфокусным расстоянием. Удобно центр гиперболы принять за начало координат, а за ось абсцисс принять прямую, проходящую через фокусы (Рисунок 8.4).
Всякий отрезок, соединяющий две точки гиперболы и проходящий через центр, называется диаметром гиперболы. Наименьший диаметр лежит на оси абсцисс; этот диаметр  называется действительной осью гиперболы, причем
называется действительной осью гиперболы, причем  . Действительно по определению гиперболы
. Действительно по определению гиперболы 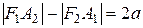 , но
, но  ,
, 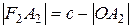 , тогда
, тогда  , или
, или  . Аналогично
. Аналогично  , следовательно,
, следовательно,  .
.
Число  называется действительной полуосью, точки
называется действительной полуосью, точки  и
и  называются вершинами гиперболы. Отношение
называются вершинами гиперболы. Отношение  называется эксцентриситетом гиперболы, причем для гиперболы
называется эксцентриситетом гиперболы, причем для гиперболы 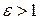 .
.

Рисунок 8.4. Гипербола
Пусть  - произвольная точка гиперболы. Тогда по определению
- произвольная точка гиперболы. Тогда по определению  , или в координатной форме
, или в координатной форме
 . (8.8)
. (8.8)
Уравнение (8.8) в результате преобразований, аналогичных проводимым при выводе уравнения эллипса, может быть сведено к виду:
 .
.
Обозначая  , получаем каноническое уравнение гиперболы:
, получаем каноническое уравнение гиперболы:
 . (8.9)
. (8.9)
Прямые  являются асимптотами гиперболы. Это прямые, к которым гипербола приближается в бесконечности, но не пересекает их. С геометрической точки зрения
являются асимптотами гиперболы. Это прямые, к которым гипербола приближается в бесконечности, но не пересекает их. С геометрической точки зрения  - ордината асимптоты, восстановленной из вершины гиперболы. Для построения асимптот гиперболы целесообразно предварительно построить прямоугольник со сторонами
- ордината асимптоты, восстановленной из вершины гиперболы. Для построения асимптот гиперболы целесообразно предварительно построить прямоугольник со сторонами  и
и  , параллельными координатным осям и с центром в начале координат (такой прямоугольник называется основным прямоугольником гиперболы). Точки
, параллельными координатным осям и с центром в начале координат (такой прямоугольник называется основным прямоугольником гиперболы). Точки  и
и  определяют мнимую ось гиперболы
определяют мнимую ось гиперболы  .
.
Если в уравнении (8.9)  , то гипербола называется равнобочной. Ее асимптоты
, то гипербола называется равнобочной. Ее асимптоты  образуют прямой угол. Если за оси принять асимптоты, то уравнение примет вид
образуют прямой угол. Если за оси принять асимптоты, то уравнение примет вид  . Таким образом, равнобочная гипербола является графиком обратной пропорциональности.
. Таким образом, равнобочная гипербола является графиком обратной пропорциональности.
Заметим, что уравнение
 (8.10)
(8.10)
тоже определяет гиперболу, у которой действительная ось расположена на оси  , а мнимая ось – на оси
, а мнимая ось – на оси  .
.
Параболой называется множество всех точек плоскости, равноудаленных от данной точки  (называемой фокусом параболы) и от данной прямой (называемой директрисойпараболы).
(называемой фокусом параболы) и от данной прямой (называемой директрисойпараболы).
Для вывода канонического уравнения параболы проведем ось  прямоугольной системы координат через фокус
прямоугольной системы координат через фокус  перпендикулярно директрисе, начало координат
перпендикулярно директрисе, начало координат  поместим на равных расстояниях от фокуса и директрисы (Рисунок 8.5). Расстояние от фокуса до директрисы обозначим через
поместим на равных расстояниях от фокуса и директрисы (Рисунок 8.5). Расстояние от фокуса до директрисы обозначим через  (оно называется параметром параболы). Тогда
(оно называется параметром параболы). Тогда  , а директриса задается уравнением
, а директриса задается уравнением  . Пусть
. Пусть  - произвольная точка параболы. Опустим перпендикуляр
- произвольная точка параболы. Опустим перпендикуляр  на директрису
на директрису  . Тогда по определению
. Тогда по определению  . Выразим это условие в координатах:
. Выразим это условие в координатах:
 .
.

Рисунок 8.5. Парабола.
Возводя в квадрат и приводя подобные, получаем каноническое уравнение параболы:
 . (8.11)
. (8.11)
Вершинойпараболы называется точка пересечения параболы с ее осью симметрии. Ось симметрии параболы называется осью параболы. Парабола, определяемая уравнением (8.11), имеет ось, совпадающую с осью  .
.
Заметим, что уравнение  определяет параболу, симметричную относительно оси
определяет параболу, симметричную относительно оси  .
.
8.4
Между эллипсом, гиперболой и параболой имеется близкое родство. Это объясняется тем, что все они - линии второго порядка. Все эти линии могут быть получены при пересечении прямого кругового конуса с плоскостью, поворачивающейся вокруг оси, выбранной, например, перпендикулярно к оси конуса (Рисунок 8.6). Пока наклон мал, в сечении получается эллипс. При увеличении наклона эллипс удлиняется, его эксцентриситет растет. Когда плоскость наклонена к оси конуса так же, как образующие, в сечении получается парабола. Наконец, когда плоскость будет пересекать обе половины конуса, в сечении будет гипербола. По этой причине эллипс, гиперболу и параболу иногда называют коническими сечениями.

Рисунок 8.6. Родство кривых второго порядка.
Родство между указанными линиями обусловлено тем, что все они задаются уравнением второй степени, а поэтому и носят общее название линий(или кривых) второго порядка.
Общим уравнением линий второго порядканазывается уравнение вида
 . (8.12)
. (8.12)
Путем преобразования координат это уравнение можно привести к каноническому виду. Осуществим поворот осей координат на угол 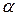 по формулам:
по формулам:
 (8.13)
(8.13)
Угол 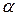 выберем таким, чтобы получилось уравнение, не содержащее произведение координат. Для этого подставляем (8.13) в (8.12) и приравниваем коэффициент при
выберем таким, чтобы получилось уравнение, не содержащее произведение координат. Для этого подставляем (8.13) в (8.12) и приравниваем коэффициент при  к
к  . В результате получаем уравнение для определения угла поворота:
. В результате получаем уравнение для определения угла поворота:
 , (8.14)
, (8.14)
откуда

или
 . (8.15)
. (8.15)
Формула (8.15) определяет 4 возможных значения для  любое из которых позволяет привести уравнение (8.12) к виду:
любое из которых позволяет привести уравнение (8.12) к виду:
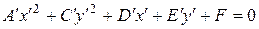 (8.16)
(8.16)
Если  , то уравнение (8.16) может быть приведено к виду:
, то уравнение (8.16) может быть приведено к виду:
 , (8.17)
, (8.17)
которое с помощью параллельного переноса начала координат
 (8.18)
(8.18)
сводится к каноническому виду.
Если  , т.е.
, т.е.  или
или  , то уравнение (8.16) может быть приведено к виду:
, то уравнение (8.16) может быть приведено к виду:
 , (8.19)
, (8.19)
или
 . (8.20)
. (8.20)
Применяя параллельный перенос (8.18), где  или
или  , уравнения (8.19) или (8.20) сводятся к каноническому виду.
, уравнения (8.19) или (8.20) сводятся к каноническому виду.
Заметим, что при любом повороте осей координат (8.13), хотя координаты  при членах второй степени, вообще говоря, меняются, выражение
при членах второй степени, вообще говоря, меняются, выражение  при этом остается инвариантным (т.е. неизменным). Таким образом,
при этом остается инвариантным (т.е. неизменным). Таким образом,  . По знаку этого выражения можно определить вид кривой.
. По знаку этого выражения можно определить вид кривой.
1. Если  , то уравнение (8.12) задает эллипс
, то уравнение (8.12) задает эллипс  , точку
, точку  , или мнимый эллипс
, или мнимый эллипс  , иначе говоря, кривую эллиптического типа.
, иначе говоря, кривую эллиптического типа.
2. Если  , то уравнение (8.12) задает гиперболу
, то уравнение (8.12) задает гиперболу  , или пару пересекающихся прямых
, или пару пересекающихся прямых  , иначе говоря, кривую гиперболического типа.
, иначе говоря, кривую гиперболического типа.
3. Если  , то уравнение (8.12) задает параболу
, то уравнение (8.12) задает параболу  или
или  , пару параллельных или совпадающих прямых (
, пару параллельных или совпадающих прямых (  или
или  ) или мнимую кривую (
) или мнимую кривую ( 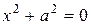 или
или  ), иначе говоря, кривую параболического типа.
), иначе говоря, кривую параболического типа.
8.5
Выведем полярное уравнение линии второго порядка на примере эллипса.

Рисунок 8.7. Полярное уравнение эллипса
Поместим полюс  полярной системы координат в правый фокус эллипса (точка
полярной системы координат в правый фокус эллипса (точка  ), расположив полярную ось на положительной части оси
), расположив полярную ось на положительной части оси  (Рисунок 8.7). Пусть
(Рисунок 8.7). Пусть  - произвольная точка эллипса. По теореме косинусов из
- произвольная точка эллипса. По теореме косинусов из  имеем
имеем
 .
.
Учитывая, что  ,
,  ,
,  ,
,  , получаем
, получаем  .
.
Откуда, заменяя 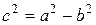 , получим:
, получим:
 .
.
Обозначим  и назовем эту величину параметром эллипса,
и назовем эту величину параметром эллипса,  - эксцентриситет.
- эксцентриситет.
Тогда
 – (8.21)
– (8.21)
полярное уравнение эллипса.
Если поместить полюс в левый фокус эллипса, то полярное уравнение будет иметь вид
 . (8.22)
. (8.22)
Заметим, что уравнения (8.21) и (8.22) являются полярными уравнениями любой кривой второго порядка, его вид определяется величиной эксцентриситета. Если  , то кривая эллиптического типа. Если
, то кривая эллиптического типа. Если 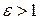 , то кривая гиперболического типа. При
, то кривая гиперболического типа. При  – кривая параболического типа.
– кривая параболического типа.
Лекция 9. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование. Дифференциал функции.
План лекции
9.1. Функции заданные неявно, их дифференцирование.
9.2. Параметрически заданные функции и их дифференцирование.
9.3. Логарифмическое дифференцирование.
9.4. Дифференциал функции, определение и свойства.
9.1
Пусть значения двух переменных  и
и  связаны между собой некоторым уравнением
связаны между собой некоторым уравнением
 . (9.1)
. (9.1)
Если функция  , определенная на некотором интервале
, определенная на некотором интервале  , такова, что уравнение (9.1) при подстановке в него вместо
, такова, что уравнение (9.1) при подстановке в него вместо  выражения
выражения  обращается в тождество относительно
обращается в тождество относительно  , то функция
, то функция  есть неявная функция, определенная уравнением (9.1).
есть неявная функция, определенная уравнением (9.1).
Так, например, уравнение  неявно определяет следующие элементарные функции:
неявно определяет следующие элементарные функции:  и
и  , которые определяют соответственно верхнюю и нижнюю половину окружности, радиус которой равен
, которые определяют соответственно верхнюю и нижнюю половину окружности, радиус которой равен  . Аналогично, уравнения
. Аналогично, уравнения  ,
,  ,
,  ,
,  , задающие некоторые кривые второго порядка (читатель может определить вид кривой второго порядка самостоятельно), являются неявно заданными функциями.
, задающие некоторые кривые второго порядка (читатель может определить вид кривой второго порядка самостоятельно), являются неявно заданными функциями.
Но не всякую неявно заданную функцию можно представить явно в виде  , где
, где  - элементарная функция. Так, например, функции
- элементарная функция. Так, например, функции  ,
,  нельзя разрешить относительно
нельзя разрешить относительно  , а уравнение
, а уравнение  нельзя разрешить ни относительно
нельзя разрешить ни относительно 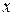 , ни относительно
, ни относительно  .
.
Поэтому необходимо указать способ отыскания производной неявно заданной функции.
Если  есть неявная функция от
есть неявная функция от  , то есть задана уравнением
, то есть задана уравнением  , неразрешенным относительно
, неразрешенным относительно  , то для нахождения производной
, то для нахождения производной  нужно продифференцировать по
нужно продифференцировать по  обе части равенства, помня, что
обе части равенства, помня, что  есть функция от
есть функция от  , и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от
, и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от  и
и  , т.е.
, т.е.  .
.
Вторую производную  от неявной функции получаем, дифференцируя функцию
от неявной функции получаем, дифференцируя функцию  по переменной
по переменной  , помня, что
, помня, что  - функция от
- функция от 
 .
.
Заменяя  через
через  получаем
получаем  и т.д.
и т.д.
Для нахождения производных более высоких порядков этот процесс продолжаем. Для нахождения значения производной неявной функции при данном значении аргумента  нужно знать и значение функции
нужно знать и значение функции  при данном значении
при данном значении  .
.
Пример 1. Найти производную функции  , заданной неявно.
, заданной неявно.
Решение. Дифференцируем обе части уравнения, считая  функцией аргумента
функцией аргумента  :
: 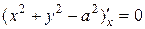 ,
,  , тогда
, тогда  .
.
Заметим, что если бы стали дифференцировать соответствующую явную функцию  , то получили бы тот же результат:
, то получили бы тот же результат:
 .
.
Пример 2. Найти производную второго порядка для функции  .
.
Решение. Дифференцируем по  , считая
, считая  . Получаем
. Получаем  ,
,  , отсюда
, отсюда  .
.
Дифференцируем вновь по  , получаем
, получаем
 . Подставляем вместо
. Подставляем вместо  его выражение
его выражение
 .
.
Если учесть, что из уравнения эллипса следует, что  , то окончательно
, то окончательно  .
.
9.2
Если даны два уравнения
 , (9.2)
, (9.2)
где  принимает значения, содержащиеся на отрезке
принимает значения, содержащиеся на отрезке  , то каждому значению
, то каждому значению  соответствуют значения
соответствуют значения  и
и  (функции
(функции  и
и  предполагаем однозначными). Если рассматривать значения
предполагаем однозначными). Если рассматривать значения  и
и  как координаты точки на координатной плоскости Оxy, то каждому значению
как координаты точки на координатной плоскости Оxy, то каждому значению  будет соответствовать определенная точка плоскости. Когда
будет соответствовать определенная точка плоскости. Когда  изменяется от
изменяется от  до
до  , эта точка на плоскости описывает некоторую кривую.
, эта точка на плоскости описывает некоторую кривую.
Уравнения (9.2) называются параметрическими уравнениями кривой,  - параметром, а способ задания кривой уравнениями (9.2) – параметрическим.
- параметром, а способ задания кривой уравнениями (9.2) – параметрическим.
Предположим, что функция  имеет обратную
имеет обратную  , тогда, очевидно,
, тогда, очевидно,  является функцией от
является функцией от  :
:
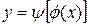 . (9.3)
. (9.3)
Таким образом, уравнения (9.2) определяют  как функцию от
как функцию от  , и говорят, что функция
, и говорят, что функция  от
от  задается параметрически.
задается параметрически.
Укажем правило для вычисления производной параметрически заданной функции. Предположим, что функции  и
и  имеют производные, обратная функция
имеют производные, обратная функция  также имеет производную. Тогда определенную параметрическими уравнениями функцию
также имеет производную. Тогда определенную параметрическими уравнениями функцию  можно рассматривать как сложную функцию
можно рассматривать как сложную функцию 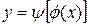 . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции
 (9.4)
(9.4)
На основании теоремы о дифференцировании обратной функции  . Подставляя последнее выражение в (9.4), получаем
. Подставляя последнее выражение в (9.4), получаем
 . (9.5)
. (9.5)
Выведенная формула дает возможность находить производную  от функции, заданной параметрически, не находя выражения непосредственной зависимости
от функции, заданной параметрически, не находя выражения непосредственной зависимости  от
от  . Для нахождения второй производной
. Для нахождения второй производной  дифференцируем по
дифференцируем по  равенство (9.5), имея ввиду, что
равенство (9.5), имея ввиду, что  есть функция от
есть функция от  . Тогда
. Тогда  . Таким образом, получили формулу вычисления производной второго порядка для функции заданной параметрически
. Таким образом, получили формулу вычисления производной второго порядка для функции заданной параметрически
 . (9.6)
. (9.6)
Пример 3. Найти производные  и
и 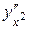 для функции, заданной параметрическими уравнениями
для функции, заданной параметрическими уравнениями 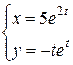 .
.
Решение. Вычисляем  ,
,  .
.
Тогда 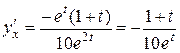 ,
,
 .
.
9.3
Дифференцирование многих функций значительно упрощается, если их предварительно прологарифмировать. Использование логарифмирования при нахождении производной носит название логарифмического дифференцирования. Суть его состоит в следующем.
Если требуется найти производную  из уравнения
из уравнения  , то можно
, то можно
1. Прологарифмировать обе части уравнения  , т.е. найти
, т.е. найти  .
.
2. Найти логарифмическую производную  .
.
3. Записать производную искомой функции по формуле
 .
.
4. При необходимости провести алгебраические преобразования.
Логарифмическое дифференцирование полезно применять, когда заданная функция содержит логарифмирующиеся операции (умножение, деление, возведение в степень, извлечение корня), и в частности, для нахождения производной от показательно-степенной функции  , где
, где 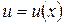 ,
,  .
.
Пример 4. С помощью логарифмического дифференцирования, вычислить производную функции  .
.
Решение. Прологарифмируем данную функцию
 .
.
Находим логарифмическую производную

 .
.
Записываем производную данной функции и проводим алгебраические преобразования
 .
.
9.4
Пусть функция  дифференцируема на отрезке
дифференцируема на отрезке  . По определению производной в некоторой точке
. По определению производной в некоторой точке 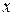 на отрезке
на отрезке  имеем
имеем  . С учетом условия существования предела
. С учетом условия существования предела
 , (9.7)
, (9.7)
где  - бесконечно малая величина.
- бесконечно малая величина.
Умножим (9.7) на 
 .(9.8)
.(9.8)
Пусть  . Тогда
. Тогда 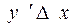 линейно по
линейно по  , так как
, так как  не зависит от
не зависит от  . При
. При  ,
,  - бесконечно малая величина, но более низкого порядка чем
- бесконечно малая величина, но более низкого порядка чем  , т.к.
, т.к.  .
.
Поэтому  - является главной частью приращения функции, или эту величину ещё называют дифференциалом функции и обозначают
- является главной частью приращения функции, или эту величину ещё называют дифференциалом функции и обозначают  .
.

Заметим, что дифференциал функции независимой переменной, равен её приращению, т.е.  . Тогда сам дифференциал функции
. Тогда сам дифференциал функции  можно записать в виде
можно записать в виде  . Заметим, что отсюда и существует обозначение производной
. Заметим, что отсюда и существует обозначение производной  .
.
Рассмотрим геометрический смысл дифференциала функции (Рисунок 9.1). На рисунке величина отрезка  - приращение аргумента, которое придали функции в точке
- приращение аргумента, которое придали функции в точке 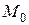 ,
,  - приращение функции, вызванное приращением аргумента
- приращение функции, вызванное приращением аргумента  . Касательная к графику функции в точке
. Касательная к графику функции в точке 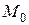 отсекает от приращения функции отрезок
отсекает от приращения функции отрезок  . Из прямоугольного треугольника
. Из прямоугольного треугольника  катет
катет  . Учитывая геометрический смысл производной,
. Учитывая геометрический смысл производной,  , где угол
, где угол 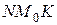 - угол нак
- угол нак
|
из
5.00
|
Обсуждение в статье: Лекция 9. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование. Дифференциал функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

