 |
Главная |
Учитывая замечание в п. 1.2.1 об использовании функции Хевисайда для записи оригиналов, соотношение (3.12) можно записать в виде
|
из
5.00
|
 . (3.12 а)
. (3.12 а)
Теорема запаздывания является удобным способом для нахождения изображений кусочно-непрерывных функций, которыми, как правило, описываются импульсные процессы. Часто встречающиеся в технических приложениях кусочно-непрерывные и периодические функции имеют различные аналитические выражения в различных промежутках значений аргумента; с помощью функции Хевисайда они могут быть записаны единым аналитическим выражением, после чего успешно применяется теорема запаздывания для получения изображений ступенчатых и периодических функций.
Пример 3.3. Найти изображение импульса
 Рис.3.2
Рис.3.2
|  действующего в течение промежутка времени
действующего в течение промежутка времени  . График его изображен на рис. 3.2. . График его изображен на рис. 3.2.
|
Решение. С помощью функции Хевисайда данную функцию можно записать единым аналитическим выражением
 .
.
Воспользовавшись соответствием  и теоремой смещения, найдем
и теоремой смещения, найдем  . И, наконец, по свойству линейности получаем
. И, наконец, по свойству линейности получаем
 .
.
3.2. Дифференцирование и интегрирование оригиналов
Рассмотрим правила отображения операций дифференцирования и интегрирования оригиналов. Следующая теорема устанавливает связь между производными оригинала и его изображением.
Теорема дифференцирования оригинала.Если  непрерывно дифференцируема на
непрерывно дифференцируема на  и
и  является оригиналом, то из
является оригиналом, то из  следует:
следует:
 , (3.13)
, (3.13)
т.е. дифференцирование оригинала сводится к умножению его изображения на параметр 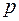 и вычитанию
и вычитанию  , где под
, где под  следует понимать |
следует понимать | 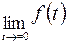 .
.
Доказательство.Найдем преобразование Лапласа для 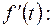


Проинтегрируем по частям, помня, что в точке  функция
функция  может иметь разрыв первого рода. Положим
может иметь разрыв первого рода. Положим  тогда
тогда  и
и
 .
.
Значение первого слагаемого зависит от поведения  при
при  и
и  . В процессе доказательства теоремы существования изображения была получена оценка
. В процессе доказательства теоремы существования изображения была получена оценка

где 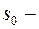 показатель роста оригинала
показатель роста оригинала  . При условии
. При условии  . Следовательно, когда
. Следовательно, когда 
 Оригинал
Оригинал  в точке
в точке  является либо непрерывной функцией и тогда
является либо непрерывной функцией и тогда  так как, по определению
так как, по определению 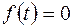 при
при  , либо имеет разрыв первого рода и тогда существует конечный правый предел, т.е.
, либо имеет разрыв первого рода и тогда существует конечный правый предел, т.е.
 .
.
Следовательно,  .
.
Итак, окончательно получаем

 .
.
В частности, когда 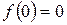 ,
,
 (3.13 а)
(3.13 а)
Применим правило (3.13) ко второй производной  предполагая, что производные любого порядка оригинала существуют и являются оригиналами.
предполагая, что производные любого порядка оригинала существуют и являются оригиналами.

Так же найдем

Применив правило (3.13)  раз, найдем
раз, найдем

где 
Таким образом, получено обобщенное правило соответствия для производной любого порядка оригинала :
 . (3.14)
. (3.14)
Если  то формула – соответствие (3.14) приобретает простой вид
то формула – соответствие (3.14) приобретает простой вид
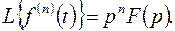 (3.14 а)
(3.14 а)
Пример 3.4. Найти изображение функции  если известно
если известно  '
'
Решение. Используя (3.13а), получим
 ,
,
Что совпадает с полученным ранее результатом (3.3).
|
из
5.00
|
Обсуждение в статье: Учитывая замечание в п. 1.2.1 об использовании функции Хевисайда для записи оригиналов, соотношение (3.12) можно записать в виде |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

