 |
Главная |
Удаление левой рекурсии
|
из
5.00
|
Классификация формальных грамматик по Хомскому
· Грамматика типа 0 (общего вида). Правила имеют вид α→β
· Грамматика типа 1 (контекстно зависимая, КЗ)
Правила имеют вид αAβ → αγβ. γ принадлежит V+, т.е. грамматика является неукорачивающей
α,β называются левым и правым контекстом
· Грамматика типа 2 (контекстно свободная, КС)
Правила имеют вид A → α. α принадлежит V*, т.е. грамматика может быть укорачивающей => КС языки не содержатся в КЗ
Наиболее близкая к БНФ
· Грамматика типа 3 (автоматная, регулярная)
Правила имеют вид A → aB, A → a, A → ε
Автоматные языки содержатся в КС языках
Пример. Грамматика, порождающая язык правильных скобочных выражений.
S → (S) | SS | ε
Порождение (вывод)
Обозначения
=>
=>+ (1 или более)
=>* (0 или более)
Сентенциальная форма грамматики- это строка, которая может быть выведена из стартового символа.
Предложение (сентенция) грамматики- это сентенциальная форма, состоящая из одних терминалов.
Язык L(G) грамматики- это множество всех ее предложений.
Обозначения:
=>(lm)
=>(lm)*
=>(rm)+
Левый, правый вывод (порождение).
Пример
E → E + T
| T
T → T * P
| P
P → i
| ( E )
Левый и правый вывод для предложения i + i * i
Дерево вывода (синтаксическое дерево, дерево разбора) строки предложения. В отличие от порождения, из него исключена информация о порядке вывода.
Крона дерева разбора - цепочка меток листьев слева направо
Грамматика, которая дает более одного дерева разбора для некоторого предложения, называется неоднозначной.
Пример неоднозначной грамматики. Грамматика арифметических выражений.
E → E+E | E*E | i
Два дерева разбора для цепочки i + i * i
Преобразование в эквивалентную однозначную грамматику:
E → E + T
| T
T → T * P
| P
P → i
Пример неоднозначной грамматики. Грамматика условного оператора
S → if b then S
| if b then S else S
| a
Два дерева разбора для цепочки if b then if b then a
Преобразование в эквивалентную однозначную грамматику:
S → if b then S
| if b then S2 else S
| a
S2 → if b then S2 else S2
| a
44.Формальные языки и грамматики: непустые, конечные и бесконечные языки


45.Эквивалентность и минимизация автоматов
Эквивалентность конечных автоматов
Пусть S - алфавит (конечное множество символов) и S* - множество всех слов в алфавите S. Будем обозначать буквой eпустое слово, т.е. вовсе не содержащее букв (символов из S), а знаком × - операцию приписывания (конкатенации) слов.
Так, аав × ва = аавва. Знак × операции приписывания часто опускают.
Слова в алфавите S будем обозначать малыми греческими буквами a, b, g, .... Очевидно, e является единицей для операции приписывания:
ae = ea = a.
Очевидно также, что операция приписывания ассоциативна, т.е. (ab)g = a(bg).
Таким образом, множество S* всех слов в алфавите S относительно операции приписывания является полугруппой с единицей, т.е. моноидом;
S* называют свободным моноидом над алфавитом S.
Минимизация конечного автомата
Разные конечные автоматы могут функционировать одинаково, даже если у них разное число состояний. Важной задачей является нахождение минимального конечного автомата, который реализует заданное автоматное отображение [3].
Эквивалентными естественно назвать два состояния автомата, которые нельзя различить никакими входными словами.
Определение 1: Два состояния р и q конечного автомата
А = (S,X,Y,s0,d,l) называются эквивалентными (обозначается p~q), если ("aÎ X*)l*(p,a) =l*(q, a)
46.Эквивалентность одноленточных и многоленточных машин Тьюринга
Очевидно, что понятие k–ленточной МТ шире, чем понятие «обычной» одноленточной машины. ОПРЕДЕЛЕНИЕ 6. (k+1)–ленточная МТ M′ с программой w симулирует k–ленточную машину M, если для любого набора входных слов (x1, x2, …, xk) результат работы M′ совпадает с результатом работы M на этих же входных данных. Предполагается, что вначале слово w записано на (k+1)-й ленте M′. Под результатом понимается состояние первых k лент МТ в момент остановки, а если на данном входе M не останавливается, то симулирующая ее машина также не должна останавливаться на данном входе.
ОПРЕДЕЛЕНИЕ 7. (k+1)–ленточная МТ M* называется универсальной машиной Тьюринга для k–ленточных машин, если для любой k- ленточной машины M существует программа w, на которой M* симулирует M. 12 Обратите внимание: в определении универсальной МТ одна и та же машина M′ должна симулировать разные k-ленточные машины (на разных программах w). Рассмотрим следующую теорему [8]. ТЕОРЕМА 3. Для любого k≥1 существует универсальная (k+1)– ленточная машина Тьюринга. Доказательство. Теорему докажем конструктивно, т.е. покажем, как можно построить требуемую универсальную машину M*. Рассмотрим лишь общую схему построения, опустив сложные детали. Основная идея заключается в том, чтобы на дополнительную (k+1)-ю ленту разместить описание симулируемой машины Тьюринга и использовать это описание в процессе симулирования.
ОПРЕДЕЛЕНИЕ 8. Будем говорить, что машина Тьюринга M вычисляет частичную функцию f:A*→A*, если для любого x∈A*, записанного на первую ленту машины M: • если f(x) определено, то M останавливается, и в момент остановки на последней ленте машины записано слово f(x); • если f(x) не определено, то машина M не останавливается.
ОПРЕДЕЛЕНИЕ 9. Будем говорить, что машины M и M′ эквивалентны, если они вычисляют одну и ту же функцию. Понятие эквивалентности «слабее», чем симулирование: если машина M′ симулирует машину M, то машина M′ эквивалентна M; обратное, вообще говоря, неверно. С другой стороны, для симулирования требуется, чтобы у M′ было как минимум столько же лент, сколько и у M, в то время как для эквивалентности это не 15 обязательно. Именно это свойство позволяет нам сформулировать и доказать следующую теорему [8].
ТЕОРЕМА 4. Для любой k-ленточной машины M, имеющей временную сложность T(n), существует эквивалентная ей одноленточная машина M′ с временной сложностью T′ (n) = O(T 2 (n)).
48.Эквивалентные преобразования КС-грамматик: исключение цепных правил, удаление произвольного правила грамматики
Определение. Правило грамматики вида <A>  <B>, где <A>, <B>
<B>, где <A>, <B> 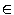 VA, называется цепным.
VA, называется цепным.
Утверждение. Для КС-грамматики Г, содержащей цепные правила , можно построить эквивалентную ей грамматику Г', не содержащую цепных правил.
Идея доказательства заключается в следующем. Если схема грамматики имеет вид
R = {...,<A>  <B>,...,<B>
<B>,...,<B>  <C>, ... , <C>
<C>, ... , <C>  a<X> },
a<X> },
то такая грамматика эквивалентна грамматике со схемой
R' = {...,<A>  a<X>,...},
a<X>,...},
поскольку вывод в грамматике со схемой R цепочки a<X>:
<A> 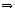 <B>
<B> 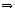 <C>
<C> 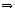 a<X>
a<X>
может быть получен в грамматике со схемой R' с помощью правила <A>  a<X>.
a<X>.
В общем случае доказательство последнего утверждения можно выполнить так. Разобьем R на два подмножества R1 и R2, включая в R1 все правила вида
<A>  <B>
<B>
Для каждого правила из R1 найдем множество правил S(<Ai>), которые строятся так:
если <Ai> 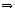 *<Aj> и в R2 есть правило <Aj>
*<Aj> и в R2 есть правило <Aj>  α, где α - цепочка словаря (Vт
α, где α - цепочка словаря (Vт 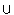 VA)*, то в S(<Ai>) включим правило <Ai>
VA)*, то в S(<Ai>) включим правило <Ai>  α.
α.
Построим новую схему R' путем объединения правил R2 и всех построенных множеств S(<Ai>). Получим грамматику Г' = {Vт, VA, I, R'}, которая эквивалентна заданной и не содержит правил вида <A>  <B>.
<B>.
В качестве примера выполним исключение цепных правил из грамматики Г1.9 со схемой:
Г1.9:
R={<E>  <E>+<T>|<T>,
<E>+<T>|<T>,
<T>  <T>*<F>|<F>,
<T>*<F>|<F>,
<F>  (<E>)|a }
(<E>)|a }
Вначале разобьем правила грамматики на два подмножества:
R1 = { <E>  <T>,<T>
<T>,<T>  <F> },
<F> },
R2 = { <E>  <E>+<T>, <T>
<E>+<T>, <T>  <T>*<F>, <F>
<T>*<F>, <F>  (<E>)|a }
(<E>)|a }
Для каждого правила из R1 построим соответствующее подмножество.
S(<E>) = { <E>  <T>*<F>, <E>
<T>*<F>, <E>  (<E>)|a },
(<E>)|a },
S(<T>) = { <T>  (<E>)|a}
(<E>)|a}
В результате получаем искомую схему грамматики без цепных правил в виде:
R2 U S(<E>) U S(<T>) = { <E>  <T>+<T> | <T>*<F> | (<E>) | a,
<T>+<T> | <T>*<F> | (<E>) | a,
<T>  <T>*<F> | (<E>) | a,
<T>*<F> | (<E>) | a,
<F>  (<E>) | a }
(<E>) | a }
Последний вид рассматриваемых преобразований связан с удалением из грамматики правил с пустой правой частью.
Определение. Правило вида <A>  $ называется аннулирующим правилом.
$ называется аннулирующим правилом.
49.Эквивалентные преобразования КС-грамматик: удаление бесполезных символов.
Пусть дана произвольная КС-грамматика G. Нетерминал A этой грамматики называется продуктивным, если существует такая терминальная цепочка (в том числе и пустая), что A Þ*a. В противном случае нетерминал называется непродуктивным.
Теорема. Каждая КС-грамматика эквивалентна КС-грамматике без непродуктивных нетерминалов.
Нетерминал A грамматики G называется достижимым, если существует такая цепочка a, что S Þ*a. В противном случае нетерминал называется недостижимым.
Теорема. Каждая КС-грамматика эквивалентна КС-грамматике без недостижимых нетерминалов.
Нетерминальный символ в КС-грамматике называется бесполезным (или лишним), если он либо недостижим, либо непродуктивен.
Теорема. Каждая КС-грамматика эквивалентна КС-грамматике, в которой нет бесполезных нетерминалов.
Пример. Устраним бесполезные символы в грамматике
S ® aC | A; A® cAB; B® b ; C® a .
Шаг 1. Строим множество достижимых символов: {S} ® {S, C, A}® {S, C, A, B}.Все нетерминалы достижимы. Недостижимых нет грамматика не меняется.
Шаг 2. Строим множество продуктивных символов: { C, B}® {S, C, B}.Получаем, что A— не продуктивен. Выкидываем его и все правила с ним из грамматики. Получим
S ® aC ; B® b ; C® a .
Шаг 3. Строим множество достижимых символов новой грамматики: {S} ® {S, C}.Получаем, что B недостижим. Выкидываем его и все правила с ним из грамматики. Получим
S ® aC ; C® a .
Это — окончательный результат.
50. Эквивалентные преобразования КС-грамматик: устранение левой рекурсии, левая факторизация
Удаление левой рекурсии
Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии. Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.
Непосредственную левую рекурсию, то есть рекурсию вида  , можно удалить следующим способом. Сначала группируем A -правила:
, можно удалить следующим способом. Сначала группируем A -правила:
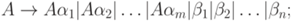
где никакая из строк 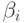 не начинается с A. Затем заменяем этот набор правил на
не начинается с A. Затем заменяем этот набор правил на

где A' - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии. С помощью этой процедуры удаляются все непосредственные левые рекурсии, но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.
Левая факторизация
Oсновная идея левой факторизации в том, что в том случае, когда неясно, какую из двух альтернатив надо использовать для развертки нетерминала A, нужно изменить A -правила так, чтобы отложить решение до тех пор, пока не будет достаточно информации для принятия правильного решения.
Если 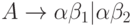 - два A -правила и входная цепочка начинается с непустой строки, выводимой из
- два A -правила и входная цепочка начинается с непустой строки, выводимой из 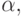 мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув
мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув 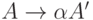 . Тогда после анализа того, что выводимо из
. Тогда после анализа того, что выводимо из 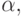 можно развернуть по
можно развернуть по  или по
или по  . Левофакторизованные правила принимают вид
. Левофакторизованные правила принимают вид
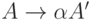
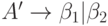
51.Язык машины Тьюринга.
В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особыйпустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
|
из
5.00
|
Обсуждение в статье: Удаление левой рекурсии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

