 |
Главная |
Представление систем с помощью графов
|
из
5.00
|
Граф G на множестве вершин X и множестве друг U.
G(X,U)
Uij=(xi,xj), 
Дуга Uj исходя из xi и заходит в xj. Такая дуга становится инцидентной вершинам xi и xj.
Если взять две вершины  , и x<y, то вершина Х предшествует вершине Y, следовательно y следует за x.
, и x<y, то вершина Х предшествует вершине Y, следовательно y следует за x.
Если записано x≤y следовательно x=y или из вершины x в y существует путь.
Дуги называются смежными, если они различны, но имеют 1 общую вершину. Вершины смежные, если они различны и существует дуга из одной вершины в другую.
Некая вершина  , которая следует за всеми вершинами подмножества Y множества X называется мажорантой (стоком). Может существовать несколько мажорант.
, которая следует за всеми вершинами подмножества Y множества X называется мажорантой (стоком). Может существовать несколько мажорант.
Вершина  , которая предшествует всем вершинам подмножества Y множества X называется минорантой (истоком). Может существовать несколько минорант.
, которая предшествует всем вершинам подмножества Y множества X называется минорантой (истоком). Может существовать несколько минорант.
Для неориентированного графа вводится понятие: локальная степень вершины X – число ребер инцидентных вершине x.
Обозначается: 
Если  четно, то вершина тоже и наоборот.
четно, то вершина тоже и наоборот.
Граф называется однородным степени n, если локальная степень всех вершин  для любого
для любого 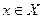 .
.
Для ориентированного графа: множество дуг, исходящих из вершины xi записывается  и называются локальной степенью вершины или полустепень исходящей вершины xi.
и называются локальной степенью вершины или полустепень исходящей вершины xi.

Ориентированный граф называется однородным, если все локальные степени имеют одно и тоже значение:
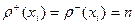 , для любого
, для любого 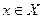
Если  , то вершина x является изолированной.
, то вершина x является изолированной.
Если  , а
, а  , то эта вершина является входом.
, то эта вершина является входом.
Если  ,
,  – вершина является выходом.
– вершина является выходом.
Неориентированный граф является связанным, если любые xi, xj можно соединить цепью, следовательно для ориентированного графа вводятся понятия сильно связанного графа.
Граф сильно связан, если любые xi, xj существуют из xi в xj.
Способы представления графов
1. Матрица смежности

Для неориентированного графа симметрична. Ее вид зависит от выбора алгебраической нумерации вершин. Для ориентированного их можно подобрать так, что матрица будет треугольной.
Свойства матрицы смежности для ориентированного графа:
1) каждый нулевой столбец соответствует источнику
2) каждая нулевая строка – строку
3) если все элементы главной диагонали равны 0, то в графе нет петель
4) появление единицы для любого xi,j . i=j соответствует петле
5) матрица не симметрична
2. Матрица инцидентности
В  неориентированный
неориентированный
в  ориентированный
ориентированный
Ребра должны быть пронумерованы!
3. Матрица изоморфности
В строках через запятую представлены номера входных дуг с плюсом и номера с выходом с минусом.
Пример:

 матрица смежности
матрица смежности
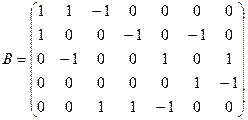 матрица инцидентности
матрица инцидентности
 матрица изоморфности
матрица изоморфности
|
из
5.00
|
Обсуждение в статье: Представление систем с помощью графов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

