 |
Главная |
Лабораторная работа 3.
|
из
5.00
|
Модель парной не линейной регрессии: замена переменных
Задание 3. По имеющимся данным (таблица 2) построить линейную регрессионную модель. Проверить адекватность построенной модели.
Выбрать эмпирическую формулу для описания зависимости между факторами.
Выполнить линеаризацию переменных.
Построить линейную модель относительно вспомогательных переменных.
Найти параметры нелинейной модели.
Проверить адекватность построенной модели.
Таблица 2
| X | Y |
| 0,5 | 0,1 |
| 0,58 | 0,11 |
| 0,66 | 0,12 |
| 0,74 | 0,12 |
| 0,82 | 0,14 |
| 0,9 | 0,13 |
| 0,98 | 0,14 |
| 1,06 | 0,15 |
| 1,14 | 0,16 |
| 1,22 | 0,18 |
| 1,3 | 0,17 |
| 1,38 | 0,18 |
| 1,46 | 0,19 |
| 1,54 | 0,19 |
| 1,62 | 0,19 |
| 1,7 | 0,19 |
| 1,78 | 0,21 |
| 1,86 | 0,2 |
| 1,94 | 0,21 |
1. По имеющимся данным (таблица 2) построить линейную регрессионную модель. Проверить адекватность построенной модели.
Строим линейную регрессионную модель
 ,
,
коэффициенты которой определяем по формулам
 ,
,  ,
,
где
 ,
,  .
.
Подставляя исходные данные, получим
 ,
,
 ,
,
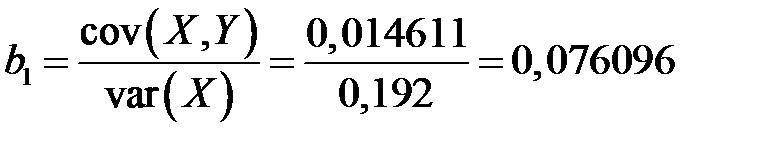 ,
,
 .
.
Таким образом, приходим к уравнению линейной регрессии
 .
.
Находим коэффициент детерминации
 .
.
Наблюдаемое значение  -критерия определяем из равенства
-критерия определяем из равенства
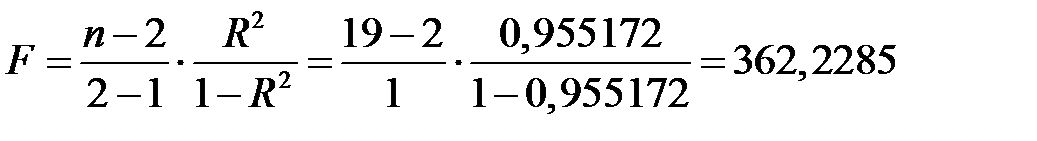 .
.
Критическое значение  -критерия определяем по таблице или с помощью функции EXCEL: FРАСПОБР
-критерия определяем по таблице или с помощью функции EXCEL: FРАСПОБР
 .
.
Так как  , то предложенная линейная модель адекватна.
, то предложенная линейная модель адекватна.
2. Выбрать эмпирическую формулу для описания зависимости между факторами.
Для наиболее часто встречающихся зависимостей парной регрессионной модели, эмпирическую формулу можно выбирать с помощью таблицы 4.1.
Для проверки пригодности выбранной эмпирической формулы, используя исходные данные, находят  и
и  по формулам, приведенным в таблице 4.1. Если
по формулам, приведенным в таблице 4.1. Если  находится среди исходных данных
находится среди исходных данных  ,
,  , то в качестве
, то в качестве  возьмем
возьмем 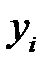 . Если
. Если  не находится среди исходных данных
не находится среди исходных данных  ,
,  , то найдем такой индекс
, то найдем такой индекс  , что
, что  и определим
и определим  с помощью линейной интерполяции
с помощью линейной интерполяции
 . (НЛР_5)
. (НЛР_5)
Далее среди величин  находим самую маленькую. Ей соответствует выбираемая эмпирическая формула.
находим самую маленькую. Ей соответствует выбираемая эмпирическая формула.
Таблица 4.1.
| Номер формулы | 
| 
| Вид эмпирической формулы |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
|
Подставляем исходные данные
| номер формулы | 
| 
| 
| 
|
| 1,22 | 0,155 | 0,18 | 0,025 | |
| 0,984886 | 0,144914 | 0,140611 | 0,00430304 | |
| 1,22 | 0,144914 | 0,18 | 0,03508623 | |
| 0,795082 | 0,155 | 0,13377 | 0,02122951 | |
| 1,22 | 0,135484 | 0,18 | 0,04451613 | |
| 0,795082 | 0,135484 | 0,13377 | 0,00171338 | |
| 0,984886 | 0,155 | 0,140611 | 0,01438928 |
Отсюда получаем эмпирическую формулу
 .
.
3. Выполнить линеаризацию переменных.
Перейдем к обратным величинам. Получим равносильное равенство
 ,
,  .
.
Введем новые переменные
 ,
, 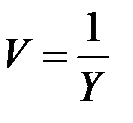 .
.
Тогда модель примет линейный вид
 .
.
Строим данную линейную модель.
4. Построить линейную модель относительно вспомогательных переменных.
 ,
, 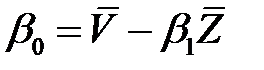 ,
,
где
 ,
, 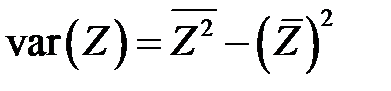 .
.
Подставляя исходные данные, получим
 ,
,
 ,
,
 ,
,
 .
.
5. Найти параметры нелинейной модели.
Таким образом, приходим к уравнению не линейной регрессии
 .
.
Находим коэффициент детерминации
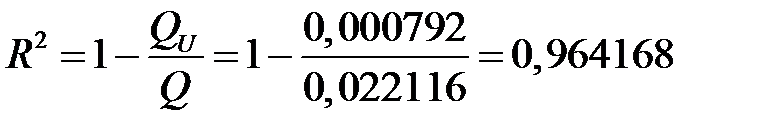 .
.
Наблюдаемое значение  -критерия определяем из равенства
-критерия определяем из равенства
 .
.
Критическое значение  -критерия определяем по таблице или с помощью функции EXCEL: FРАСПОБР
-критерия определяем по таблице или с помощью функции EXCEL: FРАСПОБР
 .
.
Так как  , то предложенная линейная модель адекватна.
, то предложенная линейная модель адекватна.

Вопросы для самопроверки
1. Что называется линеаризацией модели?
2. Что Вы знаете о нелинейной оптимизация на основе исходных переменных?
3. Приведите нелинейные модели по переменным или по параметрам?
4. Сформулируйте алгоритм выбора эмпирической формулы.
|
из
5.00
|
Обсуждение в статье: Лабораторная работа 3. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

