 |
Главная |
Задача о трисекции угла
|
из
5.00
|
Знаменитой была в древности и задача о трисекции угла ( от латинских слов tria – три и section – рассечение , разрезание), т.е.о разделении угла на три равные части с помощью циркуля и линейки. Говорят, что такое ограничение вспомогательных приборов знаменитым греческим философом Платоном.
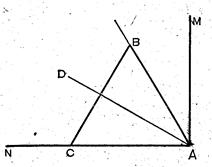 Так, деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60о. Пусть требуется разделить на три равные части прямой угол MAN (Рис. 2). Откладываем на полупрямой
Так, деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60о. Пусть требуется разделить на три равные части прямой угол MAN (Рис. 2). Откладываем на полупрямой 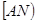 произвольный отрезок
произвольный отрезок 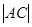 , на котором строим равносторонний треугольник ACB. Так как угол Рис. 2 CAB
, на котором строим равносторонний треугольник ACB. Так как угол Рис. 2 CAB
равен 60о, то 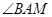 = 30о. Построим биссектрису
= 30о. Построим биссектрису 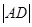
угла САВ, получаем искомое деление прямого угла MAN
на три равных угла: 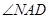 ,
, 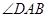 ,
, 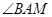 .
.
Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла (например, для углов в 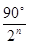 , п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.
, п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.

Рис. 3, а, б, в: конхоида Никомеда
Задача о трисекции угла становится разрешимой и общем случае, если не ограничиваться в геометрических построениях одними только классическими инструментами, циркулем и линейкой. Попытки решения задачи с помощью инструментов и средств были предприняты еще в V в. до н.э. Так, например, Гиппий Элидский, знаменитый софист, живший около 420 г. до н.э., пользовался для трисекции угла квадратрисой. Александрийский математик Никомед ( II в. до н.э.) решил задачу о трисекции угла с помощью одной кривой, названной конхоидой Никомеда (рис. 3), и дал описание прибора для черчения этой кривой.
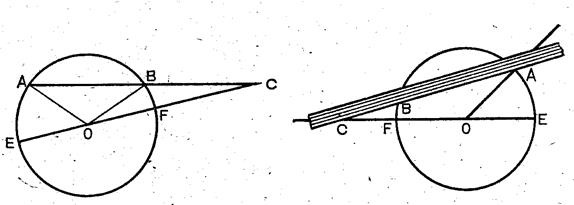
Рис. 4 Рис. 5
Интересное решение задачи о трисекции угла дал Архимед в своей книге «Леммы», в которой доказывается , что если продолжить хорду 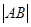 (рис.4) окружности радиуса r на отрезок
(рис.4) окружности радиуса r на отрезок 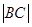 = r и провести через С диаметр
= r и провести через С диаметр 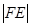 , то дуга BF будет втрое меньше дуги АЕ. Действительно на основе теорем о внешнем угле треугольника и о равенстве углов при основании равнобедренного треугольника имеем:
, то дуга BF будет втрое меньше дуги АЕ. Действительно на основе теорем о внешнем угле треугольника и о равенстве углов при основании равнобедренного треугольника имеем:
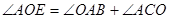 ,
,
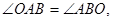
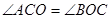 ,
,
значит,
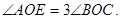
Отсюда следует так называемый способ «вставки» для деления на три равные части угла AOE. Описав окружность с центром O и радиусом 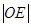 и
и 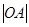 , проводим диаметр
, проводим диаметр 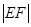 . Линейку CB на которой нанесена длина
. Линейку CB на которой нанесена длина 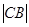 радиуса r (например, помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра
радиуса r (например, помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра 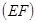 , а сома линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейки с делениями, которая даёт длину определённого отрезка.
, а сома линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейки с делениями, которая даёт длину определённого отрезка.
Вот ещё одно решение задачи о три секции угла при помощи линейки с двумя насечками предложенное Кемпе:
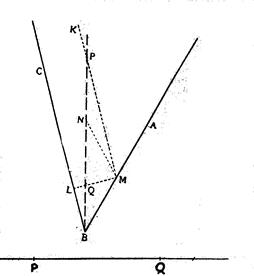 Пусть дан какой – либо угол ABC (Рис. 6); и пусть на лезвии нашей линейки обозначены 2 точки, P и Q (см. ту же фигуру, внизу)
Пусть дан какой – либо угол ABC (Рис. 6); и пусть на лезвии нашей линейки обозначены 2 точки, P и Q (см. ту же фигуру, внизу)
Построение
На одной из сторон угла откладываем от вершины B прямую BA = PQ. Делим ВА пополам в точке М; проводим линии 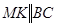 Рис. 6 и
Рис. 6 и 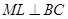 .
.
Возьмём теперь нашу линейку и приспособим её к уже полученной фигуре так, чтобы точка Р
линейки лежала на прямой КМ, точка Q лежала бы
на прямой LM, и в тоже время продолжение PQ линейки проходило бы через вершину данного угла В. тогда прямая ВР и есть искомая, отсекающая третью часть угла В.
Доказательство
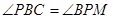 как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM. Точка N есть середина гипотенузы прямоугольного треугольника PQM, а потому PN = N М, а следовательно, треугольник PNM равнобедренный, и значит
как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM. Точка N есть середина гипотенузы прямоугольного треугольника PQM, а потому PN = N М, а следовательно, треугольник PNM равнобедренный, и значит
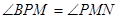
Внешний же 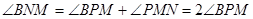
Вместе с тем 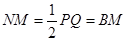 .
.
Значит, 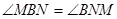
Итак: 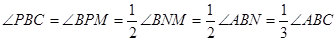
(Ч.Т.Д.).
Приведённое выше решение задачи принадлежит Кемпле, который при этом поднял вопрос, почему Евклид не воспользовался делением линейки и процессом её приспособления для доказательства 4-й теоремы своей первой книги, где вместо этого он накладывает стороны одного треугольника на стороны другого. На это может ответить только, что в задачу Евклида и не входило отыскивание некоторой точки по средствам измерения и процесса приспособления линейки. В своих рассуждениях и доказательствах он просто накладывает фигуру на фигуру – и только.
|
из
5.00
|
Обсуждение в статье: Задача о трисекции угла |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

