 |
Главная |
Ограничения, относящиеся к траекториям сочленений
|
из
5.00
|
| Описание ограничения | Уравнения ограничения | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | Начальное положение схвата Начальная скорость робота Начальное ускорение робота Конечное положение робота при захвате Непрерывность по положению в момент t1 Непрерывность по скорости в момент t1 Непрерывность по ускорению в момент t1 Начальное положение робота при установке Непрерывность по положению в момент t2 Непрерывность по скорости в момент t2 Непрерывность по ускорению в момент t2 Конечное положение робота Конечная скорость робота Конечное ускорение робота | 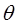 i(t0) = i(t0) = 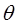 *i0 *i0
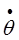 i(t0) = i(t0) = 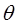 *i0 *i0
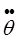 i(t0) = i(t0) = 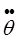 *i0 *i0
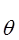 i(t1) = i(t1) = 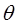 *i1 *i1
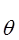 i(t1-) = i(t1-) = 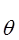 i(t1+) i(t1+)
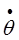 i(t1-) = i(t1-) = 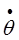 i(t1+) i(t1+)
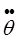 i(t1-) = i(t1-) = 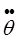 i(t1+) i(t1+)
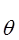 i(t2) = i(t2) = 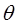 *i2 *i2
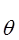 i(t2-) = i(t2-) = 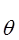 i(t2+) i(t2+)
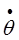 i(t2-) = i(t2-) = 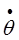 i(t2+) i(t2+)
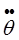 i(t2-) = i(t2-) = 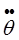 i(t2+) i(t2+)
 i(t3) = i(t3) =  *i3 *i3
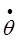 i(t3) = i(t3) = 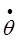 *i3 *i3
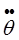 i(t3) = i(t3) = 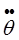 *i3 *i3
|

Рис. 4.8.3. Применение робота в лазерной резке.
Нужно также найти экстремальные значения на траектории перемещения робота с тем, чтобы убедиться, что эти экстремумы не выходят за рабочую поверхность. Таким образом, желательно прибегнуть к полиномам низких степеней путем деления траектории на участки, для которых вычисления выполняются сравнительно легко. Преимуществом таких полиномов низких степеней является то, что для них легче вычислить неизвестные коэффициенты и найти корни их производных при вычислении экстремумов.
Все такие разделенные на участки траектории должны быть непрерывны по положению, скорости и ускорению для достижения плавности движений робота. Для того чтобы это выполнялось, значения перечисленных параметров должны совладать на пересечениях участков.
Приняв во внимание все подобные ограничения, приходим, в конце концов к 14 ограничениям для вычисления неизвестных коэффициентов в точках пересечения трех участков траектории, т. е. траектории типа 4—3—4 и 3—5—3. Три участка начальный, промежуточный и конечный. В табл. 4.8.1 указаны 14 ограничений, относящихся к траекториям, разделенным на участки (рис. 4.8.3).
Чтобы полностью определить три полинома низкой степени при наложении приведенных выше 14 ограничений, сумма показателей степеней переменной t должна быть 14—3, потому что для этих трех различных полиномов имеются три свободных константы. Другими словами, должно быть 14 неизвестных, являющихся коэффициентами полиномов. Три из них являются свободными, так как оyи не умножаются на t. Таким образом, из-за того что полином m-й степени от t должен иметь m+1 коэффициентов, сумма степеней этих полиномов, относящихся к трем участкам, должна быть равна, по меньшей мере 11. Существует множество способов удовлетворить этому условию, в частности 4+3+4, 3+5+3 или 5+2+4. Рассмотрим подробнее некоторые из этих траекторий.
ТРАЕКТОРИЯ ТИПА 4 — 3 — 4
Для трех участков траектории перемещения, а именно: подъем, промежуточный участок и спуск, существуют полиномы четвертой, третьей и четвертой степеней, которые могут до- вольно хорошо аппроксимировать их. Для поиска решения на каждом из участков удобно ввести безразмерную переменную времени τ, такую, что
τ =  и τm = tm - tm-1
и τm = tm - tm-1
где индексы m и m-1 относятся к m-му и (m—1)-му участкам траектории движения робота. Таким образом, при движении по m-му участку траектории безразмерное время τ изменяется от 0 до 1, тогда как реальное время меняется от tm-1 до tm. Введение соотношений (4.8.2) значительно упростит выкладки.
Участок 1: Полином четвертой степени. Пусть ρmi(τ) является полиномиальным представлением m-го участка траектории движения для i-го сочленения. Тогда
ρ1i(τ) = 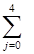 C1j τj = C10 + C11 τ + C12 τ2 + C13 τ3 + C14 τ4, (4.8.3)
C1j τj = C10 + C11 τ + C12 τ2 + C13 τ3 + C14 τ4, (4.8.3)
τ1 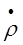 1i(τ) =
1i(τ) = 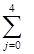 jC1j τj-1 = C11 + 2C12 τ + 3C13 τ2 +4 C14 τ3 , (4.8.4)
jC1j τj-1 = C11 + 2C12 τ + 3C13 τ2 +4 C14 τ3 , (4.8.4)
τ21 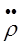 1i(τ) =
1i(τ) = 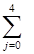 j(j-1)C1j τj-2 = 2C12 + 6C13 τ +12 C14 τ2. (4.8.5)
j(j-1)C1j τj-2 = 2C12 + 6C13 τ +12 C14 τ2. (4.8.5)
Заметим, что эти полиномы должны удовлетворять ограничениям, приведенным в табл. 4.8.1. Таким образом,
ρ1i(0) = 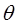 *i0,
*i0, 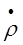 i(0) =
i(0) = 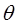 *i0,
*i0, 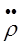 i(0) =
i(0) = 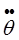 *i0. (4.8.6)
*i0. (4.8.6)
Налагая приведенные ограничения на (4.8.3), (4.8.4) и (4.8.5), получим
ρ1i(τ) = C14 τ4+ C13 τ3 + 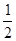
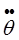 *i0τ21 τ2 +
*i0τ21 τ2 + 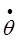 *i0 τ1 τ +
*i0 τ1 τ + 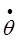 *i0. (4.8.7)
*i0. (4.8.7)
Пример 4.8.1
Определить закон движения схвата при подъеме.
Решение. Искомая зависимость относится к углу 9е и, следовательно, нужно положить i = 6 в (4.8.7). Таким образом,
ρ1i(τ) = C14 τ4+ C13 τ3 + 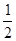
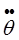 *i0τ21 τ2 +
*i0τ21 τ2 + 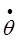 *i0 τ1 τ +
*i0 τ1 τ + 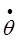 *i0 . (4.8.8)
*i0 . (4.8.8)
Заметим, что в (4.8.7) имеются две неизвестные величины, которые нужно найти, — C14 и C13 ; они определяются из условий непрерывности:
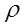 1i(1) =
1i(1) = 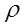 2i(0),
2i(0), 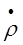 1i(1) =
1i(1) = 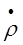 2i(0),
2i(0), 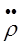 1i(1) =
1i(1) = 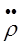 2i(0). (4.8.9)
2i(0). (4.8.9)
Итак, нужно сначала вычислить 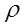 2i(τ).
2i(τ).
Участок 2: Полином третьей степени. Используя подход, примененный для участка 1, получаем
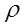 2i(τ) =
2i(τ) =  C2j τj = C20 + C21 τ + C22 τ2 + C23 τ3, (4.8.10)
C2j τj = C20 + C21 τ + C22 τ2 + C23 τ3, (4.8.10)
τ2 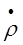 2i(τ) =
2i(τ) = 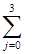 jC2j τj-1 = C21 + 2C22 τ + 3C23 τ2, (4.8.11)
jC2j τj-1 = C21 + 2C22 τ + 3C23 τ2, (4.8.11)
τ22 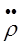 2i(τ) =
2i(τ) =  j(j-1)C2j τj-2 = 2C22 + 6C23 τ. (4.8.12)
j(j-1)C2j τj-2 = 2C22 + 6C23 τ. (4.8.12)
Эти величины должны удовлетворять следующим условиям:
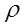 2i(0) =
2i(0) = 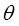 *i1,
*i1, 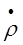 2i(0) =
2i(0) = 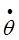 *i1,
*i1, 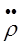 2i(0) =
2i(0) = 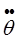 *i1. (4.8. 13)
*i1. (4.8. 13)
Соотношения (4.8.2) и (4.8.9) определяют некоторые из неизвестных коэффициентов. Имеем
C20 = 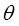 *i0, C21 =
*i0, C21 = 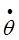 *i1 τ2, C22 =
*i1 τ2, C22 = 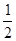
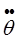 *i1τ22 , (4.8.14)
*i1τ22 , (4.8.14)
C14 + C13 = 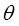 *i1 - (
*i1 - (  *i0 +
*i0 +  *i0 τ1 +
*i0 τ1 + 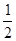
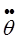 *i0τ21), (4.8.15)
*i0τ21), (4.8.15)
4τ1-1C14 + 3τ-1C13 + τ2-1C21 = - ( 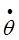 *i0 + τ 1
*i0 + τ 1 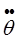 *i0), (4.8.16)
*i0), (4.8.16)
6τ1-2C13 + 12τ-2C14 - 2τ2-2C22 = - 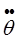 *i0. (4.8.17)
*i0. (4.8.17)
В конце второго участка мы, однако, должны обеспечить выполнение условий непрерывности, т. е.
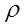 2i(1) =
2i(1) = 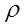 3i(0),
3i(0), 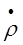 1i(1) =
1i(1) = 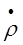 3i(0),
3i(0), 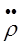 2i(1) =
2i(1) = 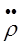 3i(0). (4.8.18)
3i(0). (4.8.18)
Таким образом, чтобы вычислить дополнительные коэффициенты, нужно найти полином для третьего участка.
Участок 3: Полином четвертой степени. По аналогии с подходами, использованными для участков 1 и 2, имеем
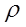 3i(τ) =
3i(τ) = 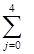 C3j τj = C30 + C31 τ + C32 τ2 + C33 τ3 + C34 τ4, (4.8.10)
C3j τj = C30 + C31 τ + C32 τ2 + C33 τ3 + C34 τ4, (4.8.10)
τ3 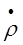 3i(τ) =
3i(τ) = 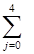 jC3j τj-1 = C31 + 2C32 τ + 3C33 τ2 + 4C34 τ3, (4.8.11)
jC3j τj-1 = C31 + 2C32 τ + 3C33 τ2 + 4C34 τ3, (4.8.11)
τ23 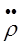 3i(τ) =
3i(τ) = 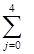 j(j-1)C3j τj-2 = 2C32 + 6C33 τ + 12C34τ2. (4.8.12)
j(j-1)C3j τj-2 = 2C32 + 6C33 τ + 12C34τ2. (4.8.12)
Начальные условия имеют вид
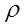 3i(0) =
3i(0) = 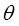 *i2,
*i2, 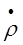 3i(0) =
3i(0) = 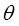 *i2,
*i2, 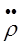 3i(0) =
3i(0) = 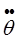 *i2, (4.8.22)
*i2, (4.8.22)
которые в сочетании с формулами (4.8.8) - (4.8.10) дают
C30 = 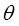 *i1, C31 =
*i1, C31 = 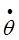 *i1 τ3, C32 =
*i1 τ3, C32 = 
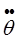 *i1 τ23.
*i1 τ23.
Соотношения непрерывности (4. 8.18) дают теперь
C20 + C21 + C22 = 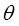 *i2 -
*i2 - 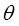 *i1, (4.8.24)
*i1, (4.8.24)
τ2-1C21 + 2τ2-1C22 + 3τ2-1C23 - τ3-1C31 = 0, (4.8.25) 2τ2-2C22 + 6τ2-2C23 - 2τ3-2C32 = 0, (4.8.26)
Наконец, на конце участка должны выполняться ограничения:
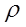 3i(1) =
3i(1) = 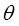 *if,
*if, 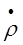 3i(1) =
3i(1) = 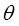 *if,
*if, 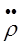 3i(1) =
3i(1) =  *if, (4.8.27)
*if, (4.8.27)
Используя соотношения (4.8.27) и (4. 8.19) — (4.8.21), получаем
C31 + C32 + C33 + C34 = 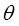 *if -
*if - 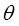 *i2, (4.8.28)
*i2, (4.8.28)
C31 + 2C32 + 2C33 + 4C34 =  *ifτ3, (4.8.29) 2C32 + 6C33 + 12C34 =
*ifτ3, (4.8.29) 2C32 + 6C33 + 12C34 =  *ifτ23, (4.8.31)
*ifτ23, (4.8.31)
Отметим, что, так как в общем случае  *i1 ,
*i1 ,  *i1 ,
*i1 ,  *i2 и
*i2 и  *i2 неизвестны, мы определили в явном виде только пять из 14 неизвестных коэффициентов, которыми являются C10, C11, C12, C13, C14, C20, C21, C22, C23, C30, C31, C33 и C34. Известные коэффициенты – это
*i2 неизвестны, мы определили в явном виде только пять из 14 неизвестных коэффициентов, которыми являются C10, C11, C12, C13, C14, C20, C21, C22, C23, C30, C31, C33 и C34. Известные коэффициенты – это
(C10, C11, C12, C20, C30) ≡ ( 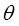 *i0,
*i0,  *i0 τ1,
*i0 τ1, 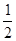
 *i0τ21,
*i0τ21, 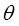 *i1,
*i1, 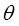 *i2).(4.8.31)
*i2).(4.8.31)
Остальные девять уравнений (4.8.15) - (4.8,17), (4.8.24) - (4.8.26) и (4.8.28) — (4.8.30) могут быть представлены в матричной форме, а именно
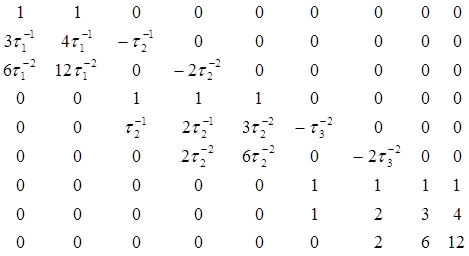 Х
Х  =
=
= 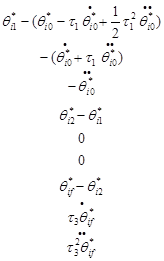 (4.8.32)
(4.8.32)
Представляя для простоты уравнение (4.8.32) в компактной форме, получаем
ВС = δ, (4.8.33)
где В — 9Х9-матрица коэффициентов С, а δ — некоторый век- торный массив, относящийся к изменениям углов в сочленениях и их производных по времени, как показано в (4.8.32). Полное решение для С (остальные девять коэффициентов, которые нужно найти) имеет вид
С = В-1 δ (4.8.33)
Пример 4.8.2
Найти полные решения в явной форме для трех полиномов 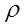 1(τ),
1(τ), 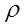 2(τ) и
2(τ) и 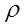 3(τ)
3(τ)
Решение. Можно показать, что выражения для коэффициентов C13, C14, C21, C22, C23, C31, C33 и C34 имеют вид (см. положение А)
C13 = (τ2-1τ3 + 2τ1-1 τ3 + 2 + 3τ1-1 τ2)-1 × {2 δ1*(4 + 2 τ2-1τ3 + 2τ1-1 τ3 + 3τ1-1 τ2) – δ2* τ2-1 τ1(3 + τ2-1τ3) + 2δ1
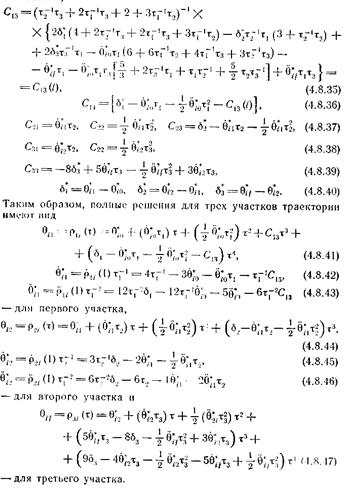
ТРАЕКТОРИЯ ТИПА 3 — 5 — 3
Используя ту же процедуру, что и при выводе соотношений (4.8.41) — (4.8.47), легко показать, что для трех участков траектории можно получить следующие выражения, описывающие движение сочленений:
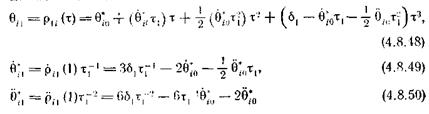
- для первого участка,
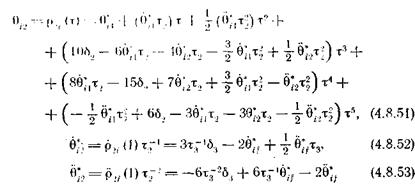 -
-
для второго участка и
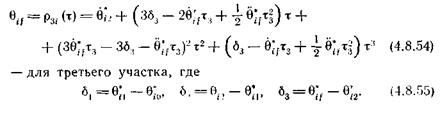
|
из
5.00
|
Обсуждение в статье: Ограничения, относящиеся к траекториям сочленений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

