 |
Главная |
Точечный заряд и проводящая сфера
|
из
5.00
|
Пусть мы имеем проводящую сферу радиуса R и точечный заряд +q, расположенный на расстоянии d от центра сферы (рис. 5).

Рис. 5
Определим силу, действующую на заряд со стороны сферы. Сначала заземлим сферу. Чтобы решать задачу методом изображений, нужно найти такое расположение точечных зарядов, при котором одной из эквипотенциальных поверхностей является сфера. Задача с двумя неравными точечными зарядами как раз и дает именно такую картину эквипотенциальных поверхностей. Один из этих зарядов +q расположен там, где указано в условии задачи. Но какова должна быть величина второго заряда (заряда-изображения), и где он должен быть расположен?
Предположим, что заряд q расположен на прямой, соединяющей центр сферы и заряд q в точке, расположенной на расстоянии х от центра сферы (рис. 6).
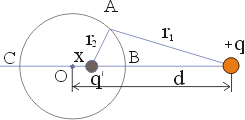
Рис. 6
Может ли эта сфера быть эквипотенциальной поверхностью, каковы должны быть х и q, чтобы она ей была? Пусть потенциал сферы равен нулю. Рассмотрим произвольную точку А сферы, ее потенциал равен нулю. Он создается зарядом q, расположенным от нее на расстоянии r1, и зарядом q, расположенном на расстоянии r2. Следовательно, A = или = kqr1+kqr2. То есть -qq = r1r2. Для точки B сферы мы можем записать
| k | q R-x | +k | q d-R | = 0 или - | q q | = | d-R R-x | . |
Для точки C имеем
| k | q R+x | +k | q d+R | = 0 или - | q q | = | d+R R+x | . |
Таким образом имеем уравнение для определения х
| d-R R-x | = | d+R R+x | . |
Отсюда x = R2/d.
Если мы поместим точечный заряд q на расстоянии х от центра сферы, то сфера будет эквипотенциальной поверхностью. Величина заряда q легко определится из соотношения
| q = - | R-x d-R | q = - | R d | q. |
Таким образом, имеем систему двух точечных зарядов, расположенных так, как на рис. 7.

Рис. 7
На заряд +q со стороны сферы (или заряда-изображения q) действует сила притяжения
| F = k | q|q| (d-x)2 | = k | q2 d2-R2 | . |
Mы рассмотрели случай заземленной проводящей сферы. А как быть в том случае, если сфера имеет заряд Q или несет ненулевой потенциал? Ответ на этот вопрос очень прост - в центр сферы нужно добавить еще один точечный заряд q, величину которого определим из условия эквипотенциальности сферы.
Рассмотрим незаряженную металлическую изолированную сферу и заряд +q, расположенный на расстоянии d от ее центра. Какая сила действует на заряд? Cфера останется незаряженной. Произойдет лишь перераспределение зарядов по поверхности сферы, связанное с взаимодействием с зарядом +q. Ближняя к заряду часть сферы приобретет отрицательный заряд, а дальняя - положительный, так как электроны притянутся к заряду (рис. 8).

Рис. 8
Чтобы решить задачу, кроме заряда q, расположенного от центра сферы на расстоянии R2d , в центре сферы надо расположить еще один заряд q (рис. 9).

Рис. 9
Появление в центре сферы заряда q не меняет ее эквипотенциальности. Потенциал любой точки сферы создается теперь уже тремя зарядами - q, q и q. Суммарный потенциал, создаваемый зарядами q и q на поверхности сферы равен нулю, следовательно потенциал любой точки сферы определяется только зарядом q. Он равен = kqR . Если сфера изолирована, то заряд q определится из условия
| q+q = , q = | R d | q = -q. |
Поля и потенциалы вне сферы определяются по принципу суперпозиции как результат наложения полей всех трех зарядов. Сила, действующая на заряд +q определится следующим образом
| F = k | q|q|
| - k | qq d2 | . |
Если теперь вместо изолированной сферы и заряда q мы будем рассматривать тот же заряд и сферу, имеющую либо заряд Q, либо потенциал , то, используя метод изображений, получим систему точечных зарядов: заряд q, расположенный на расстоянии d от центра сферы, заряд-изображение q, расположенный на расстоянии R2d от центра сферы, и заряд-изображение q, расположенный в центре сферы. Величина q определится из условия, что потенциал сферы должен быть равен
| = k | q R | . |
Если мы знаем заряд сферы Q, то q = Q. Если же нам известен ее потенциал , то q = Rk.
Точечный заряд вблизи границы раздела двух диэлектриков
Пусть точечный заряд +q находится на расстоянии а от плоской границы двух бесконечно протяженных однородных диэлектриков с проницаемостями 1 и 2 (рис. 10).

Рис. 10
Определим силу, действующую на заряд, и потенциал электрического поля методом изображений.
Допустим, что заряд-изображение имеет величину q и расположен на расстоянии a снизу от поверхности МN, разделяющей диэлектрики (рис. 11), так как именно там будет находиться изображение светящейся точки q в плоском зеркале MN.

Рис. 11
Величину заряда-изображения можно найти из граничных условий для нормальной (перпендикулярной границе) и тангенциальной (параллельной границе) составляющих вектора напряженности электростатического поля. На границе раздела двух диэлектрических сред нормальная составляющая поля подчиняется условию 1En1 = 2En2 , где En1 и En2 - нормальные составляющие поля в диэлектриках с проницаемостями 1 и 2, соответственно. Тангенциальная составляющая поля при переходе из среды с диэлектрического проницаемостью 1 в среду с диэлектрической проницаемостью 2 остается неизменной, то есть E1 = E2. Подробнее о граничных условиях на границе раздела двух сред поговорим в конце задачи.
Найдем нормальную и тангенциальную составляющие вектора напряженности электрического поля в точке А, расположенной на границе раздела диэлектриков,
En1 = E1 cos 1, En2 = E2 cos 2,
E1 = E1 sin 1, E2 = E2 sin 2,
где 1 и 2 - углы, которые составляют вектора напряженности в первой и во второй средах соответственно. Отсюда легко получить соотношение tg 1tg 2 = 12, которое потребуется нам в дальнейшем.
Если бы не было среды с проницаемостью 2, то в точке A напряженность поля была бы равна E1 и ее создавал бы один заряд +q. Но поскольку вторая среда присутствует, то напряженность поля равна вектору E2 и составляет с перпендикуляром угол 2. Если дело происходит в вакууме, то это возможно в случае, когда в точке B находится заряд q, создающий в точке A поле, напряженность которого обозначим E. Ясно, что E удовлетворяет равенству
| E1 | + | E | = | E2 | . |
Анализ граничных условий приводит к выводу: если 1 > 2, то 1 > 2, и в точке B должен находиться отрицательный заряд (рис. 12);

Рис. 12
если же 1 < 2, то 1 < 2 и в точку B должен быть помещен положительный заряд (рис. 13).

Рис. 13
Разберем случай 1 > 2. Спроецировав левую и правую части уравнения
| E1 | + | E | = | E2 |
на горизонтальное и вертикальное направления, получим
E1 sin 1-E sin 1 = E2 sin 2 и E1 cos 1-E cos 1 = E2 cos 2.
Используя граничные условия и поделив первое уравнение на второе, имеем
| E1-E E1+E | = | tg2 tg1 | = | 2 1 | . |
Модуль вектора напряженности поля, которое создает в точке A заряд +q определяется его величиной и расстоянием r до точки A: E1 = kq/r. Заряд q в точке A создает поле, модуль вектора напряженности которого E = k|q|r. Тогда для определения величины заряда q имеем уравнение
| q-|q| q+|q| | = | 2 1 | . |
Отсюда определяем модуль заряда q
| |q| = q | 1-2 1+2 | . |
Сила взаимодействия зарядов определяется по закону Кулона
| F = k | q|q| (2a)2 | = k | q2 4a2 | 1-2 1+2 | . |
Потенциал произвольной точки C, расстояние от которой до точки, в которой находится заряд +q, равно r1, а до точки В, в которой находится заряд q, равно r2, легко определить по принципу суперпозиции полей. Если точка С находится в среде с проницаемостью 1, то по ее потенциал q определяется равенством
| = | q 1r1 | + | (1-2)·q 1(1+2)·r2 | ; |
если же точка C находится в диэлектрике с проницаемостью 2, то
| = | r·q (1+2)·r1 | . |
Случай, когда в точке B находится положительный заряд-изображение q, рассчитывается аналогично; для величины q получим выражение
| q = | 2-1 1+2 | q r1 | . |
Если диэлектрическая проницаемость первой среды больше, чем второй, то заряд отталкивается от границы диэлектриков, при обратном соотношении - притягивается. Заряд, находившийся вначале в среде с большей проницаемостью, отталкиваясь от границы, стремится уйти в бесконечность. Заряд, вначале находившийся в среде с меньшей проницаемостью, притягивается к границе, пересекает ее, а затем, находясь уже в другой среде отталкивается от границы, стремясь уйти в бесконечность. Естественно, все сказанное справедливо только в том случае, если можно пренебречь силой трения, действующей на заряд со стороны среды.
И в заключение этой задачи поговорим о граничных условиях на границе раздела двух сред. Начнем с рассмотрения диэлектрических сред. Пусть мы имеем плоскую границу двух однородных диэлектриков с различными проницаемостями 1 и 2. Обозначим через
| E1 | и | E2 |
напряженности электрического поля в первой и во второй средах соответственно. Разложим векторы
| E1 | и | E2 |
на две составляющие - нормальную En1 и En2 и тангенциальную E1 и E2.

Рис. 14
Выясним теперь, как связаны тангенциальные составляющие поля при переходе из одной среды в другую. Выберем любые две пары точек, расположенных очень близко к друг к другу и разделенных поверхностью (рис. 14). Пара точек A1 и B1 находится в первом диэлектрике, а пара точек A2 и B2 находится во втором диэлектрике. Если тангенциальные составляющие полей в разных диэлектриках будут различными, то работы поля при перемещении какого-либо заряда вдоль линий A1B1 и A2B2 будут различными. Будем приближать точки A1 и A2, B1 и B2 друг к другу, в конце концов мы получим две бесконечно близких линии A1B1 и A2B2. Поскольку электрическое поле потенциально, то работа по перемещению заряда между какими-либо точками не зависит от траектории. У нас же получается, что работа поля по перенесению заряда по двум бесконечно близким отрезкам A1B1 и A2B2 различна. Следовательно наше допущение о неравенстве тангенциальных составляющих поля не верно, так как ведет к нарушению потенциальности поля.
Таким образом, на границе раздела двух диэлектриков тангенциальные составляющие поля в разных средах одинаковы или непрерывны, то есть E1 = E2.

Рис. 15
Получим граничные условия для нормальных составляющих поля. Для этого выделим на поверхности прямоугольник S столь малый, что поля в диэлектриках с проницаемостями 1 и 2 на его площади не меняются. Построим на нем параллелепипед высоты 2L (рис. 15). Величина L должна быть достаточно малой, чтобы электрическое поле на протяжении отрезка L оставалось постоянным. Определим поток поля через поверхность прямоугольного параллелепипеда. Потоки через боковые грани поверхности равны нулю, так как для них углы между напряженностью поля и нормалями (перпендикулярами) к поверхности равны 9. Таким образом остается только посчитать потоки через верхнюю и нижнюю грани параллелепипеда. Поскольку верхняя грань находится в среде с проницаемостью 1, а нижняя - в среде с проницаемостью 2, суммарный поток через них определится следующим образом
= ниж+верх = 1 En1S-2 En2S.
С другой стороны, по теореме Гаусса имеем = , так как свободных зарядов внутри параллелепипеда нет. Следовательно, 1 En1 = 2 En2.
Если мы имеем две металлические среды, то тангенциальная составляющая поля на поверхности равна нулю (если бы она не была равна нулю, то электроны бы двигались против поля, а это означает, что точки на поверхности металла имеют разные потенциалы).
Точечный заряд и проводящие плоскости, образующие двугранный угол
Двугранный угол между двумя заземленными металлическими плоскостями равен . Внутри угла на расстоянии a и b от плоскостей находится точечный заряд +q. Найти электрическое поле внутри угла. Рассмотреть случаи: а) = 9, б) = 6, в) = 45.
Рассмотрим случай = 9. В оптике есть аналогичная задача - построение изображения точечного источника в системе плоских зеркал, образующих двугранный угол = 9. Начнем с ее рассмотрения. Источник обозначим буквой S, плоскости зеркал OA и OB. Построим изображение источника S в зеркале OA, получим мнимый источник S1, расположенный на расстоянии a снизу от плоскости зеркала OA (рис. 16а), для его построения нам нужно найти точку, симметричную S относительно плоскости OA.


Рис. 16а Рис. 16б
Строя изображение точки S в зеркале OB, получим мнимый источник S2. Еще надо построить изображение S1 в зеркале OB и изображение S2 в зеркале OA. Эти изображения совпадут и будут находиться в точке S3 (мнимый источник). Для построения точки S3 плоскости зеркал нужно продолжить влево и вниз и найти точки, симметричные точкам S1 и S2 относительно этих плоскостей. В нашей задаче имеем три заряда-изображения, расположенные в точках S1, S2 и S3. В точках S1 и S2 расположены заряды -q, в точке S3 - заряд +q (рис. 17).

Рис. 17
Заряд и его изображения одинаковы по величине, но противоположны по знакам.
Тогда поле внутри двугранного угла определится по принципу суперпозиции как векторная сумма полей каждого из зарядов. Ее расчет достаточно стандартен и поэтому здесь мы его приводить не будем.


Рис. 18 Рис. 19
Если угол = 6, то имеем 5 зарядов-изображений, расположенных так, как показано на рис. 18. В случае = 45 имеем семь зарядов-изображений (рис. 19). В геометрической оптике при решении задачи построения изображения точечного источника в ситеме плоских зеркал, угол между которыми равен = 2m, показывается, что число изображений равно m-1. Воспользовавшись этим результатом, мы легко можем решить задачу для точечного заряда и проводящих плоских поверхностях, образующих угол .
P.S. Каждый раз, решая задачу методом изображений, мы подбирали системы точечных зарядов, которые создают точно такие же поля, как и заряды, индуцированные на поверхности проводника. Положение и величины зарядов выбираются таким образом, чтобы одна из эквипотенциальных поверхностей поля, создаваемого заданными зарядами и зарядами-изображениями, совпадала бы с поверхностью проводника. С помощью этих зарядов находится только поле вне проводника, внутри проводника поля нет. Но, несмотря на свою привлекательность, метод изображений далеко не универсален. Достаточно поместить точечный заряд снаружи двугранного угла, образованного проводящими плоскостями, чтобы задачу уже невозможно было решить этим методом (рис. 16б). Хотя система точечных зарядов, изображенная на рис 17, и обеспечивает эквипотенциальность поверхности двугранного угла, но она не дает решения задачи. Дело в том, что фиктивные заряды-изображения можно помещать только по другую от реального заряда сторону проводящей поверхности. В той точке пространства, где находится точечный заряд, напряженность поля обращается в бесконечность. Поэтому, если мы поместим фиктивный заряд по одну сторону с реальным, то в точке его нахождения напряженность поля обратится в бесконечность, чего на самом деле нет.
Список литературы
Р. Фейман, Р. Лейтон, М. Сэндс, Феймановские лекции по физике, т. 5. - М., Мир, 1977, 300 с.
В. В. Батыгин, И. Н. Топтыгин, Сборник задач по электродинамике - М., Наука, 1970, 504 с.
И. Е. Тамм, Основы теории электричества - М., Наука, 1989, 504 с.
Е. И. Бутиков, А. А. Быков, А. С. Кондратьев, Физика для поступающих в ВУЗы. Учебное пособие - М.,Наука, 1982, 608 с.
Физическая энциклопедия / Под ред. А. М. Прохорова. - М., Большая Российская энциклопедия. Т. 3. 1992, 672 с.
|
из
5.00
|
Обсуждение в статье: Точечный заряд и проводящая сфера |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

