Ограниченный метод Хартри-Фока . Уравнения Рутана .

Лекции 9-10.

АКТУАЛЬНЫЕ ЗАДАЧИ И СТРУКТУРА СОВРЕМЕННОЙ КВАНТОВОЙ ХИМИИ.

План.

I. Обзор современных квантово-химических методов

1. Квантово-химическая модель

2. Метод Хартри-Фока

2.1. Основные приближения

2.2. Вариационный принцип

2.3. Правила Слейтера

2.4. Уравнения Хартри-Фока

2.5. Ограниченный метод Хартри-Фока. Уравнения Рутана.

2.6. Неограниченный метод Хартри-Фока

2.8. Метод ОХФО

3. Методы конфигурационного взаимодействия

3.1. Разложение волновой функции в конфигурационный ряд

3.2. Метод конфигурационного взаимодействия

3.3. Классификация корреляционной энергии на основе метода КВ

3.4. Метод МКССП

3.5. Метод обобщенных валентных связей (GVB)

4. Методы, основанные на теории возмущений

5. Метод связанных кластеров и родственные методы

6. Теория функционала плотности

7. Полуэмпирические методы

II. Развитие методов квантовой химии

 

I . Обзор современных квантово - химических методов

Квантово - химическая модель

Математической моделью называется упрощенное математическое описание системы, в котором исключены незначительные и сложные детали и учитываются только главные свойства моделируемого объекта. Одной из наиболее распространенных моделей изолированной молекулы является нерелятивистское стационарное многоэлектронное уравнение Шредингера в приближении Борна-Оппенгеймера:

ĤΨ(r) = EΨ(r)

Здесь Ψ(r) - волновая функция, зависящая явно от координат всех электронов r и не зависящая от координат ядер; Ĥ - нерелятивистский гамильтониан молекулы.

Эта модель не учитывает релятивистского увеличения массы электронов, влияния электронов на движение ядер и влияние внешней среды на поведение отдельной молекулы. В то же время она учитывает наиболее значимые молекулярные энергетические эффекты - взаимодействие электронов с ядрами молекулы и взаимное отталкивание электронов. Эта модель может быть упрощена или усложнена. Например, можно считать, что электроны двигаются независимо друг от друга - т.е. многоэлектронная волновая функция является произведением одноэлектронных функций (приближение Хартри), что сильно упростит вычисления, но сделает результат значительно более грубыми.

Особенностью моделей, используемых при моделировании молекулярных систем, является невозможность их точного аналитического решения. В отличие от многих простых математических моделей, модели молекулярных систем могут быть решены точно только для тривиальных систем, (например, атома H, молекулярного иона водорода H₂⁺). Для всех практически значимых химических систем решение соответствующих электронных уравнений возможно только приближенно.

Квантово - химической моделью называется способ получения электронной энергии молекулы и ее волновой функции (матрицы плотности), не зависящий от размера системы и молекулярной структуры и определяемый:

1. Математической моделью явления.

2. Теоретической процедурой решения уравнений, соответствующих модели.

3. Базисом атомных орбиталей.

Квантово-химическая модель обязана подчиняться следующим принципам:

1. Уникальность решения . Она дает уникальное (хотя и приближенное) решение уравнения Шредингера для заданной конфигурации ядер, электронного и спинового состояния молекулы.

2. Трансферабельность. Она применима к химической системе произвольного размера и с произвольной молекулярной структурой (хотя согласие результатов расчета с экспериментом и практическая осуществимость такого расчета может зависеть от конкретных параметров системы).

3. Точность. В идеале модель должна давать высокоточные количественные результаты, совпадающие с экспериментом в пределах экспериментальной погрешности. Как минимум, модель должна предсказывать качественные закономерности для групп молекулярных систем.

4. Вычислительная эффективность . Расчеты в рамках данной модели должны быть осуществимы с использованием современных компьютерных технологий. Не каждая квантово-химическая модель удовлетворяет всем перечисленным принципам. Характеристики конкретных современных квантово-химических моделей будут рассмотрены далее.

5. Воспроизведение точных результатов соответствующей N-электронной задачи. Квантово-химический метод, явно учитывающий взаимодействие n-электронов должен давать такое решение, которое совпадает с точным решением уравнения Шредингера для n-электронной задачи, допускающей точное (аналитическое) решение.

Метод Хартри-Фока

Основные приближения

Рассмотрим изолированную молекулу, не испытывающую внешних воздействий. Для ее описания используем следующую модель:

1. Учитывается только притяжения электронов к ядрам и отталкиванием электронов друг от друга;

2. Состояние молекулы стационарно (ее энергия E не зависит от времени);

3. Ядра атомов неподвижны и их координаты R точно определены (адиабатическим приближением).

С учетом сделанных предположений, волновая функция молекулы Ψ зависит только от координат электронов и подчиняется стационарному уравнению Шредингера:

ĤΨ(r) = EΨ(r)

Поскольку мы пренебрегли всеми взаимодействиями, за исключением взаимодействием электронов с ядрами и электронов друг с другом, гамильтониан молекулы Ĥ включает только три члена: кинетическую энергию электронов, притяжение электронов к ядрам атомов и отталкивание электронов между собой. Тогда гамильтониан молекулы есть сумма двух членов

Ĥ= ĥ +Ĝ (2.2)

Однако поведение системы электронов зависит от того, в каком спиновом состоянии находится каждый из них. Пусть отдельный (например, изолированный) электрон i описывается волновой функцией φ:

φ = φ(r_i,σ_i)

Здесь r_i - пространственные (например, декартовы) координаты электрона i, σ_i - его спиновая переменная. Т.к. проекция спина электрона s_z может принимать только два значения (+ħ/2 и –ħ/2), то спиновая переменная также принимает только два значения (назовем их, соответственно, α и β).

Сделаем еще одно предположение, которое, строго говоря, является приближением: допустим, что спин и пространственные переменные независимы и волновую функцию отдельного электрона можно представить в виде произведения двух независимых функций:

φ(r,σ) = φ(r)η_ς(σ) (2.7)

Здесь η_ς(σ) - спиновая волновая функция электрона со спином ς , т.е. волновая функция, определяющая вероятность обнаружить данный электрон со спином σ=ς. Мы не знаем явный вид этой функции, но очевидно, что она может принимать только строго определенные значения.

φ(r_i)η_iα(σ) → φ(i)α(i) (2.8)

φ(r_i)η_iβ(σ) → φ(i)β(i) (2.9)

Смысл записи (2.8) состоит в том, что пространственная вероятность обнаружения электрона i описывается квадратом модуля функции φ_i(r), а его проекция спина в этом состоянии +1/2ħ (т.е. α). Одноэлектронные волновые функции вида (2.7), являющиеся решением молекулярного уравнения Шредингера, называются спин - орбиталями, а их пространственные компоненты φ(r) - одноэлектронными орбиталями молекулы.

С учетом сделанных обозначений стационарное уравнение Шредингера (2.1) следует записать в виде:

ĤΨ(q₁, q₂, … q_N) = EΨ(q₁, q₂, … q_N) (2.10)

где q_i=(r_i,σ_i) - совокупность пространственных и спиновых переменных электрона i. Вид оператора Ĥ при этом совершенно не изменяется, и он по-прежнему действует только на пространственные координаты электронов. Спиновая часть волновой функции является для операторов ĥ и Ĝ просто постоянным множителем, который можно вынести за скобки. Эта часть, однако, будет иметь значение при проведении интегрирования по всем координатам электронов, включая спиновые переменные.

Наша задача состоит в нахождении волновой функции Ψ(q₁, q₂, … q_N) из уравнения (2.10), в котором гамильтониан Ĥ задан формулами (2.2)-(2.5). Это уравнение является 3N-мерным дифференциальным уравнением второго порядка в частных производных, решение которого требует дальнейших упрощений.

Важное приближение, позволяющее значительно упростить уравнение (2.10) было предложено английским физиком Д. Хартри. Многоэлектронная волновая функция Ψ(q₁, q₂, … q_N) представляет собой произведение функций, зависящих от координат только одного электрона:

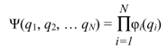
Оно соответствует системе, в которой все электроны движутся независимо друг от друга, что в случае молекулы, конечно же, неверно. Приближение Хартри также не подчиняется принципу Паули, который гласит, что волновая функция, описывающая состояния электронов, должна менять знак при перестановке координат любых двух электронов. Выход из этой ситуации был предложен советским физиком В.А. Фоком и одновременно американским физиком Дж. Слейтером: необходимо подействовать на функцию специальным оператором (т.н. оператором антисимметризации A), который превращает любое произведение функций в антисимметричную относительно перестановки двух электронов.

В соответствие с физическим смыслом волновой функции на функцию (2.15) должно быть наложено еще одно физическое условие - условие нормировки:

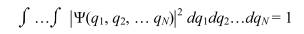
которое означает, что вероятность обнаружить любой из N электронов молекулы во всем пространстве с любым спином равна 1.

Вариационный принцип

Энергия, соответствующая любой нормированной электронной волновой функции Ψ, которая может быть, а может и не быть точным решением уравнения Шредингера, всегда больше или равна энергии E₀, соответствующей точной нормированной волновой функции основного состояния Ψ₀:

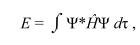
Вариационный принцип имеет два очень важных следствия:

Во-первых, мы можем использовать его для нахождения точной волновой функции: варьируя пробную функцию Ψ так, чтобы добиться минимума энергии функционала (2.20), мы приближаемся к точной волновой функции.

Во-вторых, на основе вариационного принципа мы можем сравнивать качество различных приближений: если две функции получены путем вариации функционала (2.20), то более точным решением уравнения (2.1) будет та, которая дает меньшую энергию.

Правила Слейтера

Для того, чтобы развивать дальнейшую теорию, необходимо разработать приемы работы с детерминантными волновыми функциями. Существует несколько простых правил, значительно упрощающих вычисления с такими функциями. Они касаются действия единичного оператора и операторов ĥ и Ĝ на произвольные функции вида (2.18) и называются правилами Слейтера.

Уравнения Хартри-Фока

Используя вариационный принцип и правила Слейтера, можно вывести уравнения для нахождения волновых функций (2.18), удовлетворяющих стационарному электронному нерелятивистскому уравнению Шредингера (2.10). При их выводе используется математический аппарат курса вариационного исчисления.

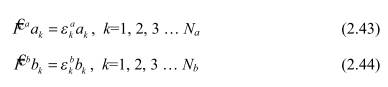
Уравнения (2.43), (2.44) называются уравнениями Хартри-Фока.

Ограниченный метод Хартри-Фока . Уравнения Рутана .

До сих пор развиваемая теория оставалась общей в том смысле, что не зависела от типа рассматриваемых молекул. Если считать, что в молекуле четное число электронов и число электронов со спином α равно числу электронов со спином β, т.е. N_α/2 = N_β/2 = n . Кроме того, предположим, что все электроны спарены, т.е. пары электронов занимают одну и ту же пространственную орбиталь, различаясь только спином. Качество этого приближения ухудшается при растяжении связей и, наконец, нарушается при диссоциации связи, когда электронам энергетически выгоднее находиться в неспаренном состоянии. Такой тип молекул в действительности очень распространен и называется молекулами с замкнутыми ( закрытыми ) электронными оболочками. Тогда уравнения Хартри-Фока сводятся к более простому виду:

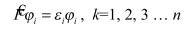
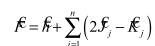
Уравнение Хартри-Фока, в принципе, позволяет найти волновые функции многоэлектронной системы, однако в случае молекул его прямое решение все еще оказывается весьма сложным. Для описания молекулярных систем требуется сделать дополнительные упрощения. Будем искать одноэлектронные функции многоэлектронной системы в виде линейной комбинации одноэлектронных функций центрированных на ядрах атомов (атомных орбиталей). Это приближение называется приближением "Молекулярная Орбиталь – Линейная Комбинация Атомных Орбиталей", или МО - ЛКАО.

Тогда можно показать, что выражение (2.46) можно представить в виде системы линейных уравнений (уравнения Рутана):

или в матричном виде:

FC=SC ε , (2.51)

Здесь матрица F - т.н. оператор Фока (фокиан ). Матрица P называется матрицей плотности, S – называются интегралами перекрывания, χ _i - базисные функции, центрированные на ядрах атомов, r - векторы пространственных координат электронов. Величины ε_i называются одноэлектронными энергиями или энергией молекулярной орбитали i. Можно показать, что энергия МО с точностью до знака равна энергии удаления электрона с данной МО (т.е. потенциалу ионизации с данной МО) при условии, что орбитали системы в ходе этого процесса рассматриваются как неизменные (Теорема Кумпанса).

IP _i = -ε _i (2.56)

Решение уравнения Рутана (2.51) генерирует набор коэффициентов c_ij, которые являются коэффициентами разложения молекулярной орбитали φ _i (r _i)по базисным функциям (атомным орбиталям) χ (r _i).

Однако, уравнения Рутана имеют еще одну сложность - фокиан зависит от матрицы плотности, которая, в свою очередь определяется через c_ij - т.е. через решения самих уравнений Рутана. Чтобы выйти из этого заколдованного круга, В.А. Фок предложил решать уравнения (2.48) с помощью итерационной процедуры, которая получила название процедуры самосогласования. Сам метод Хартри-Фока часто называют методом самосогласованного поля ( ССП ). В соответствие с этой процедурой вначале выбирается некая приближенная матрица плотности и формируется начальный фокиан. Затем решаются уравнения (2.51) и находится новая (уже более точная) матрица плотности.

Процессу самосогласования посвящено большое количество специальных научных исследований. В настоящее время выработаны специальные алгоритмы (конвергеры), позволяющие ускорить сходимость процедуры ССП или добиться самосогласования для систем с плохой сходимостью. Наиболее простым методом является сдвиг виртуальных орбиталей на некоторую энергию dE вверх, так, что энергетическая щель между занятыми и виртуальными орбиталями увеличивается. Более сложным способом являются известные и часто применяемые процедуры DIIS и SOSCF, которые во многих случаях дают более высокое ускорение сходимости. Большинство современных квантовохимических программ позволяет произвольно использовать тот или иной конвергер по желанию пользователя. Следует, однако, помнить, что до настоящего времени нет универсальной процедуры, гарантирующей сходимость процедуры самосогласования во всех случаях.