 |
Главная |
Реализация симплекс-метода на примере
|
из
5.00
|
Продемонстрируем применение симплекс-метода на примере. Рассмотрим каноническую задачу ЛП
| f(x) = x1+ 2x2+0 x3+ 0 x4→max | (2.2) |
| –x1+ 2x2+ x3 = 4, | (2.3) |
| 3 x1+2x2 + x4 = 12, | (2.4) |
| xj ≥ 0, j = 1,2,3,4. | (2.5) |
Матрица условий A = (A1, A2, A3, A4), где
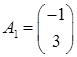
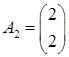
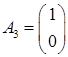
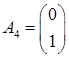
Целевой вектор c =(c1, c2, c3, c4) = (1, 2, 0, 0); вектор правых частей b=(b1, b2) = (4, 12).
Шаг 0. Нахождение начальной угловой точки (базисного плана).
Задача имеет предпочтительный вид, так как правые части уравнений положительны, а столбцы матрицы условий A3, A4 образуют единичную подматрицу. Значит начальная базисная матрица 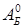 = (A3, A4); x3и x4 – базисные переменные, x1и x2 - небазисные переменные, cБ = (c3, c4) = = (0, 0).
= (A3, A4); x3и x4 – базисные переменные, x1и x2 - небазисные переменные, cБ = (c3, c4) = = (0, 0).
Начальный базисный план имеет вид x0 = (0, 0, x3, x4) = (0, 0, 4, 12); f( xo)= 0.
Шаг 1. Проверка базисного плана на оптимальность.
Подсчитаем симплексные оценки для небазисных переменных по формуле (5.1)
1 = < cБ, A1 > – c1 = 0 ·(–1) + 0 ·3 – 1 = –1.
2 = < cБ, A2 > – c2 = 0 ·2 + 0 · 2 – 2 = –2.
Так как оценки отрицательны, то план x – не оптимален. Будем искать новый базисный план (смежную угловую точку) с большим значением целевой функции.
Шаг 2. Нахождение переменной вводимой в базис.
Целевую функцию можно увеличить, если ввести в состав базисных переменных (сделать положительной) одну из небазисных переменных x1или x2, поскольку обе оценки j < 0. Обычно в состав базисных вводят небазисную переменную с наибольшей по модулю отрицательной оценкой, поэтому будем вводить в базис переменную x2.
Шаг 3. Определение переменной выводимой из базиса.
После ввода в базис переменной x2 новый план будет иметь вид
x' = (0, x2, x3, x4).
Этот план не является базисным, так как он содержит только одну нулевую координату, значит надо сделать нулевой (исключить из базиса) одну из переменных x3или x4. Подставим координаты плана x' = (0, x2, x3, x4) в ограничения задачи. Получим
2x2+ x3 = 4,
2x2 + x4 = 12.
Выразим отсюда базисные переменные x3и x4через переменную x2, вводимую в базис.
| x3 = 4 – 2x2, | (2.6) |
| x4 = 12 – 2x2. | (2.7) |
Так переменные x3и x4должны быть неотрицательны, получим систему неравенств
| 4 – 2x2 ≥ 0, | (2.8) |
| 12 – 2x2 ≥ 0. | (2.9) |
Чем больше значение x2, тем больше возрастает целевая функция. Найдем максимальное значение новой базисной переменной, не нарушающее ограничения задачи, то есть удовлетворяющее условиям (2.8), (2.9).
Перепишем последние неравенства в виде
2x2 ≤ 4,
2x2 ≤ 12,
откуда максимальное значение x2 = min { 4/2, 12/2 } = 2. Подставляя это значение в выражения (2.6), (2.7) для x3и x4,получаем x3 = 0.Следовательно x3 выводится из базиса.
Шаг 4. Определение координат нового базисного плана.
Новый базисный план (смежная угловая точка) имеет вид
x' = (0, x2, 0, x4)
Базис этой точки состоит из столбцов A2 и A4, так что 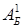 = (A2, A4). Этот базис не является единичным, так как вектор A2 = (2,2),и следовательно задача (2.2)–(2.5) не имеет предпочтительного вида относительно нового базиса. Преобразуем условия задачи (2.3), (2.4) таким образом, чтобы она приняла предпочтительный вид относительно новых базисных переменных x2, x4, то есть чтобы переменная x2входила в первое уравнение с коэффициентом, равным единице, и не присутствовала во втором уравнении. Перепишем уравнения задачи
= (A2, A4). Этот базис не является единичным, так как вектор A2 = (2,2),и следовательно задача (2.2)–(2.5) не имеет предпочтительного вида относительно нового базиса. Преобразуем условия задачи (2.3), (2.4) таким образом, чтобы она приняла предпочтительный вид относительно новых базисных переменных x2, x4, то есть чтобы переменная x2входила в первое уравнение с коэффициентом, равным единице, и не присутствовала во втором уравнении. Перепишем уравнения задачи
– x1+ 2 x2+ x3 = 4, (p1)
3x1 +2 x2 + x4 = 12. (p2)
Поделим первое уравнение на коэффициент при x2.Получим новое уравнение 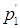 = p1 / 2, эквивалентное исходному
= p1 / 2, эквивалентное исходному
– 1/2 x1+ x2+ 1/2 x3 = 2. ( 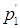 )
)
Используем это уравнение, которое назовем разрешающим, для исключения переменной x2из второго уравнения. Для этого надо уравнение  умножить на 2 и вычесть из p2. Получим
умножить на 2 и вычесть из p2. Получим 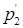 = p2 – 2
= p2 – 2 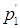 = p2 – p1:
= p2 – p1:
4 x1 – x3 + x4 = 8. ( 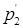 )
)
В итоге получили новое "предпочтительное" представление исходной задачи относительно новых базисных переменных x2, x4:
f(x) = x1 + 2 x2 + 0 x3 + 0 x4 max
– 1/2 x1+ x2+ 1/2 x3 = 2 ( 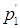 )
)
4 x1 – x3 + x4 = 8 ( 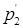 )
)
xj 0, j = 1,2,3,4
Подставляя сюда представление нового базисного плана x1 = (0, x2, 0, x4), сразу найдем его координаты, так как значения базисных переменных равны правым частям уравнений
x' = (0, 2, 0, 8); f(x1)=4.
На этом завершается первая итерация простого симплекс-метода. Далее процесс решения задачи продолжается с шага 1, состоящем в проверке найденного плана на оптимальность. Решение заканчивается тогда, когда все симплексные оценки текущего базисного плана окажутся неотрицательными.
Мы не будем проводить вторую итерацию по схеме первой, поскольку все вычисления симплекс-метода удобнее проводить в табличном виде.
|
из
5.00
|
Обсуждение в статье: Реализация симплекс-метода на примере |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

