Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики

Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории уравнений математической физики характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг уравнений математической физики с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование.

Классификация уравнений математической физики. Значительная часть уравнений математической физики составляют линейные уравнения с частными производными 2-го порядка общего вида:

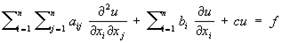,  (5)

где все коэффициенты a_ij (a_ij = a_ij), b_i, с и правая часть f представляют собой заданные функции независимых переменных x₁, x₂,.., х_п (n ³ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (5) существенно зависят от знаков корней (алгебраического относительно l) уравнения

= 0,   (6)

 и поэтому классификация уравнений (5) проводится в соответствии с этими знаками. Если все n корней уравнения (6) имеют одинаковый знак, то говорят, что уравнение (5) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (6) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты a_ij постоянны, то уравнение (5) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x₁,.., х_п, то и корни уравнения (6) зависят от x₁,.., х_п, а потому уравнение (5) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (5) сохраняется. Если корень уравнения (6), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).

Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.

Основные примеры уравнений математической физики.

Волновое уравнение

Волновое уравнение, дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде[1].

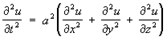
 – простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений.

В случае малых возмущений и однородной изотропной среды волновое уравнение имеет вид:

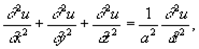
где х, у, z — пространственные переменные, t — время, u = u (х, у, z) — искомая функция, характеризующая возмущение в точке (х, у, z) в момент t, а — скорость распространения возмущения. Волновое уравнение является одним из основных уравнений математической физики и широко используется в приложениях. Если u зависит только от двух (одной) пространственных переменных, то волновое уравнение упрощается и называется двумерным (одномерным). Волновое уравнение допускает решение в виде «расходящейся сферической волны»:

u = f (t - r/a)/r,

где f — произвольная функция, a

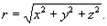
Особый интерес представляет так называемое элементарное решение (элементарная волна):

u = δ (t - r/a)/r

(где δ — дельта-функция), дающее процесс распространения возмущения, произведённого мгновенным точечным источником (действовавшим в начале координат при t = 0). Образно говоря, элементарная волна представляет собой «бесконечный всплеск» на окружности r = at, удаляющийся от начала координат со скоростью а с постепенным уменьшением интенсивности. При помощи наложения элементарных волн можно описать процесс распространения произвольного возмущения.

Малые колебания струны описываются одномерным В. у.:

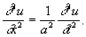
Ж. Д'Аламбер предложил (1747) метод решения этого В. у. в виде наложения прямой и обратной волн: u = f (x - at) + g (x + at), а Л. Эйлер (1748) установил, что функции f и g определяются заданием так называемых начальных условий.