 |
Главная |
Непрерывность функции.Точки разрыва функции и их классификация.
|
из
5.00
|
Свойства бесконечно малых
- Сумма конечного числа бесконечно малых — бесконечно малая.
- Произведение бесконечно малых — бесконечно малая.
- Произведение бесконечно малой последовательности на ограниченную — бесконечно малая.
2.Свойсва конечных пределов.
Теорема 2.8 Пусть функции 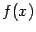 и
и 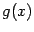 имеют пределы при одной и той же базе
имеют пределы при одной и той же базе  :
:
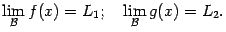
Тогда функция 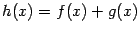 также имеет предел при базе
также имеет предел при базе  , и этот предел
, и этот предел  равен сумме пределов слагаемых:
равен сумме пределов слагаемых:
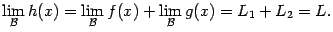
Доказательство. Равенство 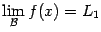 означает, в соответствии с теоремой 2.4, что величина
означает, в соответствии с теоремой 2.4, что величина 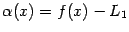 -- бесконечно малая; равенство
-- бесконечно малая; равенство  -- что
-- что 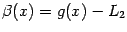 -- бесконечно малая. Поэтому по теореме 2.5 сумма
-- бесконечно малая. Поэтому по теореме 2.5 сумма
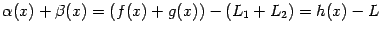
также является бесконечно малой. Теорема 2.4 утверждает, что тот факт, что разность 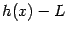 бесконечно мала, означает, что
бесконечно мала, означает, что 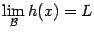 ; это и требовалось доказать.
; это и требовалось доказать.
Теорема 2.9 Пусть функции 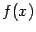 и
и 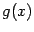 имеют пределы при одной и той же базе
имеют пределы при одной и той же базе  :
:
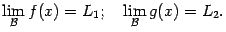
Тогда функция 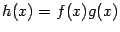 также имеет предел при базе
также имеет предел при базе  , и этот предел
, и этот предел  равен произведению пределов сомножителей:
равен произведению пределов сомножителей:
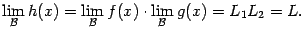
Доказательство. Равенство 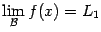 означает, в соответствии с теоремой 2.4, что величина
означает, в соответствии с теоремой 2.4, что величина 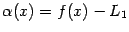 -- бесконечно малая; равенство
-- бесконечно малая; равенство  -- что
-- что 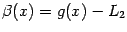 -- бесконечно малая. Поэтому
-- бесконечно малая. Поэтому 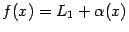 и
и 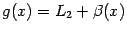 , откуда
, откуда
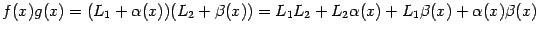
или
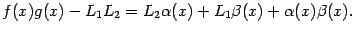
Покажем, что в правой части этого равенства стоит бесконечно малая величина. Величина 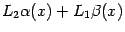 -- бесконечно малая согласно следствию 2.3, а величина
-- бесконечно малая согласно следствию 2.3, а величина  -- бесконечно малая по теореме 2.7 (величина
-- бесконечно малая по теореме 2.7 (величина 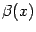 имеет предел, равный 0, и, следовательно, локально ограничена по теореме 2.6). Поскольку разность между функцией
имеет предел, равный 0, и, следовательно, локально ограничена по теореме 2.6). Поскольку разность между функцией 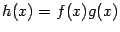 и постоянной
и постоянной 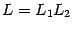 бесконечно мала при базе
бесконечно мала при базе  , то по теореме 2.4
, то по теореме 2.4 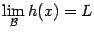 ; это и требовалось доказать.
; это и требовалось доказать.
3.Первый и второй замечательный предел. 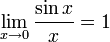
Доказательства 
Рассмотрим односторонние пределы 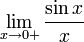 и
и 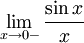 и докажем, что они равны 1.
и докажем, что они равны 1.
Пусть 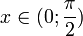 . Отложим этот угол на единичной окружности (R = 1).
. Отложим этот угол на единичной окружности (R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что: (1) 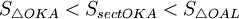 (где SsectOKA — площадь сектора OKA)
(где SsectOKA — площадь сектора OKA)
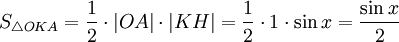
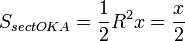
 (из
(из 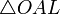 : | LA | = tgx)Подставляя в (1), получим:
: | LA | = tgx)Подставляя в (1), получим:
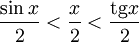 Так как при
Так как при 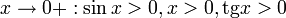
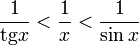 Умножаем на sinx:
Умножаем на sinx:
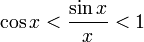 Перейдём к пределу:
Перейдём к пределу:

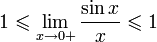
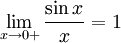
Найдём левый односторонний предел:
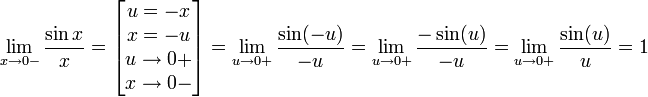
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
2 предел. 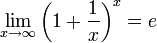
Непрерывность функции.Точки разрыва функции и их классификация.
Определение 3.1 Пусть функция 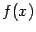 определена на некотором интервале
определена на некотором интервале  , для которого
, для которого 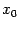 -- внутренняя точка. Функция
-- внутренняя точка. Функция 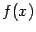 называется непрерывной в точке
называется непрерывной в точке 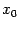 , если существует предел
, если существует предел 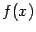 при
при 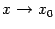 и этот предел равен значению
и этот предел равен значению 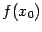 , то есть
, то есть
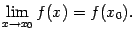
Точки разрыва. Точках=а наз точкой разрыва если в точке а эта фукция не определена либо определена но нарушено условие непрерывности. 1.точка устранимого разрыва. f(a-0)=f(a+0)≠f(a) 2.точка разрыва первого рода. f(a-0)≠f(a+0) 3.точка разрыва второго рода. Если в точке функция не имеет по крайне мере одного из односторонних пределов или хотя бы один из односторонних пределов равен бесконечности.
5.Определение производной и её геометрический смысл. Пусть в некоторой окрестности точки 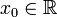 определена функция
определена функция 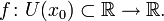 Производной функции f в точке x0 называется предел, если он существует,
Производной функции f в точке x0 называется предел, если он существует,
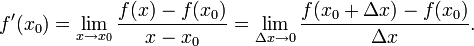
Геометрический смысл. Если функция 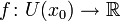 имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией
имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией
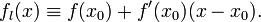
Функция fl называется касательной к f в точке x0. Число f'(x0) является угловым коэффициентом или тангенсом угла наклона касательной прямой.
6 Уравнения касательной и нормали (с выводом).
Касатаельной к графику ф-ции в точке Х0 является предельное положение секущей , при условии, что М->М0 k=tgβ; tgα= lim tgβ=lim AM/AM0= lim ∆y/∆x= y’(x0) ∆x->0 ∆x->0 ∆x->0 y’(x0)=tgα y-y0=k(x-x0) - уравнение прямой, проходящей через заданную точку с заданным коэффициентом k=tgα=f'(x0) y-f(x0)=f'(x0)(x-x0) y=f(x) уравнение касательной: y=f’(x0)(x-x0)+f(x0)=f(x0)+(f(x0)-f’(x0)x0)
Нормалью к графику функции y=f(x) в точке х0 называется прямая ⊥ касательной, проходящей через точку х0 Необходимое и достаточное условие перпендикулярности прямой : (l1⊥l2)<=>(k1= -1/k2) kn=1/f'(x0); a)f'(x0)≠0, б) f’(x0)=0 Уравнения нормали: а)y-f(x0)= (-1/f’(x0))*(x-x0);б)y=x0 y=(-1/f'(x0))+f(x0)+ x0/f'(x0)
7. таблица производных
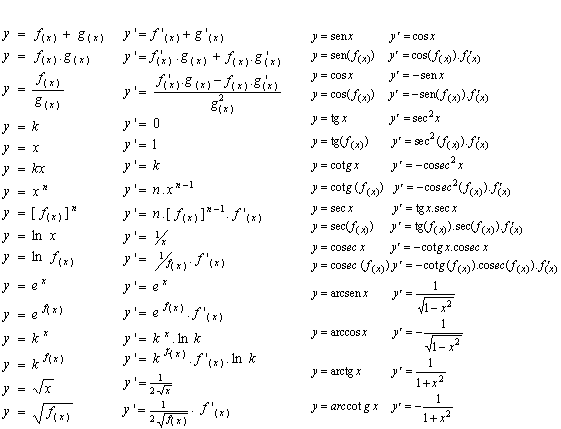
|
Вывод производных следующих функций: 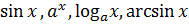 .!!!!!!!
.!!!!!!!



9. Определение дифференцируемости ф.Теорема о связи непрерывности с дифференцируемостью. Функция f(x) называется дифференцируемой в точке  , если её приращение в этой точке
, если её приращение в этой точке 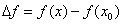 представимо в виде
представимо в виде 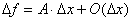 , где А – некоторая константа.
, где А – некоторая константа. 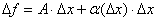 , где
, где 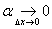 .Иначе говоря, функция f дифференцируема в точке
.Иначе говоря, функция f дифференцируема в точке  , если её приращение есть линейная функция относительно
, если её приращение есть линейная функция относительно  с точностью до бесконечно малых более высокого порядка, чем
с точностью до бесконечно малых более высокого порядка, чем  .
.
Теорема 4.1 Пусть функция 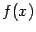 дифференцируема (дифференцируема слева, дифференцируема справа) в точке
дифференцируема (дифференцируема слева, дифференцируема справа) в точке 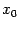 . Тогда
. Тогда 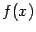 непрерывна (соотв. непрерывна слева, непрерывна справа) в этой точке
непрерывна (соотв. непрерывна слева, непрерывна справа) в этой точке 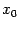 .
.
Доказательство. Из существования производной
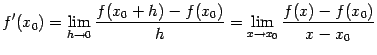
следует, что
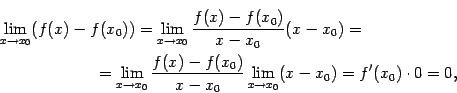
откуда

что и означает непрерывность функции 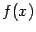 в точке
в точке 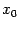 .
.
10.Определение дифференцируемости ф.Теорема о связи непрерывности с дифференцируемостью. Функция f(x) называется дифференцируемой в точке  , если её приращение в этой точке
, если её приращение в этой точке 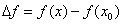 представимо в виде
представимо в виде 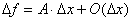 , где А – некоторая константа.
, где А – некоторая константа. 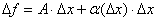 , где
, где 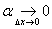 .Иначе говоря, функция f дифференцируема в точке
.Иначе говоря, функция f дифференцируема в точке  , если её приращение есть линейная функция относительно
, если её приращение есть линейная функция относительно  с точностью до бесконечно малых более высокого порядка, чем
с точностью до бесконечно малых более высокого порядка, чем  .
.
Для того чтобы ф-ция y=f(x) была дифференцируемой в точке x=x0, необходимо и достаточно существования в этой точке конечной производной f`(x0). При этом дельтаy = f`(x0)*deltax+alfa(deltax)*deltax
11.Дифференциал функции.Инвариантность формы дифф. Первого порядка.
Дифференциал 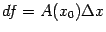 -- это главная, линейная по
-- это главная, линейная по 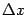 , часть приращения функции.
, часть приращения функции.
Пусть ф-ция y=f(x) дифференцируема в точке х, а ф-ция х=fi(u) некоторой независимой перменной u дифференцируема в соответствующей точке u. Тогда справедливо равенство: dy=f`(x)dx=f`(u)du
12.Свойства функций непрерывных на отрезке.Теоремы Ролля и Лагранжа. (1)Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.
(2) Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b]
(3)Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.
(4)Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b).
Теорема Ролля. Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю. Теорема Лагранжа. утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка 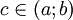 , что
, что 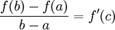 .Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
.Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
13.Правило Лопиталя для раскрытия неопределенностей вида 0/0 ∞/∞. Условия:
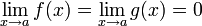 или
или 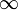 ; g(x) и f(x) дифференцируемы в проколотой окрестности a;
; g(x) и f(x) дифференцируемы в проколотой окрестности a;  в проколотой окрестности a; существует
в проколотой окрестности a; существует 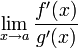 , тогда существует
, тогда существует 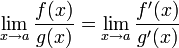 .Пределы также могут быть односторонними.
.Пределы также могут быть односторонними.
14.Теорема о производной сложной функции. Пусть  - функция, дифференцируемая в точке
- функция, дифференцируемая в точке 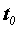 ,
, 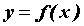 - функция, дифференцируемая в точке
- функция, дифференцируемая в точке 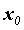 , причем
, причем 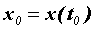 . Тогда
. Тогда 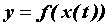 - сложная функция независимого переменного
- сложная функция независимого переменного 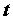 , дифференцируема в точке
, дифференцируема в точке 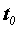 и ее производная в этой точке вычисляется по формуле
и ее производная в этой точке вычисляется по формуле 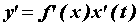
15.Монотонность функции на промежутке. Необходимые и достаточные условия. Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно.
Необходимое условие. Пусть функция 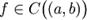 непрерывна на (a,b), и имеет в каждой точке
непрерывна на (a,b), и имеет в каждой точке 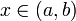 производную f'(x). Тогда
производную f'(x). Тогда
f возрастает на (a,b) тогда и только тогда, когда 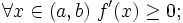
f убывает на (a,b) тогда и только тогда, когда 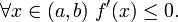
Достаточное условие. Пусть функция 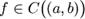 непрерывна на (a,b), и имеет в каждой точке
непрерывна на (a,b), и имеет в каждой точке 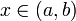 производную f'(x). Тогда
производную f'(x). Тогда
если 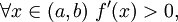 то f строго возрастает на (a,b);
то f строго возрастает на (a,b);
если 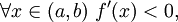 то f строго убывает на (a,b).
то f строго убывает на (a,b).
16.Экстремумы функций.Необходимые и достаточные условия. Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Необходимое условие. Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0), т.е. 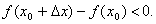 Но тогда
Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x0) ≥ 0 а при Δx → 0 + 0 f'(x0) ≤ 0. Так как f '(x0) определяет число, то эти два неравенства совместны только в том случае, когда f '(x0) = 0.
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль. Достаточное условие. Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x0 функция имеет максимум. Если же при переходе через x0 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Таким образом, если
- f '(x)>0 при x<x0 и f '(x)<0 при x> x0, то x0 – точка максимума;
-
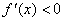 при x<x0 и f '(x)>0 при x> x0, то x0 – точка минимума.
при x<x0 и f '(x)>0 при x> x0, то x0 – точка минимума.
Доказательство. Предположим сначала, что при переходе через x0 производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x0 f '(x)>0 для x< x0, f '(x)<0 для x> x0. Применим теорему Лагранжа к разности f(x) - f(x0) = f '(c)(x- x0), где c лежит между x и x0.
- Пусть x < x0. Тогда c< x0 и f '(c)>0. Поэтомуf '(c)(x- x0)<0и, следовательно,
f(x) - f(x0)<0,т.е. f(x)< f(x0).
- Пусть x > x0. Тогда c> x0 и f '(c)<0. Значитf '(c)(x- x0)<0. Поэтому f(x) - f(x0)<0,т.е.f(x) < f(x0).
Таким образом, для всех значений x достаточно близких к x0 f(x) < f(x0). А это значит, что в точке x0 функция имеет максимум.
|
из
5.00
|
Обсуждение в статье: Непрерывность функции.Точки разрыва функции и их классификация. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

