Алгоритмы моделирования основных демодуляторов

Типовыми нелинейными операциями в радиосистемах являются операции модуляции, преобразования частоты (в том числе и умножения частоты) и демодуляции (детектирования). Для физического осуществления этих операций используются, как известно, различные нелинейные управляемые элементы совместно с фильтрами. Одним из принципов моделирования на ЦВМ нелинейных систем, осуществляющих указанные операции, с целью получения алгоритмов преобразования сигналов и помех в этих системах является воспроизведение на ЦВМ нелинейных уравнений, описывающих динамику рассматриваемых систем. При этом в зависимости от обстоятельств конкретной задачи могут быть использованы те или иные ранее описанные общие методы моделирования нелинейных систем.

В связи с тем, что задача разработки моделирующих алгоритмов по такому принципу ближе примыкает к вопросам математического обеспечения при использовании цифровых вычислительных машин для анализа нелинейных цепей, мы не будем останавливаться на подробностях ее решения.

Рассмотрим моделирование на ЦВМ типовых нелинейных преобразований радиосигналов и радиопомех, основанное на функциональном принципе.

Модуляция

Операции модуляции входят в математические модели радиосигналов и радиопомех. Поэтому воспроизведение на ЦВМ операций модуляции осуществляется, в сущности, при реализации цифровых моделей радиосигналов и радиопомех рассмотренные ранее.

Преобразование частоты

Назначением операций преобразования частоты является неискаженный перенос спектра сигнала с одной средней частоты ω₀ (несущей) на другую среднюю частоту ω_пр (промежуточную). С функциональной точки зрения такое преобразование, очевидно, сводится просто к замене в математической модели сигнала с частотой ω₀ сигналом с частотой ω_пр. При описании радиосистем по методу огибающих эта замена эквивалентна тождественному преобразованию. Если требуется с помощью ЦВМ исследовать более детальные изменения в сигналах, происходящие в конкретной схеме преобразователя частоты, например нелинейные искажения, появление дополнительных гармоник и т. п., то в этом случае нужно воспроизвести на ЦВМ цифровую модель нелинейной динамической системы, каковой является данный преобразователь частоты, используя описанные выше методы цифрового моделирования.

Детектирование

Рассмотрим теперь возможные способы моделирования нелинейных операций, осуществляемых над радиосигналами и помехами при различных видах детектирования, основанные на функциональном подходе и методе огибающих.

Пусть задан некоторый узкополосный процесс

(3.111)

в виде последовательности дискретных значений U[n] его комплексной амплитуды U(t) или же в виде последовательностей значений U₁[n] и U₂[n] его квадратурных компонент U₁(t)=Re U(t) и U₂(t) = ImU(t). Требуется найти алгоритмы, которые позволяли бы по известному дискретному комплексному процессу U[n] получать последовательности значений процессов U(t), φ_u(t), , выделяемых при различных видах идеального детектирования: амплитудного фазового и частотного. Такие алгоритмы легко предложить, используя известные формулы, выражающие параметры колебания (3.111) (амплитуду U(t) , фазу φ_u(t), частоту Ω(t) через комплексную огибающую U(t) и квадратурные составляющие U₁(t), U₂(t), а именно:

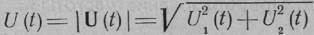
(3.112)

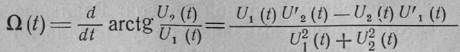
Подвергая формулы (3.112) дискретизации и заменяя при этом интеграл суммой, а производные — их первыми разностями, получим искомые алгоритмы:

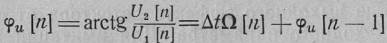
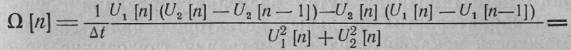
(3.113)

Следует сделать некоторые замечания к формулам (3.113). Эти формулы являются простыми алгоритмами преобразования дискретных квадратурных компонент узкополосного процесса в дискретные значения изменяющихся во времени параметров процесса, для выделения которых служат различные виды детекторов. Реальные детекторы реализуют преобразования (3.113) приближенно. Так, например, амплитудный детектор практически выделяет не саму огибающую U(t), а некоторую функцию от нее. Эта функция для детектора на вакуумном диоде при большом сопротивлении нагрузки хорошо аппроксимируется выражением

где I₀(x)—модифицированная функция Бесселя нулевого порядка. Реальный амплитудный детектор обладает также инерционностью. Аналогичным образом отличаются от идеальных реальные фазовые и частотные детекторы. У реального частотного детектора нелинейная зависимость выходного эффекта от частоты входного сигнала имеет вид дискриминационной кривой. Реальные фазовые детекторы обычно выделяют фазу сигнала по модулю 2π или π (приведенная фаза) и обладают нелинейностью. Все априорно известные отличия реальных детекторов от идеальных в случае необходимости нетрудно учесть при цифровом моделировании, подвергнув идеальные параметры, получаемые по формулам (3.113), нелинейному преобразованию в соответствии с нелинейной зависимостью выходного эффекта детектора от соответствующего входного параметра. Для имитации инерционности можно использовать линейный фильтр с соответствующей постоянной времени.

Достоинством алгоритмов идеального детектирования и алгоритмов, полученных на основе алгоритмов идеального детектирования путем введения коррекции с учетом характеристик реальных детекторов, является возможность исключить из рассмотрения трудоемкие операции нелинейных инерционных преобразований быстро осциллирующих функций и оперировать лишь с медленно меняющимися квадратурными компонентами детектируемых колебании.

Алгоритмы формирования дискретной фазы и дискретной частоты [вторая и пятая формулы из (1.113)] можно уточнить, если использовать более точные формулы численного интегрирования и дифференцирования. В приведенных формулах дискретные фильтры, осуществляющие дифференцирование и интегрирование, имеют простейшие передаточные функции соответственно:

В частности, повышенной точностью обладает оператор дискретного интегрирования

которому соответствует оператор дифференцирования

При использовании этих операторов алгоритмы формирования дискретной фазы и дискретной частоты запишутся в виде:

(3.114)

Где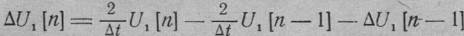

Рассмотрим еще одну распространенную операцию детектирования, а именно фазовое детектирование в случаях, когда в качестве опорного колебания в фазовом детекторе используется не чисто гармоническое колебание, а модулированное колебание

(3.115)

где Uoп (t) - комплексный закон модуляции опорного колебания (предполагается, что функция Uoп(t) медленно меняется по сравнению с e^jωt). Операцию фазового детектирования обычно можно представить как умножение входного колебания (3.111) на опорное колебание (3.115) с последующей фильтрацией низкочастотной составляющей спектра произведения. Такое представление позволяет найти простой алгоритм для моделирования фазового детектора. Действительно, при принятых условиях выходной эффект фазового детектора имеет вид

(3.116)

где черта сверху означает операцию выделения низкочастотной части спектра. Согласно известному тождеству

выражение (3.116) преобразуется к виду

(3.117)

Второе слагаемое в формуле (3.117) как высокочастотное отфильтровывается. Тогда, если положить, что первое низкочастотное слагаемое выделяется фильтром без искажений, окончательно получим

(3.118)

или в дискретной форме

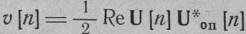(3.119)

Таким образом, операцию фазового детектирования можно рассматривать как выделение реальной части произведения комплексной амплитуды входного колебания на комплексно-сопряженную амплитуду опорного колебания. В частном случае, если опорное колебание не модулировано и его комплексная амплитуда равна 1 или e^jπ/2, фазовый детектор согласно формуле (3.118) выделяет квадратурные компоненты входного колебания

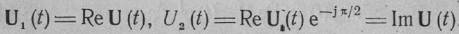(3.120)

Выражение (3.118) часто используется при описании процессов обработки сигналов в приемниках моноимпульсных радиолокаторов. Формулу (3.118) и алгоритм (3.119) можно использовать также для описания и цифрового моделирования процессов корреляционной обработки узкополосных сигналов. Для применения алгоритмов (3.113), (3.114) и (3.119) требуется знать квадратурные составляющие U₁(t) и U₂(t) или, что то же самое, комплексный закон модуляции U(t) детектируемого колебания u(t). При использовании метода огибающих для описания процессов в узкополосном преддетекторном фильтре квадратурные составляющие колебания u(t) оказываются известными непосредственно. Если же колебание u(t) задано последовательностью своих мгновенных значений, то для использования алгоритмов (3.113), (3.114) и (3.119) нужно каким-то образом, зная u(t), выделить его квадратурные компоненты U₁(t) и U₂(t). Для этой цели предлагается использовать следующий прием.

Рассмотрим аналитическое выражение колебания

функция sin ω₀t в моменты времени t_n = nΔt₀, где Δt₀= 2π/ω₀, равна нулю. В эти же моменты времени функция cos ω₀t равна единице, следовательно,

(3.121а)

Аналогично

(3.121б)

Иначе говоря, существуют последовательности равноотстоящих точек

t_n= nΔt₀ и t_n-1/4 = (n-1/4)Δt₀ оси времени, в которых графики функций u(t), U₁(t) и графики функций u(t), U₂(t) соответственно пересекаются. Этот факт иллюстрирует рис. 3.9 на примере частотно-модулированного по линейному закону радиоимпульса

(3.122)

где Т — длительность импульса; ΔΩ = 2πΔF — девиация частоты.

График построен для ΔΩ=ω₀/2 и ΔFТ=10 . Пунктиром даны квадратурные компоненты

Сигналы, показанные пунктиром, реально являются выходным эффектом при фазовом детектировании частотно-модулированного колебания (3.122) двумя фазовыми детекторами, у которых опорные колебания когерентны и сдвинуты но фазе на 90° (см. (3.120)]. Таким образом, для выделения дискретных квадратурных составляющих некоторого узкополосного процесса достаточно 'произвести выборки значений этого процесса в точках t_n= nΔt₀ и t_n-1/4 = (n-1/4)Δt₀. Поскольку квадратурные составляющие U₁(t), U₂(t) узкополосного процесса практически очень мало изменяются в течение четверти периода Δt₀, то в алгоритме (3.1216) можно приближенно считать

(3.123)

Тогда окончательный алгоритм выделения дискретных квадратурных составляющих можно записать в виде

(3.124)

Если погрешностью замены (3.123) пренебречь нельзя, значение U₂[n] можно уточнить, используя интерполяцию, например, между

Дл я увеличения точности алгоритмов дискретного выделения квадратурных составляющих имеется возможность уменьшения шага дискретизации вдвое по сравнению с Δt₀=2π/ω₀. При этом, как легко видеть,

(3.125)

Если шаг дискретизации Δt₀ весьма мал (при весьма узкополосном процессе), так что представление квадратурных составляющих оказывается излишне подробным, то можно увеличить шаг Δt₀ в целое число раз. Тогда алгоритм выделения квадратурных составляющих запишется в виде

(3.126)

Итак, для моделирования на ЦВМ операций детектирования узкополосного процесса u(t) согласно предложенному методу требуется два основных вида преобразований: выборка значений колебания u(t) в дискретных равноотстоящих точках по формулам (3.124) — (3.126) и вычисление дискретных последовательностей значений параметров этого колебания (амплитуды, фазы и т. д.) в соответствии с алгоритмами (3.113), (3.119).

Заканчивая рассмотрение данного метода, целесообразно сделать следующее замечание. Рассмотренные алгоритмы позволяют по имеющейся записи узкополосного процесса выделить в дискретной форме его заранее неизвестные законы модуляции. При этом должно быть точно зафиксировано начало отсчета времени, т. е. положение нуля на оси времени при модуляции и при детектировании должно быть одним и тем же. Реально это соответствует когерентному детектированию, когда в качестве опорного напряжения в фазочувствительных детекторах используется высокостабильная несущая. Оценим, к чему приведет детектирование по описанному методу при произвольном выборе начала отсчета времени, эквивалентном тому, что вместо точек фиксации t_n= nΔt₀ и t_n-1/4 = (n-1/4)Δt₀  мгновенных значений колебания u(t) берутся точки , где θ- произвольно взятое значение временного сдвига из интервала времени (0, Δt₀). Сдвиг точек фиксации равносилен замене колебания на входе цифрового детектора

колебанием

Поскольку функции U(t) и φ_u(t) медленно меняются по сравнению с cosω₀t, погрешностью за счет временного сдвига этих функций на величину, не большую периода несущей, практически можно пренебречь, т. е. можно считать, что

где φ₀=ω₀θ — случайная фаза, равномерно распределенная в интервале (0, 2π). Следовательно, цифровое детектирование по данному методу при произвольном выборе начала отсчета времени эквивалентно детектированию колебания с неизвестной (случайной) начальной фазой несущей частоты, что реально соответствует детектированию, когда в фазочувствительных детекторах вместо высокостабильной несущей в качестве опорного напряжения попользуется гармоническое колебание высокостабильного источника, независимого от генератора несущей. При таком детектировании амплитудные и частотные законы модуляции выделяются, очевидно, с той же точностью как и при строго когерентном детектировании, а фазовый закон модуляции может быть выделен лишь с точностью до постоянной составляющей φ₀.При детектировании колебаний со случайной равномерно распределенной начальной фазой нестабильность нуля времени, очевидно, никак не сказывается на статистических характеристиках выходного эффекта цифрового детектора.

 

Лекцию разработал

Доцент к.т.н. доцент       В. Ерохин

26.06.2014