Стохастика процессов эволюции

В процессах мутации и эволюции случайность играет решающую роль. Хотя эволюция в соответствующих физических условиях закономерна и необходима, все же в отдельных случаях она подвержена влиянию случайности. Именно поэтому только стохастическая теория может адекватно отражать сущность процессов эволюции. Существует, однако, и еще один аспект— дискретная природа молекулярных единиц процесса эволюции. В нормальных физических, химических и биологических процессах дискретной природой молекул можно пренебречь и перейти к описанию с помощью непрерывных концентраций. Однако в процессах мутации и эволюции один-единственный молекулярный акт — возникновение единственной молекулы нового сорта, обладающего теми или иными преимуществами, — может стать началом процесса макроскопического усиления, который приводит к полному изменению всей системы. Это основополагающее свойство эволюционирующих систем в литературе часто называется принципом усиления. Чтобы правильно описывать элементарный молекулярный акт эволюции, теория процессов мутации и эволюции должна была бы, по существу, следовать из квантовой теории систем с переменным числом частиц, например, выводиться из нее методом вторичного квантования. К сожалению, квантово-статистическая теория систем, в которых протекает химические реакции, делает в настоящее время лишь первые шаги. Полностью разработана только стохастическая теория реакций, на которую мы опираемся в дальнейшем.

В рамках стохастической теории реакций элементарным кинетическим актом авляется увеличение или уменьшение числа N_i молекул i-ro сорта на единицу, т.е.

 

N_i ® N_i ± 1.                                                   (7)

 

Состояние системы в момент времени t характеризуется множеством чисел заполнения для всех входящих в систему сортов: N₁(t), N₂(t), N₃(t), … .

Числа заполнения могут принимать только дискретные значения:

N_i = 0, l, 2, 3, … .

Здесь мы в основном рассматриваем системы, удовлетворяющие условию постоянства общего числа частиц

 

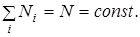                                 (8)

В пространстве чисел заполнения такие системы могут двигаться только по поверхности, определяемой условием (8). В силу сохранения числа частиц в элементарном переходе всегда участвуют два партнера:

 

N_i ® N_i + 1,             N_j ® N_j – 1.                                (9)

 

Пространство состояний и элементарные переходы в нем представлены на рис.6. Важная особенность рассматриваемых нами процессов эволюции по сравнению с процессами отбора, состоит в том, что при учете мутаций состояниями N_i = 0 можно пренебречь. Тем самым эти состояния утрачивают характер поглощающих состояний в пространстве состояний (рис. 6 и 7). Эта математическая ситуация выражает физически чрезвычайно важное обстоятельство, состоящее в том, что при мутации сорта N j > 0 может возникнуть новый сорт, который до этого вообще не был представлен в системе, т. е. до мутации должно выполняться равенство N_i = 0, а после мутации — равенство N_i = 1. С физической точки зрения, мутации всегда приводят к возникновению новых сортов молекул, не существовавших прежде в системе; с математической точки зрения, появление новых сортов соответствует расширению пространства состоянии за счет включения в него новых размерностей. Необходимо исходить из того, что пространство состояний макромолекулы имеет размерность порядка 10⁶⁰⁰. Так как во всей «Вселенной» число нуклонов достигает лишь 10⁷⁹, а из них можно построить не более чем 10⁷³ макромолекул, мы заключаем, что по крайней мере для 10⁵²⁷ размерностей должны выполняться равенства N_k = 0, или, иначе говоря, что представляющая точка состояния всегда должна лежать на одной из граней определяемой уравнениями симплициальной решетки. Таким образом, мутация означает, что представляющая точка удаляется от грани в новой, еще не занятой, размерности, а возникающий процесс отбора соответствует движению по новой грани при условии, что речь идет об инновации, т. е. о благоприятной мутации (рис. 7).

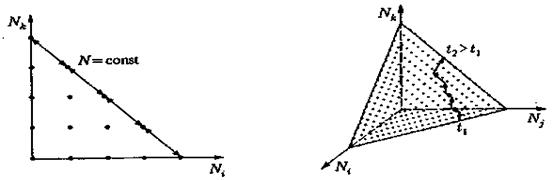
Рис.6 Пространство состояний и элементарные переходы в стохастическом процессе эволюции при постоянном числе (размерность 2)

Рис.7 Решетка-симплекс пространства состояний с примером траектории, образовавшейся после мутации.

 

Существует альтернативный вариант графического представления связанных с мутацией и отбором стохастических процессов в пространстве нуклеотидов, или последовательностей. В основе его лежит идея, предложенная Рехенбергом. Это представление исходит из того, что каждый нуклеотид в последовательности длиной v может находиться только в четырех состояниях: Г, А, Т, Ц. Для представления состояния такой последовательности можно воспользоваться v -мерным гиперкубом, состоящим в каждом направлении из трех «поставленных» один на другой элементарных кубов. На рис. 8 показан пример для случая v = 2.

 

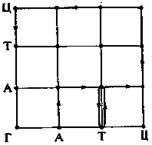
Рис. 8. Пространство нуклеотидов для последовательности пар и один из путей эволюции

 

Нетрудно видеть, что каждому из 16 состояний соответствует одна из пар-последовательностей ГГ, ГА, ГТ, ГЦ, АГ, АА, AT, АЦ, ТГ, ТА, ТТ, ТЦ, ЦГ, ЦА, ЦТ, ЦЦ — вершины прилегающих друг к другу квадратов. В случае последовательностей длины v = 3 необходимо включить еще тре тье измерение, в результате чего возникает куб с 64 вершинами, соответствующими 64 различным последовательностям-тройкам. Точковая мутация соответствует сдвигу вдоль ребра, параллельного одной из осей. Длины элементарных ребер не имеют непосредственного значения, так как априори все переходы Г → А, Г→ Т, Г → Ц, А → Т, А → Ц, А → Г, Ц → Г, Ц → А, Ц → Т равнозначны. Эволюционный nyi от одной последовательности нуклеотидов к другой, состоящий, вообще говор из многих мутаций, т. е. из многих шагов вдоль ребер, соответствует некоторок связному пути по гиперкубу. Примером может служить изображенный на рис. 8 эволюционный путь от АГ к ГТ. Если рассматривать популяции, то числу представителей Ni последовательности определенного типа i = А₁ ... А_v может бы сопоставлено скопление точек мощности N_i в непосредственной окрестности о ответствующей i вершины (или жирная точка). Эволюция популяции описываетcя блужданием скопления точек по пространству нуклеотидов. Графическое представление в пространстве нуклеотидов особенно удобно для наглядного истолкования путей эволюции и при обсуждении стратегий эволюции. На языке теории автоматов переходы в пространстве нуклеотидов могут быть описаны как процессы в автоматах Рабина-Скотга.

Подойдем теперь к определению вероятностей элементарных переходов (8) в единицу времени. При этом будем следовать более ранним работам, в которых вероятности переходов были получены сначала для более простых эволюционных процессов Эйгена, а позднее уточнены с учетом образования гиперциклов.

 

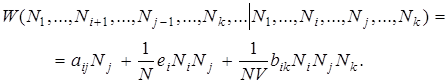         (9)

Здесь a_ij — входящие в выражение (9) скорости мутаций, е_i — скорости репродукции нуклеиновых кислот, b_ij — коэффициенты гиперциклических связей. Пренебрегая каталитическим действием протеинов, положим просто b_ij=0, е_i = E_i и a_ij = A_ij и получим бы вероятности перехода. Приведенные выше вероятности перехода позволяют легко вычислить стохастические траектории в пространстве состояний при заданных начальных условиях. Ценные выводы относительно исследуемого случайного процесса могут быть получены с помощью методов стохастической динамики, т. е. путем систематического исследования большого числа индивидуальных траекторий. Трудности, возникающие при применении этих методов к процессам эволюции, сводятся по существу с тому, что коэффициенты в выражении (8) известны лишь в очень грубом триближении. Другой метод исследования случайного процесса эволюции состоит в исследовании распределения вероятности

 

P(N₁,N₂, ...; t)                                                (9)

 

как функции времени. Для этого необходимо предварительно записать основное ;инетическое уравнение.

 

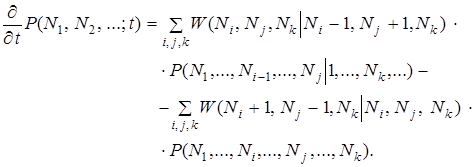             (10)

 

Распределение вероятности представляет собой поверхность, построенную над симплициальной решеткой; описанием деформации этой поверхности во времени служит случайный процесс эволюции. Разумеется, высказать определенное утверждение относительно распределения вероятности в пространстве столь высокой размерности необычайно трудно. К этому добавляется еще принципиальная трудность применения метода основного кинетического уравнения к общему эволюционному процессу: при заданных начальных распределениях, сосредоточенных на относительно узкой области пространства состояний (симплициальной решетки), основное кинетическое уравнение описывает систематическую тенденцию к относительно равномерному распределению вероятностей на всем пространстве состояний необычайно высокой размерности. Соответственно, возможные утверждения носят достаточно расплывчатый характер, а конечное стационарное распределение, к которому стремится система, по существу лишено определенного физического смысла. С другой стороны, основное кинетическое уравнение особенно хорошо подходит для изучения таких специальных вопросов, как выживание новых сортов и сосуществование новых сортов. Покажем, что основное кинетическое уравнение согласуется с детерминистическим уравнением . Для этого умножим уравнение (10) на N_k и просуммируем по всем числам заполнения. В результате мы получим уравнение для средних чисел заполнения:

 

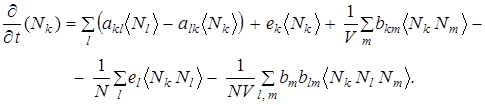(11)

 

Факторизуя средние значения и деля на объем, получаем из уравнения (11) уравнения для средней плотности X_k = (N_k)/V. Тем самым доказано, что стохастическое описание согласуется с детерминистическим. Исследуем теперь вопрос о вымирании или выживании нового сорта, возникающего в системе вследствие мутации. Ограничимся сначала простыми эйгеновскими системами без гиперцикцических связей. Предположим, что в системе имеется только один штаммовый сорт со скоростью воспроизведения Е₁ и только один представитель мутантов со скоростью воспроизведения E₂, т. е. в начальном состоянии t = 0 выполняются равенства N₁ = N - 1, N₂ = 1.

Условимся рассматривать N₂ как независимую переменную и пренебрегать в основном кинетическом уравнении всеми членами выше первой степени по N₂ (что вполне допустимо, если учесть начальные условия). В результате мы получим упрощенное уравнение

 

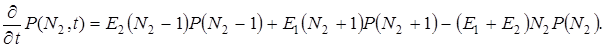(12)

 

Известно решение этого уравнения при начальном условии

 

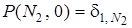                                  (13)

 

Если интересует вероятность вымирания мутанта по истечении времени t, то

 

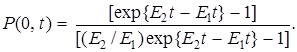(14)

 

Введем для удобства записи фактор преимущества

 

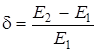                                         (15)

и найдем вероятность выживания нового сорта:

 

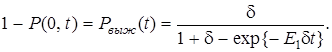    (16)

Если определить n = E_lt как меру числа поколений, которые выживают мутанты, то получится очень простая формула

 

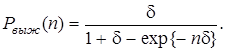                         (17)

 

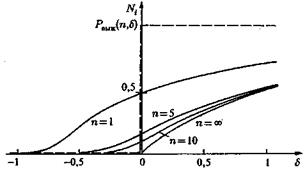
Рис. 9. Вероятность выживания мутанта через n поколений как функция фактора выживания d (сплошные линии — стохатическая теория; штриховые линии — детерминистическая теория)

 

На рис. 9 показана зависимость вероятности выживания от фактора преимущества и числа поколений. В то время как в детерминистической теории лучшие мутанты с d > 0 заведомо выживают, а худшие с d < 0 заведомо вымирают, более точная стохастическая теория предсказывает не столь определенное поведение. Как показано на рис. 9, вероятность выживания сначала возрастает с увеличением d, но подъем при d = 0 довольно плоский, вследствие чего примерно до n = 10 мутанты с d > 0 не очень существенно отличаются от d < 0. Мутанты, лежащие в определенной области (примерно в полосе ±10% от ценности штаммового сорта), в отношении отбора ведут себя почти нейтрально. Этим объясняется, почему в природе генотипы, представляющие вид, не едины, а охватывают группу сходных генных структур (дикий тип). Как показывает стохастическая теория, естественный отбор действует не очень точно, а допускает целое семейство генотипов, лежащих в области толерантности отбора.

Другое интересное утверждение, следующее из стохастической теории, состоит в том, что поведение гиперциклов типа «все или ничего» нарушается или по крайней мере ослабевает. Конкуренция между установившимся штаммовым гиперциклом и претерпевшим мутацию гиперциклом согласуется с динамическим поведением бистабильной системы. В детерминистической теории спонтанные переходы между двумя стабильными состояниями такой системы исключаются, стохастическая теория оставляет определенную вероятность таких переходов. Малость реакционного объема заведомо сыграла роль в ходе эволюции «протосупа». Примером тому служат реакции в коацерватах и в малых пылинках скальных пород. Решающий перелом к новому, лучшему гиперциклу в небольшом реакционном объеме мог произойти спонтанно и оттуда уже инфицировать макроскопическую окрестность.

Игра в имитацию

 

Одна из принципиальных трудностей при создании теории реального процесса эволюции состоит в том, что относительно значений входящих в теорию параметров, например, скоростей воспроизведения и мутаций, известно очень мало. Можно надеяться, однако, что новое направление экспериментальных исследований — проведение направленных эволюционных экспериментов на микроорганизмах — позволит получить новые данные. Ныне представляется разумным подвергнуть теорию проверке с помощью компьютерных экспериментов. Численные эксперименты не отражают полностью реальный процесс эволюции, но позволяют имитировать характерные особенности реальных процессов.

Начнем с изложения компьютерной модели Ферстерлинга, Куна и Тьюза. Речь идет о последовательностях длиной v = 9 из четырех букв А, Т, Г и Ц, постоянно воспроизводящихся, иногда с ошибками (мутациями), при условии постоянного общего числа частиц N = 50. Мы исходим из некоторой начальной случайной последовательности, например,

t = 0: N_i = 50, j = (ЦГТАТЦГТЦ).

 

Таким образом, процесс может начаться лишь с одной из S = 4⁹ = 262144 возможных последовательностей, т.е. процесс начинается с одной из вершин симплекса. Имеющиеся последовательности удваиваются по прошествии определенных интервалов времени. С помощью случайной программы в процессе удвоения с определенной вероятностью W при вписывании буквы совершается ошибка. Поcле каждого удвоения число последовательностей снова понижается до 50. Какая из последовательностей вымирает и какая выживает, решает случайная программа. При определении ценности последовательности авторы исходят из некоторой идеальной произвольно заданной последовательности, например, из последовательности

i = (АПТЦЦГАГ).

Путем сравнения с идеальной последовательностью i мы определяем число ошибочных мест F = d ( k , i ) в заданной последовательности k . Величина F указывает число несовпадений между последовательностями k и i. Ее можно рассматривать как метрическое расстояние между последовательностями. Ценность идеальной последовательности назначается произвольно. Для всех последовательностей с одной ошибкой ценность уменьшается в r раз, для всех последовательностей с двумя ошибками — в r² раз и т.д. Эти модельные предположения могут быть легко перенесены и в общий формализм, развитый в разд. 3. Модель Ферстерлинга, Куна и Тьюза соответствует стохастическому процессу на симплексе с N = 50 и вероятностями перехода

 

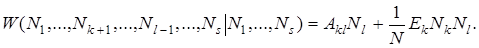  (19)

 

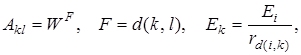Где                       (20)

i — заданная идеальная последовательность. В играх, проведенных Ферстерлингом, Куном и Тьюзом, r = 1,5, а частоты ошибок W = 0,0025; 0,01; 0,04. Некоторые результаты представлены в табл. 3. Во всех случаях система обнаруживала стремление к идеальной последовательности i, но с различным качеством и с различной скоростью. Благоприятной частотой ошибки оказалась величина W = 0,01: при таком значении W после 100 поколений 92% последовательностей достигают идеальной структуры, в то время как, например, при W = 0,04, подгонка идет очень плохо, а при W = 0,0025 процесс длится необычайно долго.

 

Таблица 3

Компьютерная модель процесса эволюции по Ферстерлингу, Куну и Тьюзу (а: W = 0,025, б: W = 0,01, в: W = 0,04)

Поколение	0			1			2			3			4			5			6
	а	б	в	а	б	в	а	б	в	а	б	в	а	б	в	а	б	в	а	б	в
0																50	50	50
10												11		4	29		42	6		4	4
20						1			12		14	33		23	4		12			1
30						6		5	34		45	9			1
40			4		3	10		34	23		13	13
50			19		14	17		36	13			1	47			3
60			18		23	19		26	12		1	1
70		1	15		33	25		15	10		1
80		14	29		31	17		5	3			1
90		41	30		8	13		1	7
100		46	33		4	15			1	49		1	1
110		47	28		3	20			2
120		41	30		9	16			3			1
130		49	28		1	16			5			1
150							49			1

 

Аналогичная компьютерная модель была исследована Эйгеном. Эйген рассматривал все последовательности длиной v = 20, которые можно составить из заглавных букв латинского алфавита, знаков препинания и пробелов u. В качестве идеальной последовательности он выбрал осмысленную фразу «На ошибках учимся»:

LE R N u A U S u D E N u F E H L E R N.

Компьютер работал не непосредственно с буквами алфавита, а предварительно переводил их в последовательности двоичных знаков 0 и 1 (поскольку 2⁵ = 32, для кодирования одной буквы требуется 5 двоичных знаков). В двоичном алфавите идеальная последовательность принимает следующий вид:

10001010101011110011001010011011010110000010101001 01010100110010101011010100110110001010101011110011

В этом пространстве двоичных последовательностей длины v =100 разыгрывается игра отбора. При этом рассматриваются только 10 копий, т. е. стохастический процесс протекает на симплексе с N = 10. Всего существует S = 2¹⁰⁰ альтернативных последовательностей. Определим для произвольной последовательности k число F = d ( k , i ) несовпадений с приведенной выше идеальной последовательностью. Как и в предыдущем примере, ценность реальной последовательности k убывает с увеличением отклонения от идеальной последовательности по закону

 

E_k = E_i r ^–F = E_i r ^–d(k,i).                                    (21)

 

В конкретной модели Эйген ( Eigen , 1976) выбрал r = 2,7, а скорость мутаций определил с помощью соотношения

 

A_kl = (1 – q)^{d ( k , l )}.                                             (22)

 

Здесь q — вероятность правильного вписывания одной буквы, и, соответственно, W = 1 - q — вероятность ошибки.

Таблица 4

Компьютерная модель процесса эволюции по Эйгену

Поколение	Частота ошибки	Лучшая последовательность	Частота
0	0,001	KORN AUS DEN FELDERN	10
32	0,001	KORN AUS DEN FELDERN	9
69	0,001	LURN AUS DEN FEXLERN	7
0	0,01	KORN AUS DEN FELDERN	10
1	0,01	KSRN AUS DEN FEL?ERN	1
11	0,01	LERN AUS DEN FEHLERN	1
15	0,01	LERN AUS DEN FEHLERN	3
32	0,01	LERN AUS DEN FEHLERN	4
0	0,02	KORN AUS DEN FELDERN	10
23	0,02	LERN IUS DER FEHLER	1
0	0,03	KORN AUS DEN FELDERN	10
11	0,03	?ARA GUY??!NCVEHTUNA	1

 

В табл. 4 представлены результаты проведенной Эйгеном игры. Приведенные данные позволяют прийти к следующим выводам.

1. Слишком малые частоты ошибок медленно формирует эволюционный процесс, частота прогресса остается малой.

2. Слишком высокие частоты ошибок приводят к разрыву последовательностей. Это происходит, как только превышается некий порог ошибки, определяемый множеством символов.

3. Благоприятные условия для эволюции соответствуют уровню, лежащему чуть ниже этого порога.

В той же работе Эйген исследовал интересную модель с гиперциклическими связями между воспроизводящимися последовательностями. Определенный недостаток компьютерных моделей, исследованных Ферстерлингом, Куном и Тыозом, а также Эйгеном, состоит в том, что должна быть задана «цель эволюции» — идеальная последовательность. Разумеется, для реальных процессов эволюции идеальная последовательность, если она вообще существует, не задана. Существование априорно заданной цели эволюции сделало бы излишним сложный и сопряженный с большими затратами процесс поиска, поскольку был бы известен кратчайший путь к достижению цели. Именно поэтому представляют интерес модели эволюции, которые не исходят из предположения о существовании заданной идеальной последовательности. Такие модели были развиты в более давних работах. Изложим наиболее существенные особенности этих моделей.

Рассмотрим последовательности из букв А, В, С и D длиной до 20 букв, т.е. 1 £ v £ 20, S = 4 + 4² + 4³ + ... + 4²⁰ ≈ 10¹².

Приведем несколько примеров таких последовательностей

A, DA, DAC, DABC, BDADB.

Общее число возможных последовательностей S необычайно велико. Компьютерная игра проводится на симплексе N = 100. Стохастические переходы на симплексе происходят по правилам, вытекающим из общего соотношения (55). Технически каждая последовательность хранится в сжатом виде в «регистре» длиной в 20 символов. Например, две последние последовательности хранятся в форме

DABC0000000000000000, BDADB000000000000000.

Каждой из 100 участвующих в игре последовательностей следует поставить в соответствие такой «регистр». Опишем теперь процесс мутации, состоящий либо в перестановке отдельных букв, либо в обрыве какой-то из начинающейся слева последовательности символов. Алгоритм мутации в компьютерной игре состоит из следующих правил.

1. Вписать в одну из ячеек любого из 100 регистров одну из четырех букв А, В, С, D или нуль.

2. Переставить циклически все ячейки, т. е. расположить их в таком порядке, чтобы ячейка 1 шла за ячейкой 2, ячейка 2 — за ячейкой 3,..., ячейка 20 — за ячейкой 1.

3. Вычеркнуть все нули и все части последовательности, стоящие справа от нуля. Возникающая после этих операций последовательность представляет собой результат мутации.

Нетрудно видеть, что в этой игре перестановка буквы в 20-ю ячейку эквивалентна приписыванию этой буквы к левому концу последовательности. Возможны также и перестановки буквы в нулевую позицию справа от последовательности или приписывание буквы к правому концу последовательности. Таким образом, алгоритм мутации допускает удлинение и сокращение цепей с обеих сторон. Для оценки каждой последовательности произвольно устанавливается код из перекрывающихся дублетов. Исходные позиции А, В, С, D оцениваются величиной w = 1, 2, 3, 4, а каждая последующая позиция оценивается в зависимости от ее ближайшего соседа по следующей таблице:

 

AA w : = w,	CA w : = w / 3,
AB w : = w,	CB w : = w + q / 3,
AC w : = w + 1,	CC w : = w,
AD w : = w / q,	CD w : = w / 3,
BA w : = w + q / 2,	DA w : = w + 4 / q,
BB w : = w,	DB w : = w / 4,
BC w : = w /2,	DC w : = w + q / 4,
BD w : = w + 2,	DD w : = w.

 

Если p — позиция первой буквы дублета, то q = p – g[(p - 1) / g], где квадратные скобки обозначают целую часть числа. Приведем несколько примеров:

 

w(DAC) = 4 + 4 + 1 = 9,

w(DACBA) = 4 + 4 + 1 + 1 + 2 = 12,

w(BDADBBA) = (2 + 2 + 4/2) • (1/3) • (1/4) • 1 + 6/2 = 3,5.

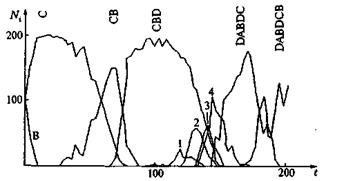
Рис. 10. Компьютерная реализация стохаcтического процесса отбора (тип 1) с частотой мутаций 0,01 на репликацию и признак (1 — СВDD; 2 — CBDDC; 4 — CBDDCB)

 

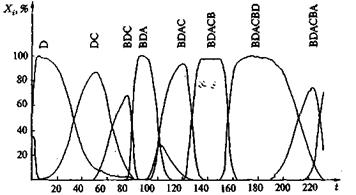
Рис. 11. Компьютерная реализация детерминистического процесса отбора со стохатическим появлением мутаций с частотой 0,03 на репликацию и признак (тип 1)

 

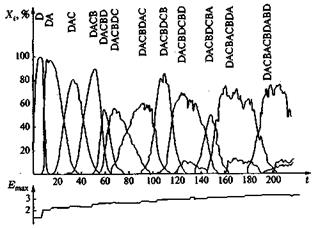
Рис. 12. Компьютерная реализация детерминистического процесса отбора со стохатическим появлением мутаций с частотой 0,1 на репликацию и признак (тип 1)

 

На рис. 10, 11 и 12 представлены три различных примера компьютерных реализаций эволюционного процесса при различных частотах мутации. Отчетливо видно, как в игру эволюции вступают новые, более приспособленные сорта, доминируют в течение какого-то периода и затем уступают место еще лучшим сортам. При таком процессе длина цепи постоянно растет, и образуются характерные структуры. На рис. 13 показано несколько путей эволюции, по которым могло бы пойти развитие системы. Возникает характерное дерево эволюции со все более сильно ветвящейся кроной. На рис. 13 представлена лишь часть возможных маршрутов, соответствующих наиболее часто проходимым ветвям. В действительности к последовательностям ведут 262 144 ветвей. Усиливающееся ветвление является характерной особенностью рассматриваемой модели, в то время как модели Ферс-терлинга, Куна и Тьюза, а также Эйгена, основанные на задании идеальной последовательности (цели эволюции), должны сходиться к этой последовательности, В нашей модели процесс протекает на ветви дерева, которая ветвится все чаще по мере подъема от корня дерева. Переход между различными ветвями дерева вследствие глубоких провалов между соответствующими селекционными ценностями относительно маловероятен, но отнюдь не исключаются полностью. Из-за многочисленных ветвей система, как правило, не может достигнуть вершины дерева, так как с высокой вероятностью вершина не лежит на той ветви, по которой происходит эволюция системы. Тенденция направлена на достижение относительного преимущества, эволюция протекает под девизом «все выше и выше», но никакой заранее заданной цели процесса не существует.

Если эволюция последовательностей в моделях Ферстерлинга и др. (и Эйгена происходит при фиксированной длине цепей, то «высота» на основе нашей системы оценок связана с увеличением длины последовательностей. Поэтому в нашей модели изменяется процентное отношение (доля) ошибочных копий, т.е. как E _i, так и Q _i, изменяют свое значение от последовательности к последовательности.

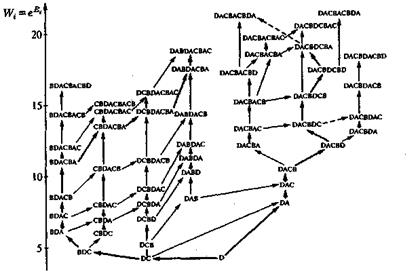
Рис. 13. Дерево эволюции на основе дублетов (тип 1) (жирными стрелками показан путь эволюции, пройденный при компьютерной реализации)

 

Это отчетливо видно на рис. 14: с увеличением длины возрастает как селекционная ценность E _i, так и число производимых мутантов соответствующей штаммовой последовательности. Последнее выражается в том, что более длинные последовательности образуются только в меньших стационарных концентрациях и что заметно возрастает стохастическое влияние мутаций (в случае коротких последовательностей кривые идут весьма гладко, а с увеличением длины становятся все более извилистыми). Этот процесс продолжается до тех пор, пока не будет достигнута определяемая выражением (4) максимальная длина; она соответствует некоторой исчезающе малой стационарной концентрации. Эволюция не останавливается по достижении оптимальной последовательности с максимально возможной длиной, процесс завершается «мутационной катастрофой». Возникает спектр последовательностей, ни одна из которых не образуется с устойчивой частотой. Нестабильность частот связана с приближением к эйгеновской предельной длине (4). Чтобы достичь надежной репликации длинных последовательностей, частота ошибки на одну букву должна убывать обратно пропорционально длине последовательности. Известно, что в пребиологической эволюции повышение точности репликации, например, в результате появления репликаз, должно было иметь центральное значение.

 

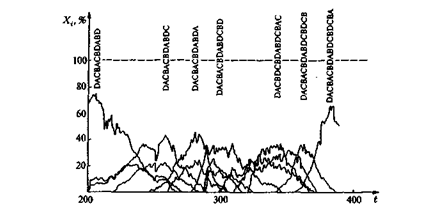Рис. 14. Мутационная катастрофа: продолжение процесса, начало которого представлено на рис.12, приводит к хаотическому распределению последовательностей

 

В игре в имитацию типа II учитывается необходимое повышение точности репликации и вместо фиксированной частоты мутации MR используется переменную частоту мутации

 

.

 

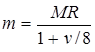Затем в этой игре в имитацию исследованию подлежит новый «фрустированный» тип вычисления значений. Очень простое по сравнению с типом I правило имеет следующий вид:

E _i = w_i ,                                                 (23)

 

где w = 1, 2, 3, 4 надлежит подставить вместо букв A, B, C, D на первом месте по следующему алгоритму:

 

IF а§(р ТО р + 1) = АВ, ВС, CD, DA     LET w: = w + l,

IF a§(p) = a§(p + g)                        LET w : = w + b.

Этот «рецепт» ставит каждой паре букв, расположенных в алфавитном порядке, приращение текущего значения на одну единицу (пара букв DA считается расположенной в алфавитном порядке), а периодичности длиной g — приращение b. В то время как в игре в имитацию типа I сложность последовательности в конечном счете следует из сложности правил вычисления значения, при игре в имитацию типа II она следует из сложности правил вычисления только в том случае, если два простых частичных правила противоречат друг другу (фрустрация).

Первое из двух частичных правил отдает предпочтение последовательностям типа DABCDABCDABCDABCDABC ...,

в то время как второе частичное правило отдает предпочтение последовательностям с периодом g. При g ¹ 4 может быть выполнено лишь одно из двух требований, предъявляемых к оптимальности. Например, если положить g = 5, то после 4-й позиции образуется ошибочный порядок, например, DABCCDABCCDABCCDABCC....

Если длина равна 20, то период 4 имеет значение w = 23, а период 5 с ошибочным порядком — значение w = 19 + 15b. Критическое значение для доминирования одного или другого правила определяется величиной

 

 

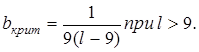
или в случае длинных последовательностей — величиной b_крит = 1/g. Для генерирования более сложных последовательностей параметр b полезно поддерживать на критическом значении: b = b_крит. Это позволяет достигать максимального эффекта фрустрации