 |
Главная |
Геометрическая иллюстрация
|
из
5.00
|
Вывод формулы Симпсона
Если для каждой пары отрезков 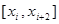 построить многочлен второй степени, затем проинтегрировать его и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона.
построить многочлен второй степени, затем проинтегрировать его и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона.
 Рассмотрим подынтегральную функцию
Рассмотрим подынтегральную функцию 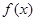 на отрезке
на отрезке 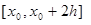 . Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с
. Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с 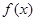 в точках
в точках 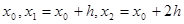 :
:
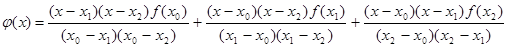
Проинтегрируем 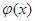 :
:
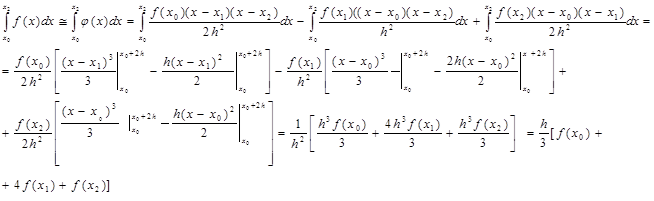
Формула:
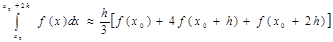
и называется формулой Симпсона.
Полученное для интеграла  значение совпадает с площадью криволинейной трапеции, ограниченной осью
значение совпадает с площадью криволинейной трапеции, ограниченной осью 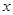 , прямыми
, прямыми 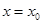 ,
,  и параболой, проходящей через точки
и параболой, проходящей через точки 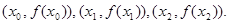
Оценим теперь погрешность интегрирования по формуле Симпсона. Будем считать, что у 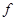 на отрезке
на отрезке 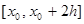 существуют непрерывные производные
существуют непрерывные производные 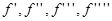 . Составим разность
. Составим разность
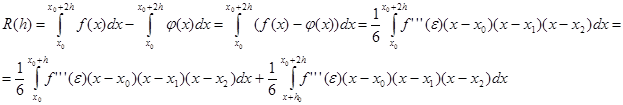
К каждому из этих двух интегралов уже можно применить теорему о среднем, поскольку 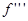 непрерывна на
непрерывна на 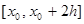 и функция
и функция  неотрицательна на первом интервале интегрирования и неположительна на втором ( то есть не меняет знака на каждом из этих интервалов). Поэтому:
неотрицательна на первом интервале интегрирования и неположительна на втором ( то есть не меняет знака на каждом из этих интервалов). Поэтому:
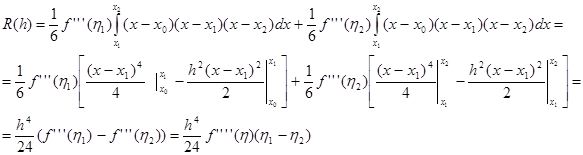
(мы воспользовались теоремой о среднем, поскольку 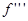 - непрерывная функция;
- непрерывная функция;  ).
).
Дифференцируя 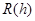 дважды и применяя затем теорему о среднем, получим для
дважды и применяя затем теорему о среднем, получим для 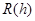 другое выражение:
другое выражение:
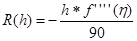 , где
, где 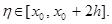
Из обеих оценок для 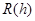 следует, что формула Симпсона является точной для многочленов степени не выше третьей. Запишем формулу Симпсона, напрмер, в виде:
следует, что формула Симпсона является точной для многочленов степени не выше третьей. Запишем формулу Симпсона, напрмер, в виде:
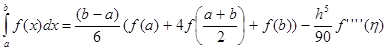 ,
, 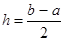 .
.
Если отрезок 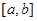 интегрирования слишком велик, то его разбивают на
интегрирования слишком велик, то его разбивают на 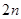 равных частей (полагая
равных частей (полагая 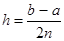 ), после чего к каждой паре соседних отрезков
), после чего к каждой паре соседних отрезков 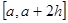 ,
, 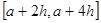 ,...,
,..., 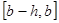 применяют формулу Симпсона, именно:
применяют формулу Симпсона, именно:
Запишем формулу Симпсона в общем виде:
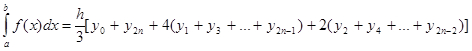 (1)
(1)
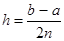 (2)
(2)
Погрешность формулы Симпсона - метода четвертого порядка:
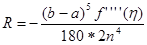 ,
, 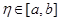 (3)
(3)
Так как метод Симпсона позволяет получить высокую точность, если 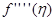 не слишком велика. В противном случае метод второго порядка может дать большую точность.
не слишком велика. В противном случае метод второго порядка может дать большую точность.
Например, для функции 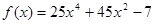 форма трапеции при
форма трапеции при 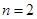 для
для  дает точный результат
дает точный результат 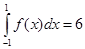 , тогда как по формуле Симпсона получаем
, тогда как по формуле Симпсона получаем 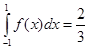
Геометрическая иллюстрация
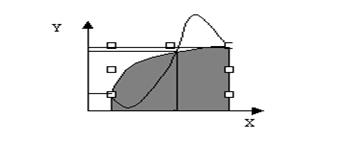 |

На отрезке 
 длиной 2h строится парабола, проходящая через три точки
длиной 2h строится парабола, проходящая через три точки 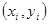 ,
, 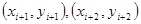 . Площадь под параболой, заключенная между осью OX и прямыми
. Площадь под параболой, заключенная между осью OX и прямыми 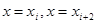 , принимают равной интегралу
, принимают равной интегралу 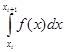 .
.
Особенностью применения формулы Симпсона является тот факт, что число разбиений отрезка интегрирования - четное.
Если же количество отрезков разбиения - нечетное, то для первых трех отрезков следует применить формулу, использующую параболу третьей степени, проходящую через четыре первые точки, для аппроксимации подынтегральной функции.
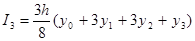 (4)
(4)
Это формула Симпсона «трех восьмых».
Для произвольного отрезка интегрирования 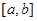 формула (4) может быть «продолжена»; при этом число частичных отрезков должно быть кратно трем (
формула (4) может быть «продолжена»; при этом число частичных отрезков должно быть кратно трем ( 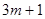 точек).
точек).
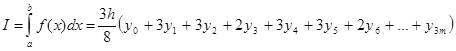
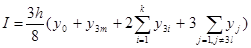 , m=2,3,... (5)
, m=2,3,... (5)
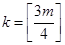 - целая часть
- целая часть
Можно получить формулы Ньютона-Котеса старших порядков :
 (6)
(6)
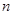 - количество отрезков разбиения;
- количество отрезков разбиения;
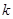 - степень используемого полинома;
- степень используемого полинома;
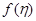 - производная
- производная 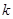 -го порядка в точке
-го порядка в точке  ;
;
 - шаг разбиения.
- шаг разбиения.
В таблице 1 выписаны коэффициенты 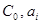 . Каждая строка соответствует одному набору
. Каждая строка соответствует одному набору 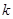 промежутков
промежутков 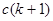 узлами для построения многочлена k-ой степени. Чтобы воспользоваться этой схемой для большего количества наборов (например, при k=2 и n=6), нужно «продолжить» коэффициенты, а затем сложить их.
узлами для построения многочлена k-ой степени. Чтобы воспользоваться этой схемой для большего количества наборов (например, при k=2 и n=6), нужно «продолжить» коэффициенты, а затем сложить их.
Таблица 1:
| k | C0 | A0 | a1 | a2 | a3 | a4 | a5 | a6 | |
| 2 | 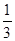
| 1 | 4 | 1 | |||||
| 1 | 4 | 1 | |||||||
| 1 | 4 | 1 | |||||||
| 1 | 4 | 2 | 2 | 4 | 1 | å |
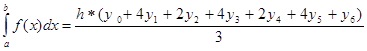
Алгоритм оценки погрешности формул трапеции и Симпсона можно записать в виде: 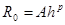 (7),
(7),
где 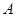 - коэффициент, зависящий от метода интегрирования и свойств подынтегральной функции;
- коэффициент, зависящий от метода интегрирования и свойств подынтегральной функции;
h - шаг интегрирования;
p - порядок метода.
Правило Рунге применяют для вычисления погрешности путем двойного просчета интеграла с шагами h и kh.
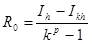 (8)
(8)
(8) - апостериорная оценка. Тогда Iуточн.=  +Ro (9),
+Ro (9), 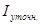 уточненное значение интеграла
уточненное значение интеграла 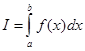 .
.
Если порядок метода неизвестен, необходимо вычислить I в третий раз с шагом 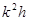 , то есть:
, то есть:
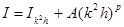
из системы трех уравнений:
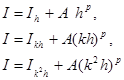
с неизвестными I,А и p получаем :
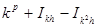 (10)
(10)
Из (10) следует 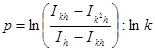 (11)
(11)
Таким образом, метод двойного просчета, использованный необходимое число раз, позволяет вычислить интеграл с заданной степенью точности. Выбор необходимого числа разбиений осуществляется автоматически. Можно при этом использовать многократное обращение к подпрограммам соответствующих методов интегрирования, не изменяя алгоритмов этих методов. Однако для методов, использующих равноотносящие узлы, удается модифицировать алгоритмы и уменьшить вдвое количество вычислений подынтегральной функции за счет использования интегральных сумм, накопленных при предыдущих кратных разбиениях интервала интегрирования. Два приближенных значения интеграла 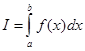
 и
и 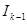 , вычисляемые по методу трапеции с шагами
, вычисляемые по методу трапеции с шагами 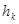
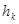 и
и 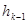 , связаны соотношением:
, связаны соотношением:
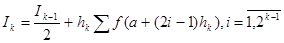
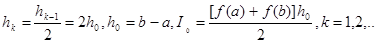 (12)
(12)
Аналогично, для интегралов, вычисленных по формуле с шагами 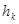 и
и 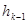 , справедливы соотношения:
, справедливы соотношения:
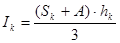 ,
, 

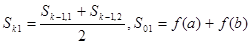 (13)
(13)
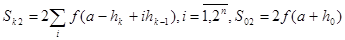
|
из
5.00
|
Обсуждение в статье: Геометрическая иллюстрация |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

