 |
Главная |
ЛАБОРАТОРНАЯ РАБОТА № 2. ИЗУЧЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ СЛУЧАЙНЫХ ЧИСЕЛ
|
из
5.00
|
1 Цель работы
1. Изучить принципы тестирования последовательностей случайных чисел.
2. Получить последовательность случайных чисел с помощью КГСЧ и исследователь ее на случайность с помощью методов корреляционного анализа.
3. Изучать принцип работы программы RandomTest и протестировать последовательность случайных чисел с помощью алгоритмов NIST.
4. Регулирую ток через светоизлучающий диод и напряжение на кремниевом фотоэлектронном умножителе получить последовательность случайных чисел, которая будет удовлетворять всем описанным в лабораторной работе тестам.
2 Краткие теоретические сведения
2.1. Назначение и сущность генераторов случайных чисел и проверки случайных последовательностей
Потребность в случайных и псевдослучайных числах возникает во многих криптографических задачах. Например, обычные криптосистемы используют ключи, которые должны генерироваться случайным образом. Многие криптографические протоколы также требуют случайных или псевдослучайных входов в различных точках, например, для вспомогательных величин, используемых при генерации цифровых подписей, или для усложнения в протоколах аутентификации и дополнительная защита от взлома.
Данные последовательности могут использоваться для получения криптографических ключей, например, пароль пользователя в системе, предварительно будут преобразованы в base64 – стандарт кодирования двоичных данных при помощи только 64 символов ASCII. Он содержит текстово-цифровые латинские символы A-Z, a-z и 0-9 (62 знака) и 2 дополнительных символа, зависящих от системы реализации (например, «+» и «/»). В основе алгоритма лежит сведение трех восьмерок битов (24) к четырем шестеркам (тоже 24) и представление этих шестерок в виде символов ASCII. Таким образом получается обратимое шифрование, единственным недостатком которого будет увеличивающийся при кодировании размер — в соотношении 4:3.
Существует два основных типа генераторов, используемых для создания случайных последовательностей: генераторы случайных чисел (физические) и генераторы псевдослучайных чисел (программные) [1]. Для криптографических приложений оба этих типа генераторов создают последовательность нулей и единиц, которые могут быть разделены на потоки или блоки случайных чисел. Физические ГСЧ принимают на вход некий случайный бесконечный процесс, а на выходе дают бесконечную (зависит от времени наблюдения) последовательность 0 и 1. Программные ГСЧ представляют собой заданную разработчиком детерминированную функцию, которая инициализируется так называемым зерном, после чего также на выходе выдает последовательность 0 и 1. Зная это зерно, можно предсказать всю последовательность. Следовательно, по умолчанию программный ГСЧ должен получать свои начальные значения из выходов физического [2].
Хороший программный ГСЧ – это тот, для которого невозможно предсказать последующие значения, имея всю историю предыдущих значений, не имея зерна. Такое свойство называется прямой непредсказуемостью.
Физические ГСЧ имеют также проблемы:
· случайное явление, которое берется за основу, может быть не способно выдавать числа с нужной скоростью;
· с виду случайные явления могут быть не такими случайными. Например, электромагнитный шум может быть суперпозицией нескольких более-менее однообразных периодических сигналов;
· со временем возможно изменение параметров ГСЧ [1].
Влияние этих проблемы может быть снижено путем объединения выходов из различных типов источников для использования в качестве входов для ГСЧ. Однако полученные результаты от ГСЧ могут все еще быть недостаточными при оценке статистическими тестами. Кроме того, производство высококачественных случайных чисел может быть слишком трудоемким, что делает такое производство нежелательным, когда необходимо большое количество случайных чисел. Для получения большого количества случайных чисел могут быть предпочтительны генераторы псевдослучайных чисел [3].
Псевдослучайные числа часто оказываются более случайными, чем случайные числа, полученные из физических источников. Если псевдослучайная последовательность построена правильно, каждое значение в последовательности получается из предыдущего значения с помощью преобразований, которые вносят дополнительную случайность. Ряд таких преобразований может устранить статистические автокорреляции между входом и выходом. Таким образом, выходные данные программного ГСЧ могут иметь лучшие статистические свойства и создаваться быстрее, чем физического [2].
Генераторы случайных и псевдослучайных чисел являются важным звеном в обеспечении информационной безопасности. Это «строительные блоки» криптографических алгоритмов и протоколов. Поскольку такие генераторы применяются во многих криптографических задачах, например, формирование случайных параметров и ключей систем шифрования, то требования, предъявляемые к ним, оказываются достаточно высокими. В частности, одним из критериев абсолютно произвольной двоичной последовательности, получаемой на выходе генератора, является невозможность её предсказания в отсутствие какой-либо информации о данных, подаваемых на вход генератора. Поэтому на практике статистическими тестами проводят проверку случайного характера бинарной последовательности, формируемой генератором случайных или псевдослучайных чисел. Что в свою очередь позволяет выявить генераторы, заранее удовлетворяющие требованиям конкретной криптографической задачи.
В основе тестов лежит понятие нулевой гипотезы. Нулевая гипотеза – это предположение, что между двумя фактами отсутствует какая-либо взаимосвязь. Существует также альтернативная гипотеза, которая опровергает нулевую гипотезу: т.е. между явлениями взаимосвязь существует. Если переходить к терминам случайных чисел, то за нулевую гипотезу принимается предположение, что последовательность является истинно случайной, знаки которой появляются равновероятно и независимо друг от друга. Следовательно, если нулевая гипотеза верна, то генератор производит достаточно «хорошие» случайные числа.
С одной стороны, имеется статистика, подсчитанная на основе фактически собранных данных, т. е. по измеряемой последовательности. С другой стороны, есть эталонная статистика, получаемая математическими методами (теоретически вычисленная), которую бы имела истинно случайная последовательность. Очевидно, что собранная статистика не может сравняться с эталонной – насколько бы не был хорошо генератор, он все равно не идеален. Поэтому вводят некую погрешность, например, 5%. Она означает, что если собранная статистика отклоняется от эталонной больше чем на 5%, то делается вывод о том, что нулевая гипотеза не верна с большой надежностью.
Существует 4 варианта развития событий:
· сделан вывод о том, что последовательность случайна, и это верный вывод;
· сделан вывод о том, что последовательность не случайна, хотя она была на самом деле случайна. Такие ошибки называют ошибками первого рода;
· последовательность признана случайной, хотя на самом деле таковой не является. Такие ошибки называют ошибками второго рода;
· последовательность справедливо отбракована [1].
Вероятность ошибки первого рода называют уровнем статистической значимости и обозначают как α. Т. е. α – это вероятность отбраковать «хорошую» случайную последовательность. Это значение определяется областью применения. В криптографии принято α брать от 0.001 до 0.01.
В каждом тесте вычисляется так называемое P-значение – это вероятность того, что подопытный генератор произведет последовательность не хуже, чем гипотетический истинный. Если Pзначение равно 1, то последовательность идеально случайна, а если оно равно 0, то последовательность полностью предсказуема.
Дальше P-значение сравнивается с α, и если оно больше α, то нулевая гипотеза принимается и последовательность признается случайной. В противном случае – отбраковывается. Обычно α выбирается между 0.001 и 0.01.
В тестах берется α = 0.01 [1]. Из этого следует, что:
если P-значение ≥ 0.01, то последовательность признается случайной с уровнем доверия 99%;
если P-значение < 0.01, то последовательность отбраковывается с уровнем доверия 99%.
Следующие предположения сделаны относительно случайных двоичных последовательностей, которые будут проверяться:
· однородность. В любой момент генерации последовательности случайных или псевдослучайных битов появление нуля или единицы одинаково вероятно, т. е. вероятность каждого равна точно 1/2. Ожидаемое количество нулей (или единиц) равно n / 2, где n – длина последовательности;
· масштабируемость. Любой тест, применимый к последовательности, также может применяться к подпоследовательностям, извлеченным случайным образом. Если последовательность является случайной, то любая такая извлеченная подпоследовательность также должна быть случайной. Следовательно, любая извлеченная подпоследовательность должна пройти любой тест на случайность;
· согласованность. Поведение генератора должно быть одинаковым для всех начальных значений (начальных значений). Недостаточно тестировать программный ГСЧ на основе выходных данных одного источника или физический ГСЧ на основе выходных данных одного физического выхода.
2.2. Методы корреляционного анализа
Автокорреляционная функция (АКФ) позволяет увидеть периодичность в ряде данных и представляет собой зависимость взаимосвязи между сигналом и ее сдвинутой копией от величины временного сдвига.
Для случайных процессов АКФ случайной функции X(t) имеет вид:
 , (2.1)
, (2.1)
где 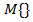 - математическое ожидание.
- математическое ожидание.
АКФ помогает находить повторяющиеся участки сигнала и используется в обработке сигналов.
В статистике автокорреляция случайного процесса описывает корреляцию между значениями процесса в различные моменты времени. График автокорреляций выборки в зависимости от сдвига называется коррелограммой.
Основным свойством АКФ является симметричность, т.е. R(i) = R(-i). В непрерывном случае автокорреляция это четная функция: R(- 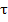 ) = R(
) = R( 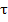 ).
).
2.2. Алгоритмы проверки последовательности случайных чисел
2.2.1 Частотный побитовый тест
Суть данного теста заключается в определении соотношения между нулями и единицами во всей двоичной последовательности. Тест оценивает, насколько близка доля единиц к 0,5. Если вычисленное в ходе теста значение вероятности P‑значение < 0,01, то данная двоичная последовательность не является истинно случайной. В противном случае, последовательность носит случайный характер.
Порядок действий.
1. Принимаем каждую «1» за +1, а каждый «0» за –1 и считаем сумму по всей последовательности:
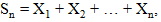
| (2.2) |
где 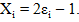
2. Вычисляем статистику:
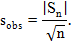
| (2.3) |
3. Вычисляем P-значение через дополнительную функцию ошибок:
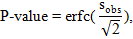
| (2.4) |
где erfc(x) – дополнительная функция ошибок, которая равна

| (2.5) |
Рекомендуется тестировать последовательности длиной не менее 100 бит [1].
2.2.2 Частотный блочный тест
Целью теста является обнаружение отклонений от идеальной 50% частоты единиц путем разложения тестовой последовательности на несколько непересекающихся подпоследовательностей и применения гипотезы 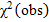 для однородного соответствия эмпирических частот идеальной 1/2. Строка из 0 и 1 (или эквивалентных -1 и 1) разбивается на несколько непересекающихся подстрок. Для каждой подстроки вычисляется доля единиц. Гипотеза
для однородного соответствия эмпирических частот идеальной 1/2. Строка из 0 и 1 (или эквивалентных -1 и 1) разбивается на несколько непересекающихся подстрок. Для каждой подстроки вычисляется доля единиц. Гипотеза 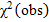 сравнивает эти пропорции подстроки с идеальной 1/2. Параметрами этого теста являются M и N, так что n = MN, т. е. исходная строка разбивается на N подстрок, каждая длиной M. Для каждой из этих подстрок вероятность их оценивается по наблюдаемой относительной частоте единиц, πi, i = 1,..., N.
сравнивает эти пропорции подстроки с идеальной 1/2. Параметрами этого теста являются M и N, так что n = MN, т. е. исходная строка разбивается на N подстрок, каждая длиной M. Для каждой из этих подстрок вероятность их оценивается по наблюдаемой относительной частоте единиц, πi, i = 1,..., N.
Порядок действий.
1. Разбиваем последовательность на блоки длиной M (биты, не сформировавшие полный блок, отсеиваются):
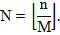
| (2.6) |
2. Подсчитываем пропорции единиц в каждом блоке:
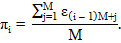
| (2.7) |
3. Вычисляем статистику:
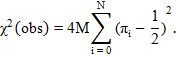
| (2.8) |
4. Вычисляем P-значение через неполную верхнюю гамма-функцию:
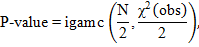
| (2.9) |
где Q(a, x) – неполная верхняя гамма-функция:

| (2.10) |
и Г(z) – стандартная гамма-функция:

| (2.11) |
Рекомендуется анализировать последовательности длиной не менее 100 бит, а также должны выполняться соотношения M ≥ 20, M > 0.01n и N < 100 [1].
2.2.3 Тест на одинаковые идущие подряд биты
В тесте ищутся все последовательности одинаковых битов, а затем анализируется, насколько количество и размеры этих последовательностей соответствуют количеству и размерам истинно случайной последовательности. Смысл в том, что если смена 0 на 1 (и обратно) происходит очень редко, то такая последовательность меньше похожа на случайную [1].
Порядок действий.
1. Вычисляем долю единиц в всей последовательности:
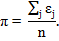
| (2.12) |
2. Проверяем, удовлетворяется ли условие 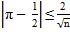 . Если условие не удовлетворяется, то тест завершается и считается неуспешным, а если удовлетворяется – тест продолжает выполняться.
. Если условие не удовлетворяется, то тест завершается и считается неуспешным, а если удовлетворяется – тест продолжает выполняться.
3. Вычисляем суммарное число знакоперемен:
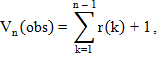
| (2.13) |
где 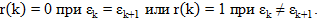
4. Вычисляем P-значение через дополнительную функцию ошибок (1.4):

| (2.14) |
2.2.4 Тест на самую длинную последовательность из единицы в блоке
Исходная последовательность из n битов разбивается на N блоков, каждый по M бит. После чего в каждом блоке ищется самая длинная последовательность единиц, а затем оценивается, насколько показатель близок к такому же показателю для истинно случайной последовательности. Аналогичного теста на нули не требуется, так как если единицы распределены хорошо, то нули также будут распределены хорошо [1].
NIST рекомендует несколько опорных значений, как разбивать на блоки, которые приведены в таблице 2.1.
Таблица 2.1 – Рекомендация NIST по разбиению последовательности на блоки
| Общая длина последовательности, N | Длина блока, M |
| 128 | 8 |
| 6272 | 128 |
| 75000 | 10000 |
Порядок действий.
1. Разбиваем последовательность на блоки длиной M и рассчитываем максимальную последовательность из подряд идущих единиц для каждого блока.
2. Рассчитываем частоты на основе таблицы 2.2. Например, если длина блока M равна 8, а в блоке максимальная последовательность из подряд идущих единиц равна 2, то к частоте 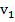 прибавляем 1. И так для каждого блока.
прибавляем 1. И так для каждого блока.
Таблица 2.2 – Частоты и условия их увеличения при различных длинах блока

| M = 8 | M = 128 | M = 104 |

| ≤ 1 | ≤ 4 | ≤ 10 |
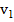
| 2 | 5 | 11 |
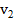
| 3 | 6 | 12 |
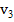
| ≥ 4 | 7 | 13 |
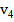
| – | 8 | 14 |
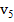
| – | ≥ 9 | 15 |
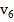
| – | – | ≥ 16 |
3. Рассчитываем гипотезу 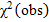 :
:
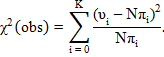
| (2.15) |
где K и N – константы, значения которых выбирается из таблицы 2.3;
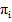 – теоретические константы, которые выбираются исходя из значений K и M, значение которых выбирается из таблицы 1.4 [1].
– теоретические константы, которые выбираются исходя из значений K и M, значение которых выбирается из таблицы 1.4 [1].
Таблица 2.3 – Значения K и N в зависимости от длины блока M
| M | K | N |
| 8 | 3 | 16 |
| 128 | 5 | 49 |
| 104 | 6 | 75 |
Таблица 2.4 – Значение теоретических констант 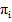
| Значение K и N | Частоты | Вероятности |
| K = 3, M = 8 | { 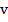 ≤ 1} ≤ 1}
| 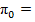 0.2148 0.2148
|
{ 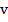 = 2} = 2}
|  0.3672 0.3672
| |
| {v = 3} | 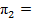 0.2305 0.2305
| |
| {v ≥ 4} |  0.1875 0.1875
| |
| K = 5, M = 128 | {v ≤ 4} | 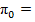 0.1174 0.1174
|
| {v = 5} |  0.2430 0.2430
| |
| {v = 6} | 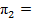 0.2493 0.2493
| |
| {v = 7} |  0.1752 0.1752
| |
| {v = 8} | 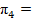 0.1027 0.1027
| |
| {v ≥ 9} |  0.1124 0.1124
| |
| K = 6, M = 10000 | {v ≤ 10} | 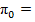 0.0882 0.0882
|
| {v = 11} |  0.2092 0.2092
| |
| {v = 12} | 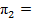 0.2483 0.2483
| |
| {v = 13} |  0.1933 0.1933
| |
| {v = 14} | 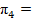 0.1208 0.1208
| |
| {v = 15} |  0.0675 0.0675
| |
| {v ≥ 16} | 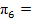 0.0727 0.0727
|
4. Вычисляем P-значение с помощью неполной верхней гамма-функцией:
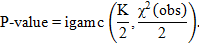
| (2.16) |
2.2.5 Тест рангов бинарных матриц
Этот тест анализирует матрицы, которые составлены из исходной последовательности, а именно – рассчитывает ранги непересекающихся подматриц, построенных из исходной двоичной последовательности. В основе теста лежат исследования случайных матриц, состоящих из 0 и 1. Показано, что можно спрогнозировать вероятности того, что матрица M x Q будем иметь ранг R, где R = 0, 1, 2, ... min(M, Q).
Порядок действий.
1. Последовательно разделить последовательность на непересекающиеся блоки длиной MQ. Количество блоков будет равно:

| (2.17) |
Биты, которые не вошли в блок, отбрасываются и не используются при расчетах. Каждый блок собирается в матрицу MxQ, которая собирается построчно символами последовательности.
2. Вычисляется ранг каждой матрицы.
3. FM равно количеству матриц с Rl = M, l = 1, …, N.
FM – 1 равно количеству матриц с Rl = M – 1.
N – FM – FM – 1 равно количеству остальных матриц.
4. Вычисляем гипотезу 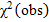 :
:
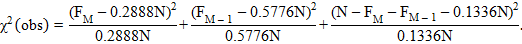
| (2.18) |
5. Вычисляем P-значение с помощью неполной верхней гамма-функцией:

| (2.19) |
NIST рекомендует, чтобы общая длина последовательности была не менее 38MQ [1].
2.2.6 Тест приблизительной энтропии
Согласно классическому определению, энтропия является мерой хаоса: чем она выше, тем более непредсказуемые явления. Для случайных последовательностей, используемых в криптографии, важно иметь высокую энтропию – это значит, что сложно предсказать последующие случайные биты на основе того, что уже имеется.
Тест вычисляет частоты появления всевозможных образцов заданной длины m, а затем аналогичные частоты, но уже для образцов длиной m + 1. Затем распределение частот сравнивается с эталонным распределением  . В этом тесте образцы могут перекрываться [1].
. В этом тесте образцы могут перекрываться [1].
Порядок действий.
1. Дополняется в конце последовательность первыми m – 1 битами.
2. Считаем встречаемость каждого из  всевозможных блоков. Например, если m = 2, то количество всевозможных блоков будет равно
всевозможных блоков. Например, если m = 2, то количество всевозможных блоков будет равно 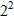 : 00, 01, 10, 11.
: 00, 01, 10, 11.
3. Посчитаем соответствующие частоты по формуле:
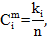
| (2.20) |
где 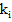 – количество i-того блока в последовательности.
– количество i-того блока в последовательности.
4. Вычисляем  :
:
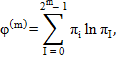
| (2.21) |
где  ;
;
 .
.
5. Повторить шаги 1 – 4, заменив m на (m + 1).
6. Рассчитываем  :
:
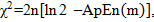
| (2.22) |
где  .
.
7. Вычисляем P-значение с помощью неполной верхней гамма-функцией:

| (2.23) |
2.2.7 Тест кумулятивных сумм
Тест заключается в максимальном отклонении от нуля при произвольном обходе, определяемым кумулятивной суммой заданных (–1, +1) цифр в последовательности. Цель данного теста – определить является ли кумулятивная сумма частичных последовательностей, возникающих во входной последовательности, слишком большой или слишком маленькой по сравнению с ожидаемым поведением такой суммы для абсолютно случайной входной последовательности. Данный тест имеет два режима: прямой – суммы считаются с первого элемента, обратный – с последнего [1].
Порядок действий.
1. Заменяем каждую «1» за +1, а каждый «0» за –1 и считаем сумму по всей последовательности:
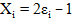
| (2.24) |
2. Вычисляем частичные суммы  с первого бита при прямом режиме или с последнего при обратном. Подробное описание суммы отображено в таблице 1.5.
с первого бита при прямом режиме или с последнего при обратном. Подробное описание суммы отображено в таблице 1.5.
Таблица 2.5 – Прямой и обратный режимы суммирования
| Прямая | Обратная |
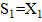

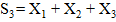 …
…
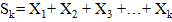 …
…

| 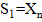

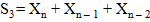 …
…
 …
…

|
| Sk = Sk–1 + Xk | Sk = Sk–1 + Xn – k + 1 |
3. Выбираем максимальное значение суммы:
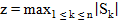
| (2.25) |
4. Рассчитываем P-значение:

| (2.26) |
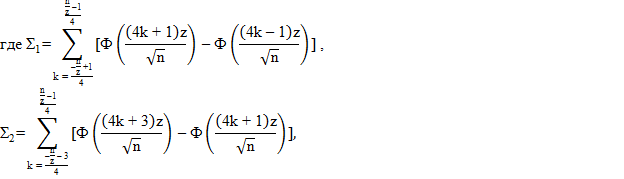
где Ф(z) – функция распределения нормальной случайной величины:
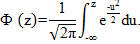
| (2.27) |
3 Приборы и оборудование
1. Персональный компьютер.
2. Цифровой осциллограф BORDO.
3. Квантовый генератор случайных числовых последовательностей.
4. Пакет прикладных программ MATLABR2015b (8.6.0) и RandomTest.
4 Порядок выполнения работы
1. Произвести внешний осмотр оборудования рабочего места и убедиться визуально в отсутствии каких-либо повреждений и дефектов.
2. Подключить ПГСЧ с помощью кабеля USBAM-BM к порту USB ПЭВМ. С помощью соединительного кабеля подключить выход генератора XS3 к входу цифрового осциллографа BORDO. Включить персональный компьютер и запустить цифровой осциллограф BORDO.
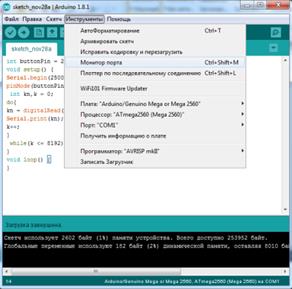
3. Запустить программу ARDUINO. В открывшемся окне « Sketch_ Arduino» в меню «Скетч» выбрать пункт «Загрузка» и загрузить скетч в память Arduino.
Скетч и результаты загрузки показаны на рисунке 2.1
 |
|
 |
Далее в меню «Инструменты» выбрать пункт «Монитор порта» (рисунок 2.2) и в открывшемся окне наблюдать числовую двоичную последовательность (рисунок 2.3)
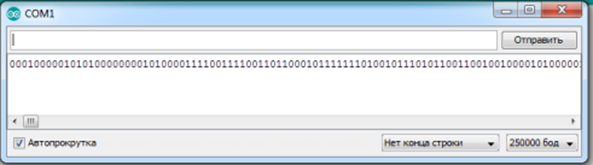 |
Рисунок 2.3 Случайная числовая двоичная последовательность
Примечание – Если порт COM1 недоступен, то необходимо в меню «Пуск» кликнуть правой кнопкой мыши по пункту «Компьютер», выбрать пункт «Свойства» и в открывшемся окне в левом верхнем углу выбрать пункт «Диспетчер устройств». В открывшемся окне «Диспетчер устройств» открыть порты « COM и LPT » двойным щелчком левой кнопкой мыши. Затем в подпункте « USB - SerialCH 340» кликнуть правой кнопкой мыши и выбрать пункт «Свойства». В открывшемся окне « USB - SerialCH 340» выбрать меню «Параметры порта» (рисунок 2.4).
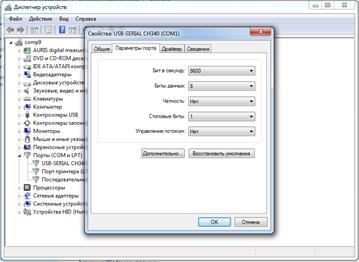 |
Рисунок 2.4 Параметры порта
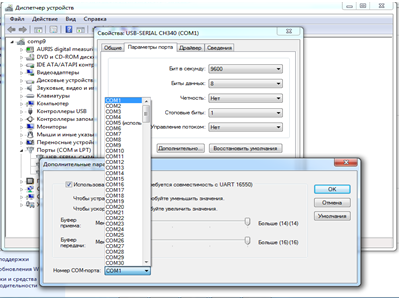 |
Затем нажать на кнопку «Дополнительно» и выбрать номер COM-порта (COM1) (рисунок 2.5), после чего нажать кнопку ОК.
Модуль ARDUINO на основе микроконтроллера ATmega 2560 преобразует двухуровневый случайный цифровой шумовой сигнал в последовательность 0 и 1, которая преобразуется в ПК в текстовый файл длиной 8К (длина задается программно).
4. Кликнуть левой клавишей мыши в свободном поле окна COM1. Выделить весь текстовый файл ( Ctrl + A ) и скопировать ( Ctrl + C ). Создать текстовый документ в новой папке, вставить в него скопированный текстовый файл ( Ctrl + V ) и сохранить.
Пример открытого текстового файла для двоичной числовой последовательности показан на рисунке 2.6.

Затем сохранённый текстовый файл обрабатывается в программе MATLAB для определения основных статистических и спектрально-временных параметров (автокорреляционная функция (АКФ), сбалансированность по 0 и 1, амплитудный и фазовый спектры), а также используется для получения ключей шифрования. Их случайность проверяется по стандартам NIST программой RANDOM_TEST.
5. Запустить программу MATLAB и с помощью пункта меню « HOME → Open » открыть листинг программы обработки случайной числовой последовательности « noise _ research _1. m ».
6. Запустить программу обработки случайной двоичной последовательности с помощью пункта меню « EDITOR → RUN ». Результаты обработки для цифрового случайного шумового сигнала (рисунок 3.3) представлены на рисунках 2.7, 2.8, 2.9.

Из рисунков 2.7, 2.8, 2.9 следует, что случайная двоичная последовательность сбалансирована по количеству нулей и единиц, имеет небольшой боковой выброс на АКФ при смещении 1907 и отличные амплитудный и фазовый спектры.

7. Запустить программу RANDOM TEST (рис.2.9). Форма интерфейса программы состоит из трех областей: «генерация ключа», «выбор тестов» и «результаты тестов». При запуске активной является только область «генерация ключа».
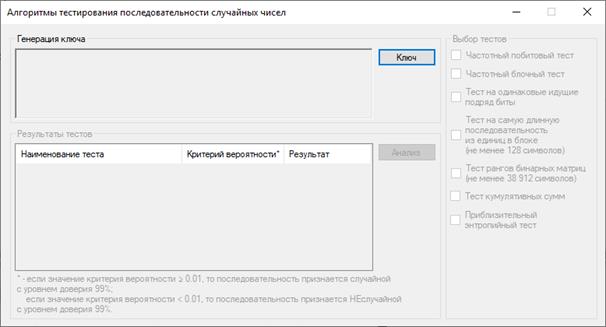
Рисунок 2.9 Форма интерфейса программы
 |
8. Загрузить случайную последовательность в программу. Для этого нужно нажать на кнопку «Ключ». Появляется диалоговое окно, в котором нужно выбрать файл с кодовой последовательностью (рисунок 2.10). По умолчанию выбран фильтр файлов с расширением «*.txt», но есть возможность отобразить все файлы. После выбора файла нужно нажать кнопку «Открыть», активными становятся остальные области, то есть доступен выбор тестов проверки алгоритмов, а в поле отображения ключа последовательность выводится ключ в коде base64 (рисунок 2.11).


9. Проверить на «случайность» последовательность случайных чисел с помощью следующих алгоритмов:
частотный побитовый тест;
частотный блочный тест;
тест на одинаковые идущие подряд биты;
тест на самую длинную последовательность из единиц в блоке (не менее 128 символов);
тест рангов бинарных матриц (не менее 38 912 символов);
тест кумулятивных сумм;
приблизительный энтропийный тест.
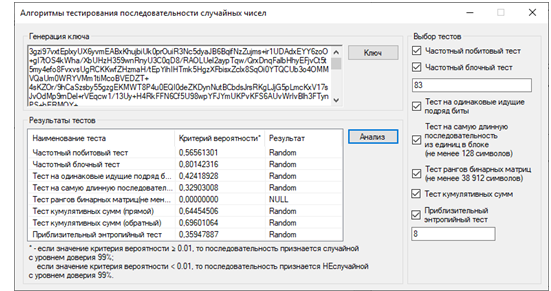 |
Дальше необходимо выбрать тесты, ввести дополнительные значения (если требуется) и нажать кнопку «Анализ». В табличном виде будет выведен результаты тестирования (рисунок 2.12).
Если требуется выбрать другой файл с последовательностью, то нужно нажать кнопку «Ключ» и проделать указанные ранее шаги. Чтобы закрыть программу достаточно в правом верхнем углу формы нажать на «×».
10. Провести контроль случайности последовательностей при других значениях напряжения, подаваемых на SiФЭУ.
11. Сделать краткие выводы по результатам работы.
12. Ответить на контрольные вопросы.
13. Оформить отчет и сдать зачет.
5 Контрольные вопросы
1. Назовите типы генераторов случайных чисел, их преимущества и недостатки.
2. Поясните принципы тестирования последовательностей случайных чисел.
3. Поясните алгоритмы, используемые в лабораторной работе для тестирования последовательностей случайных чисел.
ЛИТЕРАТУРА
1. A Statistical Test Suitefor Random and Pseudorandom Number Generators for Cryptographic Applications / National Institute of Standards and Technology. – Gaithersburg, Maryland, 2010.
2. Основы современной криптографии : учебный курс. / С. Г. Баричев, В. В. Гончаров, Р. Е. Серов – 2-е изд., испр. и доп. – М. : Горячая линия – Телеком, 2002. – 175 с.
3. Дроздова, И. И. Генераторы случайных и псевдослучайных чисел / И. И. Дроздова, В. В. Жилин // Технические науки в России и за рубежом : материалы VII Междунар. науч. конф. : сб. науч. тр. : в 2 ч. / отв. Ред. И. Г. Ахметов. – М. : Буки-Веди, 2017. – С. 13-16.
|
из
5.00
|
Обсуждение в статье: ЛАБОРАТОРНАЯ РАБОТА № 2. ИЗУЧЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ СЛУЧАЙНЫХ ЧИСЕЛ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

