 |
Главная |
Математический аппарат.
|
из
5.00
|
ОПТИМИЗАЦИЯ ПРОФИЛЯ ОТРАЖЕНИЯ ЧАСТОТНЫХ ФИЛЬТРОВ ИЗЛУЧЕНИЯ С ИСПОЛЬЗОВАНИЕМ МОДУЛИРОВАННЫХ СВЕРХРЕШЕТОК
Содержание. 
1. Введение. 3
2. Математический аппарат. 6
3. Немодулированные бинарные структуры. 11
4. Модулированные бинарные структуры. 16
4.1 . Ступенчато модулированные решетки. 16
4.2 . Решетки со стековой модуляцией. 21
4.3 . Бинарные решетки с гауссовыми модуляциями. 25
5. Заключение. 35
6. Приложение. 38
7. Список использованной литературы. 42
Введение.
Бинарные периодические структуры, как известно, обладают как частотными зонами с предельно малым пропусканием, так и зонами с малым отражением. Данное свойство служат основой для использования таких сред в качестве, например, селективных частотных фильтров, или управляемых зеркал. Свойство это основано на многолучевой интерференции, дающей минимумы в одних частотных диапазонах и максимумы в других. Некоторые из этих зон (пропускания или отражения) являются «хорошими»: то есть гладкими и с вертикальными краями. Некоторые же являются сильно возмущенными, что затрудняет их использование для управления излучением.
В работе главным ограничением являются показатели преломления. Было предложено использовать вещества с показателями преломления 1.44 и 2.0 или 1.44 и 2.2, из-за того, что остальные вещества являются либо нетехнологичными и, соответственно, представляют собой чисто теоретический интерес, либо нестойкими к лазерному излучению, что приводит к их скорому разрушению. Следующим ограничением является частотный диапазон. Рабочая частота, то есть минимумы и максимумы отражения должны лежать в видимом диапазоне, что соответствует циклической частоте 1.5 * 1015 – 3.5 * 1015 Гц. Так как показатели преломления являются величинами жестко зафиксированными, то при модуляции предложено изменять толщины слоев, модулируя, таким образом, оптический путь.
В [1] было предложено использовать модулированный потенциальный барьер для получения гладких зон пропускания и отражения для электронных волн. В [2] была применена та же идея для сглаживания функции пропускания в соответствующих зонах оптического излучения. Более общая физическая теория подробно описана в [5] и, более применительно к данной теме, в [6]. Математическое обоснование всего проекта (как для расчетов, так и для написания программы) детально разработано в [3] и, применительно к данному случаю, в [4]. Наиболее же полная математическая идея общно и подробно изложена в [7].
В данном проекте рассматривается профиль отражения на частоте лазерного излучения. Было предложено три вида модуляции. Это «ступени» - скачкообразное изменение оптического пути с постепенным общим повышением или понижением значений. «Стеки» - набор из нескольких квазигармонических периодов изменения значений. И, наконец, «гауссианы» - здесь происходит изменение оптического пути по функции Гаусса - exp(-x2/s2), где параметр s - ширина всей структуры. При этом рассматривается модуляция для разного числа слоев в структуре.
Так же обсуждаются дальнейшие перспективы той или иной оптимизации, как то – возможности расширения зон отражения, получение более вертикальных и менее возмущенных краев этих зон, получение максимально возможного отражения или пропускания излучения, что, в свою очередь, означает обсуждение перспектив получения реально действующих поляризационных затворов, оптических фильтров и управляемых зеркал.
Следует оговорить обозначения принятые в этой работе. На графиках зависимостей отражения волны от частоты (они же называются профилями отражения) по оси абсцисс откладывается циклическая частота падающего излучения, а по оси ординат показатель отражения (отношение интенсивности отраженной волны к интенсивности падающей). А на графиках-изображениях оптического пути по оси абсцисс откладываются номера слоев, а по оси ординат соответствующие им произведения толщин на показатели преломления слоев. На самом деле это не вполне графики, в том смысле, что реально это набор дискретных точек. Трудно, ведь, представить себе слой под номером 2.4, например. Линии же существуют для очевидности этих точек и общей модуляции структуры. В местах с наиболее интересными (с точки зрения автора) результатами будут приводиться также и графики-схемы самих структур. Там по оси абсцисс отложены номера слоев, а по оси ординат толщины этих слоев. Замечания, относящиеся к графикам-изображениям оптического пути, остаются в силе и для этих графиков-схем.
Во всей работе показатели преломления слоев имеют значения 1.44 и 2.2. Это связано с тем, что наилучший результат получается при большой разбежке в показателях преломления ([2] – там использованы значения 1.44 и 3.48). Но такие вещества не стойки к излучению. Были проведены вычисления для показателей преломления 1.44 и 2.0, но результаты оказывались всегда чуть хуже.
Математический аппарат.
Современная оптика базируется на уравнениях Максвелла
Ñ х E = - 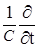 B Ñ B = 0
B Ñ B = 0
(1) Ñ х H =  j +
j + 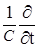 D Ñ D = 4pr ,
D Ñ D = 4pr ,
где векторы E и D характеризуют электрическое поле, а B и H - магнитное, r - объемная плотность электрического заряда, j – плотность электрического тока. Максвелл также дополнил систему (1) системой материальных уравнений, отражающей свойства среды, в которой находятся заряды и токи:
D = 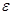 E , B = mH , j = s E , (2)
E , B = mH , j = s E , (2)
где 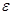 - диэлектрическая проницаемость, m - магнитная проницаемость, s - удельная электропроводность среды.
- диэлектрическая проницаемость, m - магнитная проницаемость, s - удельная электропроводность среды.
При падении плоской монохроматической волны
Н(r, t) = H0ei(kmr - wt), k = w/c (3)
на границу раздела однородных анизотропных сред возникают отраженные и преломленные волны с одинаковой экспоненциальной зависимостью exp (ikbr) от тангенциальной составляющей rt радиус-вектора r [8], где b = Im – тангенциальная составляющая вектора рефракции m падающей волны (br = brt).
Зависимость векторов поля в среде от нормальной компоненты
z = qr вектора r в общем случае не является экспоненциальной. В анизотропных средах отраженные волны могут иметь различные нормальные составляющие векторов рефракции.
В рассматриваемом случае поле отраженной волны в анизотропной среде описывается [3] функциями вида:
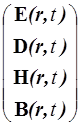 =
= 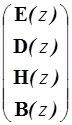 ei(kbr - wt) (4)
ei(kbr - wt) (4)
Аналогичной [3] зависимостью от координат характеризуются поля, возбуждаемые волной (3) в системах однородных плоскопараллельных слоев.
Для таких полей ротор сводится к оператору qx 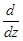 + ikbx и уравнения Максвелла (1) принимают вид
+ ikbx и уравнения Максвелла (1) принимают вид
(qx 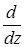 + ikbx)H = -ikD (5)
+ ikbx)H = -ikD (5)
(qx 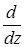 + ikbx)E = ikB
+ ikbx)E = ikB
Умножая уравнения (5) на вектор q, получаем соотношения
qD = aH , qB = -aE , a = b  q (6)
q (6)
При нормальном падении (b = 0) поле (4) представляет собой плоскую волну. Нормальные компоненты векторов электрической и магнитной индукции такой волны равны нулю: qD = qB = 0. Векторы электромагнитного поля в линейной среде связаны уравнениями
D = 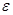 E , B = mH , (7)
E , B = mH , (7)
где 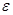 и m - тензоры диэлектрической и магнитной проницаемостей. В общем случае поглощающей анизотропной среды, обладающей собственной или вынужденной гиротропией [9],
и m - тензоры диэлектрической и магнитной проницаемостей. В общем случае поглощающей анизотропной среды, обладающей собственной или вынужденной гиротропией [9], 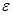 и m - комплексные несимметричные тензоры.
и m - комплексные несимметричные тензоры.
Уравнения связи (7) и соотношения (6) образуют систему восьми линейных скалярных уравнений для двенадцати декартовых компонент векторных функций E(z), D(z), H(z), B(z) вида (4). Поэтому лишь четыре из этих компонент линейно независимы. В качестве независимых функций удобно выбрать тангенциальные компоненты векторов напряженности электрического и магнитного полей, так как они непрерывны на границе раздела слоев. Выражая из уравнений (6) и (7) нормальные компоненты через тангенциальные составляющие и используя тождество [3] H = Ht +q  qH , получаем
qH , получаем
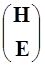 = V
= V 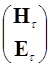 , где (8)
, где (8)
V = 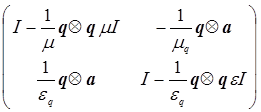 - (9)
- (9)
матрица восстановления [10] полных векторов H и E по их тангенциальным составляющим Ht и Et , а 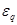 = q
= q 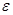 q,
q, 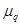 = q
= q  q.
q.
С учетом соотношения (8) систему уравнений (5) можно представить в матричном виде [11]
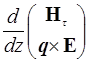 = ikM
= ikM 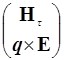 , (10)
, (10)
где
М = 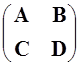 (11)
(11)
- блочная матрица, составленная из операторов (12)
A = 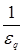 qx
qx 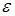 qa -
qa - 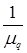 bq
bq 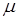 I
I
B = 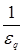 I
I 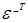 I -
I - 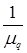 b
b 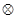 b (12)
b (12)
C = - 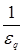 a
a 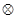 a -
a - 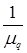 qx
qx 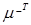 qx
qx
D = - 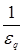 aq
aq 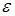 qx -
qx - 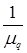 I
I 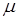 qb
qb
здесь 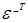 и
и 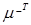 - тензоры, взаимные к транспонированным тензорам
- тензоры, взаимные к транспонированным тензорам
 и
и 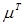 соответственно.
соответственно.
В прозрачных средах 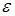 и
и 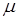 - эрмитовы:
- эрмитовы: 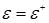 ,
, 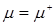 при вещественном параметре b имеют место равенства
при вещественном параметре b имеют место равенства
B+ = B, C+ = C, D+ = A (13)
В координатной записи уравнение (10) представляет собой систему четырех линейных дифференциальных уравнений для тангенциальных составляющих векторов H и E. Подобная система рассматривалась в [12].
Общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами выражается через экспоненциал от матрицы коэффициентов этой системы.
В нашем случае [7] имеет место
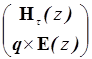 = P
= P 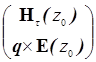 , P =
, P = 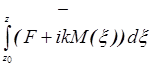 , F=
, F= 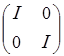 (14)
(14)
Р – характеристическая матрица плоскослоистой анизотропной системы, которая связывает значения полей на первой и последней границах системы. Для системы из N-1 слоев матрицу Р можно представить в виде
Р = РN-1PN-2…PP…P1, где РР = 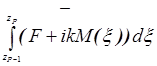 , р = 1, 2, …,N-1 – характеристическая матрица р-го слоя.
, р = 1, 2, …,N-1 – характеристическая матрица р-го слоя.
Если в пределах некоторого слоя значения функции М( 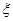 ) в двух произвольных точках
) в двух произвольных точках 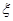 1 и
1 и 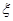 2 коммутируют между собой, то есть
2 коммутируют между собой, то есть
М( 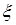 1) М(
1) М( 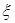 2) = М(
2) = М( 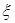 2)М(
2)М( 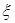 1) ,
1) , 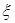 1,2 Î [zP-1, zP], то матрица Р этого слоя принимает вид [7] P = exp (ik
1,2 Î [zP-1, zP], то матрица Р этого слоя принимает вид [7] P = exp (ik 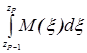 ). Для однородной среды соответствующий интеграл сводится [4] к экспоненциальному оператору
). Для однородной среды соответствующий интеграл сводится [4] к экспоненциальному оператору
Р = exp (iklM), где l – толщина слоя.
А такое уравнение легко алгоритмизуется. Ниже будет приведен листинг программы с комментариями.
|
из
5.00
|
Обсуждение в статье: Математический аппарат. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

