 |
Главная |
Исследование теоретико-игровой модели
|
из
5.00
|
Докажем существование доминирующей стратегии в антагонистической игре  , описанной в предыдущем параграфе.
, описанной в предыдущем параграфе.
С этой целью с учетом условий (3.1.12) и (3.1.13) запишем формулу (3.1.10) в следующем виде:
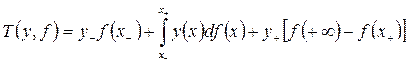 ,
,
где 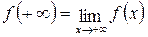 .
.
Теперь рассмотрим “усеченную” антагонистическую игру 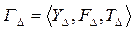 , в которой множество стратегий 1-го (2-го) игрока совпадает с множеством
, в которой множество стратегий 1-го (2-го) игрока совпадает с множеством  всех функций, каждая их которых представляет собой сужение на промежуток
всех функций, каждая их которых представляет собой сужение на промежуток 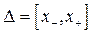 той или иной функции
той или иной функции 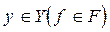 , а функция выигрыша
, а функция выигрыша 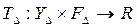 имеет вид
имеет вид
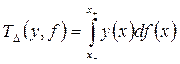 ,
, 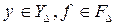 .
.
Из определения игр 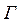 и
и 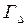 следует, что если будет доказано существование доминирующей стратегии 1-го игрока
следует, что если будет доказано существование доминирующей стратегии 1-го игрока 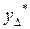 в игре
в игре 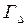 , то стратегия
, то стратегия 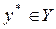 такая, что
такая, что
 (3.2.1)
(3.2.1)
будет доминирующей стратегией 1-го игрока в игре 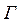 . Эту стратегию
. Эту стратегию 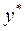 естественно считать оптимальной модельной шкалой средних ставок налога при заданных параметрах
естественно считать оптимальной модельной шкалой средних ставок налога при заданных параметрах  ,
,  ,
, 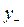 ,
, 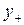 ,
, 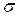 ,
, 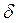 .
.
Для доказательства существования доминирующей стратегии 1-го игрока в игре 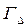 зафиксируем произвольную стратегию 2-го игрока
зафиксируем произвольную стратегию 2-го игрока 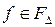 и рассмотрим задачу на максимум функционала
и рассмотрим задачу на максимум функционала
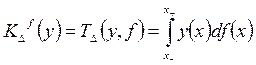 , (3.2.2)
, (3.2.2)
где 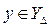 .
.
Очевидно, что если будет доказано, что задача имеет решение, не зависящее от выбранной функции 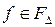 , то это решение будет доминирующей стратегией 1-го игрока в игре
, то это решение будет доминирующей стратегией 1-го игрока в игре 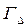 . Докажем это сначала в том случае, когда
. Докажем это сначала в том случае, когда 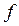 дифференцируема и имеет при почти всех
дифференцируема и имеет при почти всех  положительную производную
положительную производную  . В этом случае интеграл Стилтьеса сводится к обычному интегралу Римана:
. В этом случае интеграл Стилтьеса сводится к обычному интегралу Римана:
 .
.
Следовательно, задача на максимум функционала (3.2.2) сводится к следующей задаче оптимального управления:
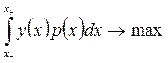 , (3.2.3)
, (3.2.3)
 (3.2.4)
(3.2.4)

 ,
,
 , (3.2.5)
, (3.2.5)
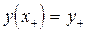 (3.2.6)
(3.2.6)
 .
.
Найдем решение уравнения (3.2.4), соответствующее произвольному допустимому управлению 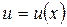 с начальным условием (3.2.5), которое имеет вид [19]
с начальным условием (3.2.5), которое имеет вид [19]
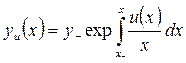 . (3.2.7)
. (3.2.7)
По этой формуле найдем решения уравнения (3.2.4) с начальным условием (3.2.5), соответствующие двум постоянным управлениям 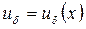 ,
,  и
и 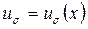 ,
, 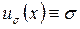 . Нетрудно видеть, что эти решения имеют вид
. Нетрудно видеть, что эти решения имеют вид
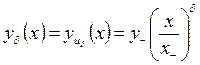 , (3.2.8)
, (3.2.8)
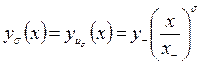 . (3.2.9)
. (3.2.9)
Так как предполагается, что 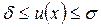 при почти всех
при почти всех 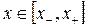 , то для решений (3.2.7) – (3.2.9) будет справедливым неравенство
, то для решений (3.2.7) – (3.2.9) будет справедливым неравенство
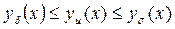 .
.
При 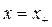 , с учетом формул (3.2.8) и (3.2.9), запишем полученное неравенство в виде
, с учетом формул (3.2.8) и (3.2.9), запишем полученное неравенство в виде
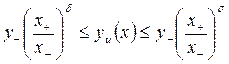
Поэтому если здесь управление 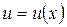 является допустимым в задаче (3.2.3) – (3.2.6), т.е. если
является допустимым в задаче (3.2.3) – (3.2.6), т.е. если  , то должны выполняться неравенства
, то должны выполняться неравенства
 . (3.2.10)
. (3.2.10)
Докажем теперь обратное, т. е. если справедливо неравенство (3.2.10), то в задаче (3.2.3) – (3.2.6) существует допустимое управление. Для этого запишем неравенство (3.2.10) с учетом формул (3.2.8) и (3.2.9) в виде
 .
.
С учетом определения решений  и
и  , а также с учетом теоремы о непрерывной зависимости решений дифференциального уравнения от параметров [19], это означает, что в задаче (3.2.3) – (3.2.6) существует, и при этом постоянное, допустимое управление
, а также с учетом теоремы о непрерывной зависимости решений дифференциального уравнения от параметров [19], это означает, что в задаче (3.2.3) – (3.2.6) существует, и при этом постоянное, допустимое управление 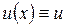 ,
, 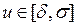 . Таким образом, справедливо следующее утверждение.
. Таким образом, справедливо следующее утверждение.
Лемма 3.2.1. Для того чтобы в задаче (3.2.3) – (3.2.6) существовало допустимое управление, а следовательно, множество стратегий 1-го игрока 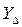 в игре
в игре 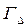 было непусто, необходимо и достаточно, чтобы выполнялись неравенства (3.2.10).
было непусто, необходимо и достаточно, чтобы выполнялись неравенства (3.2.10).
Далее нас будет интересовать случай, когда оба неравенства (3.2.10) выполняются как строгие. В противном случае, если одно из них выполняется как равенство, то, как следует из вывода этих неравенств, единственным допустимым управлением будет постоянное управление  (если как равенство выполняется левое из неравенств (3.2.10)), или же
(если как равенство выполняется левое из неравенств (3.2.10)), или же 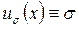 (если как равенство выполняется правое из неравенств (3.2.10)).
(если как равенство выполняется правое из неравенств (3.2.10)).
Функция Гамильтона в задаче (3.2.3.) – (3.2.6) имеет вид
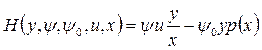 ,
,
поэтому сопряженное уравнение, в свою очередь, выглядит следующим образом:
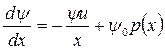 . (3.2.11)
. (3.2.11)
В соответствии с принципом максимума Понтрягина [32] можно утверждать, что для оптимального управления 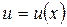 найдется такая постоянная
найдется такая постоянная  и такое нетривиальное решение
и такое нетривиальное решение 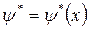 сопряженного уравнения, что для них и для решения
сопряженного уравнения, что для них и для решения 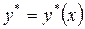 дифференциального уравнения (3.2.4), соответствующего оптимальному управлению
дифференциального уравнения (3.2.4), соответствующего оптимальному управлению 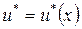 , при почти всех
, при почти всех 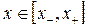 справедливо равенство
справедливо равенство
 ,
,
которое в рассматриваемой задаче принимает вид
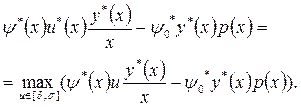
Нетрудно убедиться, что оптимальное управление имеет вид:

Для уточнения вида оптимального управления запишем решение сопряженного уравнения (3.2.11) по формуле Коши для линейного неоднородного уравнения 1-го порядка [19]:
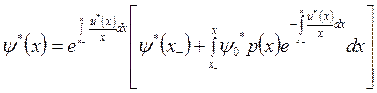 .
.
Функция  не является знакопостоянной и тождественно не равна нулю на интервале
не является знакопостоянной и тождественно не равна нулю на интервале 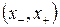 . Этими же свойствами обладает и функция
. Этими же свойствами обладает и функция 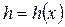 , где
, где 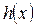 – выражение, стоящее в квадратных скобках правой части решения сопряженного уравнения. Поэтому
– выражение, стоящее в квадратных скобках правой части решения сопряженного уравнения. Поэтому  , в противном случае
, в противном случае 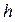 была бы тождественно равна постоянной
была бы тождественно равна постоянной 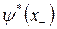 и, следовательно, была бы знакопостоянной. С учетом того, что
и, следовательно, была бы знакопостоянной. С учетом того, что 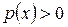 при почти всех
при почти всех 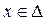 , можно утверждать, что функция
, можно утверждать, что функция 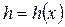 убывающая, кроме того, она не является знакопостоянной, в силу чего
убывающая, кроме того, она не является знакопостоянной, в силу чего 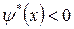 при
при 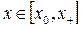 , а
, а 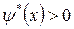 при
при 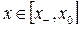 . Поэтому можно уточнить вид оптимального управления следующим образом:
. Поэтому можно уточнить вид оптимального управления следующим образом:
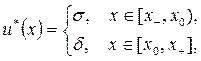 (3.2.12)
(3.2.12)
где точка переключения  определяется по формуле
определяется по формуле
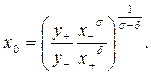 (3.2.13)
(3.2.13)
Решение краевой задачи (3.2.4) – (3.2.6), соответствующее найденному управлению 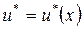 , имеет вид
, имеет вид
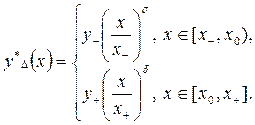 (3.2.14)
(3.2.14)
Учитывая связь между задачей (3.2.3) – (3.2.6) и задачей на максимум функционала (3.2.2) при ограничениях (3.2.4) – (3.2.6), получим следующее утверждение.
Лемма 3.2.2.Если оба неравенства (3.2.10) выполняются как строгие, то решение задачи на максимум функционала (3.2.2) при ограничениях (3.2.4) – (3.2.6) имеет вид (3.2.14), где точка  находится по формуле (3.2.13).
находится по формуле (3.2.13).
Возвращаясь к теоретико-игровой модели, докажем, что функция 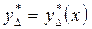 , значения которой находятся по формулам (3.2.14), (3.2.13), является доминирующей стратегией 1-го игрока в игре
, значения которой находятся по формулам (3.2.14), (3.2.13), является доминирующей стратегией 1-го игрока в игре 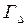 . Ранее (лемма 3.2.1) это было доказано при дополнительном предположении, что рассматриваемые функции
. Ранее (лемма 3.2.1) это было доказано при дополнительном предположении, что рассматриваемые функции 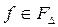 при почти всех
при почти всех 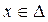 имеют положительную производную
имеют положительную производную 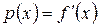 . Откажемся теперь от этого предположения. Выберем произвольные функции
. Откажемся теперь от этого предположения. Выберем произвольные функции 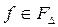 ,
, 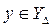 и покажем, что для них справедливо неравенство
и покажем, что для них справедливо неравенство
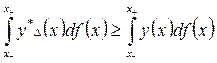 . (3.2.15)
. (3.2.15)
Из определения множества 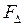 следует, что всякая функция
следует, что всякая функция 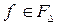 является неубывающей на интервале
является неубывающей на интервале 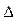 , поэтому неравенство (3.2.15) будет выполняться в том случае, если
, поэтому неравенство (3.2.15) будет выполняться в том случае, если
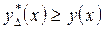 ,
, 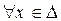 .
.
Причем решение 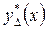 соответствует оптимальному управлению
соответствует оптимальному управлению 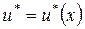 , а
, а 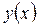 – некоторому допустимому управлению
– некоторому допустимому управлению 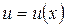 . По формуле (3.2.7) и с учетом краевого условия (3.2.5) эти решения можно представить в виде
. По формуле (3.2.7) и с учетом краевого условия (3.2.5) эти решения можно представить в виде
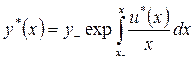 , (3.2.16)
, (3.2.16)
 . (3.2.17)
. (3.2.17)
Так как 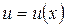 является допустимым управлением в задаче оптимального управления (3.2.3) – (3.2.6), то выполняется неравенство
является допустимым управлением в задаче оптимального управления (3.2.3) – (3.2.6), то выполняется неравенство
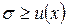 при почти всех
при почти всех 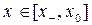 .
.
Как следует из (3.2.12), оптимальное управление на этом промежутке постоянно
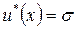 ,
, 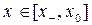 .
.
Тогда из формул (3.2.16), (3.2.17) и с учетом условия 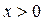 очевидно
очевидно
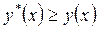 ,
, 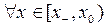 .
.
Рассмотрим, выполняется ли это неравенство на промежутке 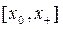 . Для доказательства этого неравенства заметим, что функции
. Для доказательства этого неравенства заметим, что функции  и
и 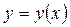 как решение краевой задачи (3.2.4) – (3.2.6) можно также представить в виде
как решение краевой задачи (3.2.4) – (3.2.6) можно также представить в виде
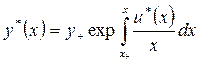 ,
, 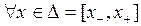 , (3.2.18)
, (3.2.18)
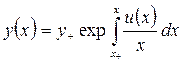 ,
, 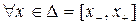 . (3.2.19)
. (3.2.19)
Опять воспользуемся тем, что 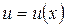 является допустимым управлением в задаче (3.2.3) – (3.2.6), и поэтому выполняется неравенство
является допустимым управлением в задаче (3.2.3) – (3.2.6), и поэтому выполняется неравенство
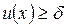 при почти всех
при почти всех 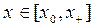 .
.
Откуда и из явного вида оптимального управления (3.2.12) имеем
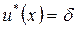 ,
, 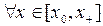 .
.
Следовательно, из формул (3.2.18) и (3.2.19) с учетом того, что в них 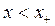 (
( 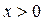 ), получим неравенство
), получим неравенство
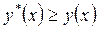 ,
, 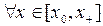 ,
,
что и требовалось доказать.
Возвращаясь к исходной задаче построения шкалы ставок налога, напомним, что из определения игр 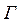 и
и 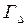 , с учетом формулы (3.2.1), можно записать вид оптимальной модельной шкалы. Таким образом, в результате проведенного анализа доказана следующая теорема.
, с учетом формулы (3.2.1), можно записать вид оптимальной модельной шкалы. Таким образом, в результате проведенного анализа доказана следующая теорема.
Теорема.1. Множество стратегий 1-го игрока 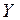 в игре
в игре 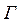 непусто тогда и только тогда, когда выполняются неравенства (3.2.10).
непусто тогда и только тогда, когда выполняются неравенства (3.2.10).
2. Если оба неравенства выполняются как строгие, то доминирующей стратегией 1-го игрока в игре 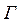 является функция
является функция
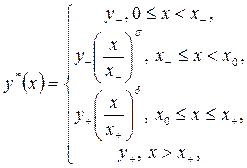 (3.2.20)
(3.2.20)
где точка переключения  вычисляется по формуле
вычисляется по формуле
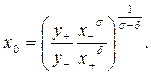 (3.2.21)
(3.2.21)
Следствие.Если одно из неравенств (3.2.10) выполняется как равенство, то множество стратегий 1-го игрока 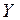 в игре
в игре 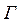 содержит только одну стратегию, которая, очевидно, является доминирующей стратегией 1-го игрока. Если как равенство выполняется левое из неравенств (3.2.10), то этой стратегией является функция
содержит только одну стратегию, которая, очевидно, является доминирующей стратегией 1-го игрока. Если как равенство выполняется левое из неравенств (3.2.10), то этой стратегией является функция
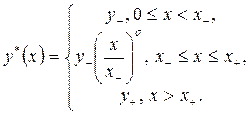
Если же как равенство выполняется правое из неравенств (3.2.10), то этой стратегией является функция
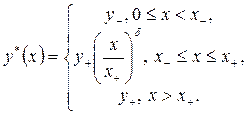
Таким образом, доказанная теорема позволяет считать полученную функцию  оптимальной (модельной) регрессивной шкалой средних ставок ЕСН. Эта функция определяется шестью экзогенными параметрами модели:
оптимальной (модельной) регрессивной шкалой средних ставок ЕСН. Эта функция определяется шестью экзогенными параметрами модели:  ,
,  ,
, 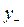 ,
, 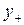 ,
, 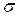 ,
, 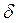 .
.
Для выбора этих параметров можно дать рекомендации, аналогичные тем, которые были рассмотрены в § 2.1.
Так же, как и при построении прогрессивной налоговой шкалы, практическое использование полученной регрессивной шкалы средних ставок ЕСН (3.2.20) – (3.2.1) затруднено тем, что она не может быть представлена в форме таблицы (шкалы предельных ставок налога). В соответствии с подходом, описанным в § 2.2 предыдущей главы, одним из возможных способов построения таблицы регрессивной шкалы предельных ставок ЕСН является решение задачи о наилучшем приближении оптимальной налоговой шкалы (3.2.20) – (3.2.1) такими шкалами средних ставок налога, которые допускают привычное табличное представление. Перейдем к описанию данной задачи, которое было представлено нами в [41].
|
из
5.00
|
Обсуждение в статье: Исследование теоретико-игровой модели |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

