 |
Главная |
Теорема Кантора о существовании множеств мощности более континуума
|
из
5.00
|
Пусть M - некоторое множество и P (M) - булеан множества M. Тогда |P(M)|>|M|.
Доказательство
Если множество M - конечно и |M|=n, то теорема верна, т.к. |P(M)|=  >n.
>n.
Очевидно, что для бесконечного множества M выполняется |P(M)|  |M|, так как множество P(M) содержит по крайней мере все одноэлементные подмножества из элементов множества M.
|M|, так как множество P(M) содержит по крайней мере все одноэлементные подмножества из элементов множества M.
Покажем что |P(M)|  |M|. Доказательство будем проводить от противного.
|M|. Доказательство будем проводить от противного.
Пусть |M|=|P(M)|, т.е. множества M и P(M) эквивалентны, а это означает, что между элементами этих множеств можно установить взаимно однозначное соответствие. Установим такое соответствие:
Элементу a из множества M поставим во взаимно однозначное соответствие множество A - элементы булеана P(M);
элементу в поставим во взаимно однозначное соответствие множество В (элемент множества (M));
элементус - множество С и т.д.
Постоим следующее множество X элементов из M:
для пары соответствующих членов (а,А) элемент амы поместим в множество Xтогда и только тогда, если элемент а не принадлежит множеству А, иэлементамы не поместим в множество X , если апринадлежит множествуА;алогично, элемент впомещаем в множество X , если этот элемент не принадлежит множеству В и не помещаем в множество X , если этот элемент принадлежит множеству В; так по всем элементам множества A.
Так как множество Xбудет состоять из элементов множества M, то это множество является элементом булеана множества M и ему, как и любому другому элементу из множества P(M), должен взаимно однозначно соответствовать некоторый элемент x из множества M.
Покажем, что этого не может быть.
Действительно, если элементxпринадлежит соответствующему ему множеству X, то этот элемент мы в множество Xвключить не должны, если же элемент xне принадлежит множеству X,то мы должны этот элемент включить в множество X.Полученное противоречие доказывает теорему.
Теорема Кантора-Бернштейна.
Пусть А и В произвольные множества. Если в в множестве А есть подмножество  эквивалентное множеству В, а в множестве В есть подмножество
эквивалентное множеству В, а в множестве В есть подмножество 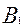 эквивалентное множеству А, то А и В эквивалентные множества.
эквивалентное множеству А, то А и В эквивалентные множества.
Доказательство.
Не уменьшая общности будем считать, что 
 А и
А и 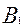
 В, так как если
В, так как если  =А или
=А или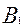 =В, то теорема верна.
=В, то теорема верна.
Так как  ~В, а
~В, а 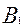
 B, то найдется множество
B, то найдется множество 

 , такое, что
, такое, что 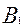 ~
~ .
.
Так как 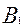 ~A, а
~A, а 
 A, то найдется множество
A, то найдется множество
 ~
~ . Получили, что А~
. Получили, что А~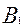 ~
~ , B~
, B~ ~
~ .
.
Продолжая аналогичные рассуждения, получим:
 ~
~  ,
,  ~
~ 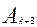 ,при этом
,при этом 

 ,k=1,2,... .
,k=1,2,... .
Отсюда следует, что
 \
\  ~
~  \
\ 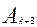 .(1)
.(1)
Обозначим черезD =A 





 ... .
... .
Тогда
A = D  (A\
(A\ )
)  (
(  \
\  )
)  (
(  \
\  )
)  (
(  \
\  )
)  ...=
...=
= D  (A\
(A\ )
)  (
(  \
\  )
)  (
(  \
\ 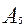 )...
)...  (
(  \
\  )
)  (
(  \
\  )
)  (
( 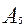 \
\  )... .
)... .
 = D
= D  (
(  \
\  )
)  (
(  \
\  )
)  (
(  \
\  )
)  ...=
...=
=D  (
(  \
\  )
)  (
(  \
\  )
)  (
( 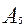 \
\  )...
)...  (
(  \
\  )
)  (
(  \
\ 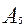 )
)  ... .
... .
Из полученных выражений для A и  , а так же из условий (1) следует A~
, а так же из условий (1) следует A~  , что и доказывает теорему.
, что и доказывает теорему.
|
из
5.00
|
Обсуждение в статье: Теорема Кантора о существовании множеств мощности более континуума |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

