 |
Главная |
Канонические уравнения кривых II порядка
|
из
5.00
|
При некотором специальном выборе осей координат уравнение (1) имеет более простые формы.
1. Эллипс. Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
 Т.к. точки F1, F2 заданы, то известно расстояние |F1F2| = 2c (фокусное расстояние). Для вывода уравнения эллипса выберем ось ОХ проходящей через фокусы, а начало координат – посередине отрезка F1F2.
Т.к. точки F1, F2 заданы, то известно расстояние |F1F2| = 2c (фокусное расстояние). Для вывода уравнения эллипса выберем ось ОХ проходящей через фокусы, а начало координат – посередине отрезка F1F2.
r1 = |MF1| и r2 = |MF2| - фокальные радиусы точки М. По определению: r1 + r2 = 2a (2a > 2c). Но  и
и  . Значит:
. Значит:  . Это и есть уравнение эллипса. Упростим его:
. Это и есть уравнение эллипса. Упростим его:



 ,
, 
Разделим на а2 – с2:  . Из
. Из  , т.е. а > c и значит, а2 – с2 > 0, поэтому обозначим а2 – с2 = b2. Окончательно:
, т.е. а > c и значит, а2 – с2 > 0, поэтому обозначим а2 – с2 = b2. Окончательно:
 (1)
(1)
 Это уравнение эллипса называется каноническим. Исследуем форму кривой по ее каноническому уравнению.
Это уравнение эллипса называется каноническим. Исследуем форму кривой по ее каноническому уравнению.
1. Из (1) следует, что эллипс – ограниченная кривая:  ;
;  ;
;  , т.е. все точки кривой содержатся в прямоугольнике с основанием 2а и высотой 2b.
, т.е. все точки кривой содержатся в прямоугольнике с основанием 2а и высотой 2b.
2. Если точка М1(х1, у1)  k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1)
k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1)  k, т.к. переменные х и у входят в (1) только в квадратах. Т.о., эллипс имеет две оси симметрии – ось ОХ и ось OY и центр симметрии – начало координат.
k, т.к. переменные х и у входят в (1) только в квадратах. Т.о., эллипс имеет две оси симметрии – ось ОХ и ось OY и центр симметрии – начало координат.
3. Найдем точки пересечения с осями координат:
х = 0  ; у = 0
; у = 0  . Если a > b, то
. Если a > b, то
|A1A2| = 2a – большая ось эллипса; |OA2| = a – большая полуось.
|B1B2| = 2b – малая ось эллипса; |OB2| = b – малая полуось.
4. Точки A1, A2, B1, B2 – вершины эллипса.
5. Для точек I четверти из (1):  . Когда х возрастает от 0 до а, то у уменьшается от b до 0.
. Когда х возрастает от 0 до а, то у уменьшается от b до 0.
 Замечание: В частном случае, если b = a = R, то (1) превращается в уравнение окружности: x2 + y2 = R2.
Замечание: В частном случае, если b = a = R, то (1) превращается в уравнение окружности: x2 + y2 = R2.
Отношение фокусного расстояния |F1F2| к длине большой оси |A1A2| называется эксцентриситетом. Эксцентриситет характеризует форму эллипса.  ,
,  , т.к. с< а, то
, т.к. с< а, то  . Фиксируем большую ось а эллипса и будем изменять
. Фиксируем большую ось а эллипса и будем изменять  . Т.к. b2 = a2 – c2, то
. Т.к. b2 = a2 – c2, то  , а
, а  .
.
Если  , то с уменьшается:
, то с уменьшается:  , т.е. фокусы сближаются. При этом
, т.е. фокусы сближаются. При этом  и эллипс в пределе превращается в окружность.
и эллипс в пределе превращается в окружность.
Если  , то
, то  и
и  , т.е. эллипс превращается в отрезок прямой.
, т.е. эллипс превращается в отрезок прямой.
2. Гипербола. Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
Выберем систему координат так же, как и при выводе уравнения эллипса: ось ОХ проходит через фокусы F1 и F2, а точка О делит расстояние между фокусами пополам:
 Обозначим: |F1F2| = 2c, тогда F1(c, 0); F2(-c, 0). Возьмем произвольную точку на гиперболе M(x, y). Тогда
Обозначим: |F1F2| = 2c, тогда F1(c, 0); F2(-c, 0). Возьмем произвольную точку на гиперболе M(x, y). Тогда  ;
;  . По определению гиперболы: r2 – r1 = ±2a. Знак «+», если r2 > r1, а знак «-», если r2 < r1. Или
. По определению гиперболы: r2 – r1 = ±2a. Знак «+», если r2 > r1, а знак «-», если r2 < r1. Или 
Это и есть уравнение гиперболы. Упростим его, избавившись от радикалов:
 ,
,  ,
,  ,
,  ,
,  .
.
Разделим на а2(с2 – а2):  . Из
. Из  : |F1F2| = 2c, а r1 – r2 =2a. По свойствам сторон треугольника: 2c > 2a; c > a: c2 – a2 > 0. Поэтому обозначим с2 – а2 = b2. Теперь уравнение гиперболы принимает канонический вид:
: |F1F2| = 2c, а r1 – r2 =2a. По свойствам сторон треугольника: 2c > 2a; c > a: c2 – a2 > 0. Поэтому обозначим с2 – а2 = b2. Теперь уравнение гиперболы принимает канонический вид:
 (2)
(2)
Исследуем это уравнение.
1. В отличие от эллипса, гипербола – неограниченная кривая:  . Все точки гиперболы лежат вне вертикальной полосы шириной 2а , а между прямыми х = -а и х = а кривая точек не имеет.
. Все точки гиперболы лежат вне вертикальной полосы шириной 2а , а между прямыми х = -а и х = а кривая точек не имеет.
 2. Если М1(х1, у1)
2. Если М1(х1, у1)  k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1)
k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1)  k, т.к. координаты х и у входят в уравнение (2) только в четных степенях. Поэтому, как и эллипс, гипербола имеет две оси симметрии – OX и OY и центр симметрии – начало координат.
k, т.к. координаты х и у входят в уравнение (2) только в четных степенях. Поэтому, как и эллипс, гипербола имеет две оси симметрии – OX и OY и центр симметрии – начало координат.
3. Точки пересечения с осями координат:
 , А1(-а, 0), А2(а, 0);
, А1(-а, 0), А2(а, 0);
 - кривая ось OY не пересекает (мнимая ось).
- кривая ось OY не пересекает (мнимая ось).
4. |A1A2| = 2a – действительная ось гиперболы; |OA2| = a – полуось;
|B1B2| = 2b – мнимая область; |OB2| = b – мнимая полуось.
5. Точки пересечения главных осей с гиперболой называются вершинами гиперболы. Гипербола имеет две вершины: А1(-а, 0) и А2(а, 0).
6. Для точек I четверти:  (
(  ). Если х изменяется от а до
). Если х изменяется от а до  , то у изменяется от 0 до
, то у изменяется от 0 до  и точка уходит по кривой в бесконечность.
и точка уходит по кривой в бесконечность.
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:  . Для гиперболы
. Для гиперболы  .
.
Асимптоты гиперболы.
Рассмотрим подробнее, как именно точка М по кривой уходит в бесконечность. Из (2):  . Если х неограниченно возрастает, то подкоренное выражение мало отличается от х2 и кривая почти не отличается от прямой
. Если х неограниченно возрастает, то подкоренное выражение мало отличается от х2 и кривая почти не отличается от прямой  .
.
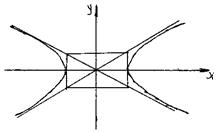 Т.о., при удалении точки М по кривой в бесконечность, она неограниченно приближается к одной из двух прямых:
Т.о., при удалении точки М по кривой в бесконечность, она неограниченно приближается к одной из двух прямых:  или
или  . Эти прямые называются асимптотами гиперболы.
. Эти прямые называются асимптотами гиперболы.
 Если a = b, то основным прямоугольником гиперболы будет квадрат и получаем равнобочную гиперболу: х2 – у2 = а2.
Если a = b, то основным прямоугольником гиперболы будет квадрат и получаем равнобочную гиперболу: х2 – у2 = а2.
Пример. Гипербола проходит через точку М1(1, 2), е = 3. Найти асимптоты.
 ;
;  ;
;  ;
;  ;
;
 ;
;
 ;
;  ;
;  ;
;  ; b = 2;
; b = 2;  ;
;  .
.
|
из
5.00
|
Обсуждение в статье: Канонические уравнения кривых II порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

