 |
Главная |
Вычисление обратной матрицы
|
из
5.00
|
Вычисление обратной матрицы осуществляется при помощи функция МОБР, принадлежащей категории Математические. Процесс вычисления обратной матрицы аналогичен вычислению произведения матриц.
Примечание. Обратной для А называется матрица В, если ее произведение с исходной А×В=Е, Е единичная матрица. Нахождение обратной матрицы – это, по существу, решение системы линейных уравнений.
Размещаем на листе матрицу (рис. 26) и обращаемся к соответствующей функции.
Активируем на листе ячейку, которая для матрицы обратной будет первым элементом, нажимаем F2, что покажет формулу, затем выделяем диапазон для результата, нажимаем Shft+Ctrl+Enter и получаем обратную матрицу (рис. 27). Правильность можно проверить с помощью произведения прямой и обратной. Получится единичная матрица.
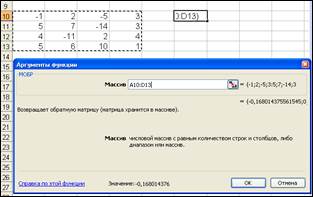
Рис. 26
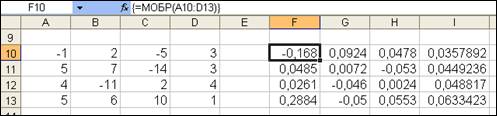
Рис. 27
Нахождение транспонированной матрицы
Категория функций Ссылки и массивы дает возможность получить транспонированные массивы, а именно такие, у которых индексы строк и столбцов меняются местами Аij=Tji (пример на рис. 28).
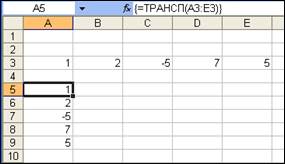
Рис. 28
Транспонируем матрицу Аij, в данном случаеA1:D4 (рис. 29), вызвав, функцию ТРАНСП категории Ссылки и массивы (рис. 30).
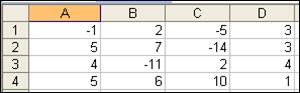
Рис. 29
Для транспонированной матрицы нужен диапазон (это второй массив).
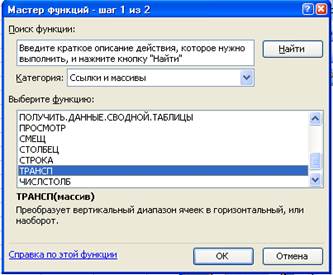
Рис. 30
Заполняем поле Массив (рис. 31).
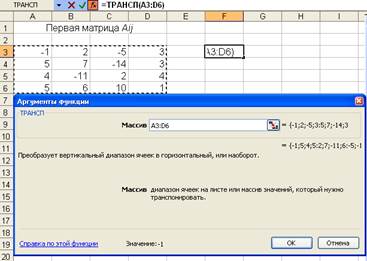
Рис. 31
Получаем первый элемент транспонированной матрицы, выделяем место под всю матрицу, начиная с первого полученного элемента. Нажимаем клавишу F2, затем Shft+Ctrl+Enter. Строки поменялись местами со столбцами (рис. 32).
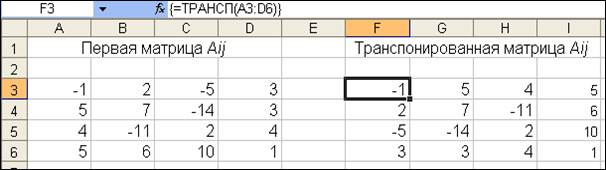
Рис. 32
Решение систем линейных уравнений
Применим функции МОБР, МУМНОЖ, МОПРЕД для решения систем линейных уравнений с несколькими неизвестными с помощью матричных функций в Excel (рис.33).
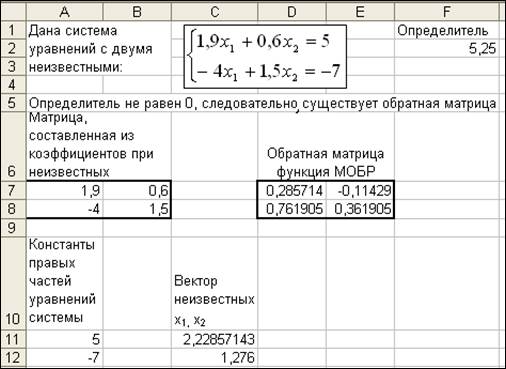
Рис. 33
Вектор неизвестных С11:С12 был получен с помощью функции МУМНОЖ обратной матрицы D7:E8 на столбец A11:A12.
ПРИСВОЕНИЕ ИМЕН ЯЧЕЙКАМ И МАССИВАМ
Имена ячеек и диапазонов используются в формулах для ссылок вместо абсолютных адресов. Чтобы присвоить имя ячейкам или диапазонам, нужно:
7) Выделить ячейку или диапазон. При выделении несмежных ячеек используется клавиша Ctrl (рис. 34).
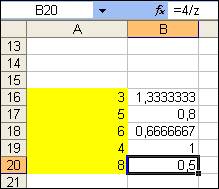
Рис. 34
8) Выбрать из меню Вставка – Имя – Присвоить (рис. 35а, 35б). (В MS Excel 10 это меню Формулы)
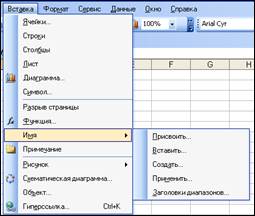
Рис. 35а
Присвоение имени в В MS Excel 2010
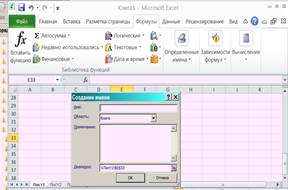
Рис. 35б
Присвоение имени в В MS Excel 2003
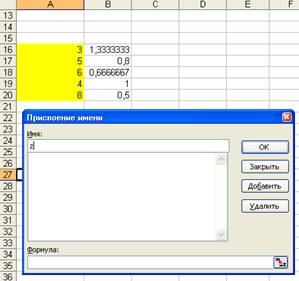
Рис. 36
Задания
Задание 1) Найти сумму элементов матрицы А, сумму элементов матрицы В, сумму соответствующих элементов матриц А и В, разность соответствующих элементов матриц А и В, определители, обратные матрицы и произведение матриц A и B. Вариант выбрать по последней цифре номера зачетной книжки из таблицы 1.
Таблица 1
| Вариант | Матрица А | Матрица В | |
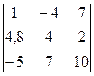
| 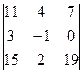
| ||
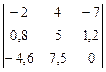
| 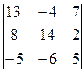
| ||
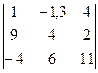
| 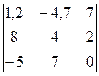
| ||
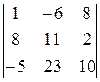
| 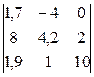
| ||
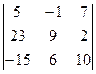
| 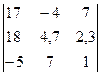
| ||
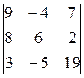
| 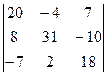
| ||
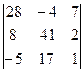
| 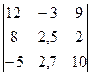
| ||
Окончание табл. 1
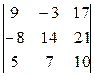
| 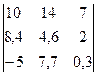
| |
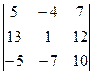
| 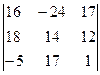
| |
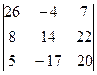
| 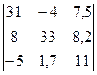
|
Задание 2) Найти решение системы трех линейных уравнений с тремя неизвестными. Вариант выбрать по последней цифре номера зачетной книжки из таблицы 1.
Таблица 2
| Вариант | Система уравнений | |
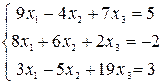
| ||
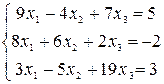
| ||
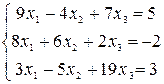
| ||
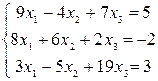
| ||
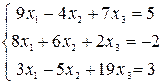
| ||
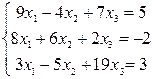
| ||
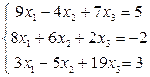
| ||
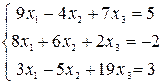
| ||
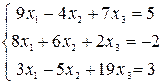
| ||
|
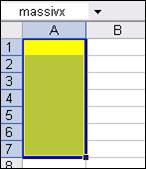
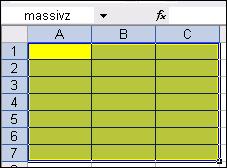
Задание 3) Присвоить массиву элементов А1:А7 имя massivx и массиву элементов А1:С7 имя massivz.
|
из
5.00
|
Обсуждение в статье: Вычисление обратной матрицы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

