 |
Главная |
Заметим, что для большего числа переменных формулы (1)-(3) естественным образом обобщаются
|
из
5.00
|
Если 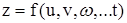 и
и 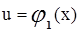 ,
,  , ... ,
, ... , 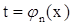 , то
, то
 (
( 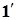 ) – полная производная.
) – полная производная.
Если 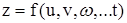 и
и 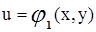 ,
,  ,...,
,..., 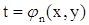 , то
, то
 ;
; 
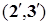 .
.
Заметим, что нужно делать различие в обозначении частных и обычных производных.
§6 Инвариантность формы полного дифференциала Ф.н.п.
Рассмотрим для простоты функцию двух переменных. z= f(u, v). Ее полный дифференциал, как мы видели, есть сумма частных дифференциалов:
 . (1)
. (1)
Это выражение (форма) полного дифференциала получено в предложении, что u и v независимые переменные. Докажем, что эта форма полного дифференциала сохраняется и в случае сложной функции, т.е. когда u и v есть сами функции, например, двух переменных: 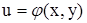 ,
, 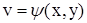 . Теперь имеем
. Теперь имеем
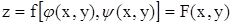 , x и y являются независимыми переменными. По определению полного дифференциала можем написать:
, x и y являются независимыми переменными. По определению полного дифференциала можем написать: 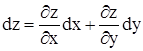 . Заменим
. Заменим 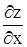 и
и 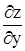 их выражениями
их выражениями 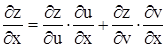 ;
;  . Получим: dz =
. Получим: dz = 
 . Перегруппируем слагаемые. Получим
. Перегруппируем слагаемые. Получим
dz = 
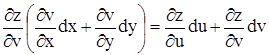 .
.
Итак, и в случае сложной функции полный дифференциал имеет форму (1), хотя смысл du и dv в этих случаях разный. В случае независимых u и v 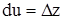 ,
, 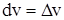 , а тут это целые выражения.
, а тут это целые выражения.
Аналогично для 
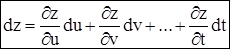 как при независимых аргументах u,v,...,t, так и при зависимых.
как при независимых аргументах u,v,...,t, так и при зависимых.
Свойство инвариантности формы полного дифференциала позволяет установить следующий факт. Для случая, когда u и v есть независимые переменные, или они есть функции от одной переменной, имеют место формулы:
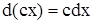 ;
;  ;
;  ,
,  .
.
Оказывается, что эти формулы справедливы и том случае, когда х и у являются функциями двух или большего числа переменных. Например, установим последнюю формулу. В силу инвариантности дифференциала будем его находить в форме (1), как будто, х и у независимые переменные:
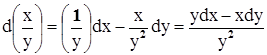 - то же, что и раньше.
- то же, что и раньше.
Пример  . Обозначим ху = u.
. Обозначим ху = u. 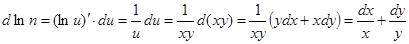 ,
,
 .
.
Отсюда, между прочим, сразу имеем  ,
,  .
.
§7 Производная от функции, заданной неявно.
Сначала рассмотрим неявную функцию одного переменного. Она определяется уравнением  (1), которое каждому х из некоторой области Х сопоставляет определённое у. Тогда на Х определяется этим уравнением функция у=f(х). Её называют неявной или неявно заданной. Если уравнение (1) удаётся разрешить относительно у, т.е. получить вид у=f(х), то задание неявной функции становится явным. Однако разрешить уравнение удается не всегда и в этом случае не всегда ясно – существует ли вообще неявная функция у=f(х), определяемая уравнением (1) в некоторой окрестности точки ( x0, y0 ).
(1), которое каждому х из некоторой области Х сопоставляет определённое у. Тогда на Х определяется этим уравнением функция у=f(х). Её называют неявной или неявно заданной. Если уравнение (1) удаётся разрешить относительно у, т.е. получить вид у=f(х), то задание неявной функции становится явным. Однако разрешить уравнение удается не всегда и в этом случае не всегда ясно – существует ли вообще неявная функция у=f(х), определяемая уравнением (1) в некоторой окрестности точки ( x0, y0 ).
Например, уравнение  неразрешимо относительно y и неясно - определяет ли оно неявную функцию в некоторой окрестности точки (1,0), например. Заметим, что существуют уравнения, не определяющие никакой функции (x2+y2+1=0).
неразрешимо относительно y и неясно - определяет ли оно неявную функцию в некоторой окрестности точки (1,0), например. Заметим, что существуют уравнения, не определяющие никакой функции (x2+y2+1=0).
Оказывается справедливой следующая теорема:
Теорема «Существования и дифференцируемости неявной функции» (без доказательства)
Пусть дано уравнение  (1) и функция
(1) и функция  , удовлетворяет условиям:
, удовлетворяет условиям:
1) Сама функция  и ее частные производные
и ее частные производные  и
и 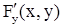 непрерывны в некоторой окрестности точки М0 (х0,у0);
непрерывны в некоторой окрестности точки М0 (х0,у0);
2)  ;
;
3) 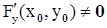 .
.
Тогда:
1) уравнение (1) при значении х близких к х0 определяет однозначную неявную функцию у=f(х);
2)  ;
;
3) эта функция непрерывна в окрестности точки х0;
4) она имеет непрерывную производную в этой окрестности, вычисляющуюся по формуле:
 . (2)
. (2)
Геометрически теорема утверждает, что в окрестности точки 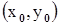 , где выполняемы условия теоремы, неявная функция, определяемая уравнением (1), может быть задана в явном виде у=f(х), т.к. каждому значению х соответствует единственное у. Если даже мы не можем найти выражение функции в явном виде, мы уверены, что в некоторой окрестности точки М0 это уже возможно в принципе.
, где выполняемы условия теоремы, неявная функция, определяемая уравнением (1), может быть задана в явном виде у=f(х), т.к. каждому значению х соответствует единственное у. Если даже мы не можем найти выражение функции в явном виде, мы уверены, что в некоторой окрестности точки М0 это уже возможно в принципе.
Рассмотрим тот же пример:  . Проверим условия:
. Проверим условия:
 1)
1)  ,
, 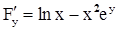 - и функция и её производные непрерывны в окрестности точки (1,0) (как сумма и произведение непрерывных).
- и функция и её производные непрерывны в окрестности точки (1,0) (как сумма и произведение непрерывных).
2) 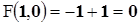 .
.
3)  . Значит, неявная функция у= f(х) существует в окрестности точки (1,0). Мы не можем её выписать в явном виде, но можем все-таки найти её производную, которая будет даже непрерывной:
. Значит, неявная функция у= f(х) существует в окрестности точки (1,0). Мы не можем её выписать в явном виде, но можем все-таки найти её производную, которая будет даже непрерывной:
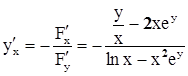
Рассмотрим теперь неявную функцию от нескольких переменных. Пусть задано уравнение
 . (2)
. (2)
Если каждой паре значений (х,у) из некоторой области уравнение (2) сопоставляет одно определённое значение z, то говорят, что это уравнение неявно определяет однозначную функцию от двух переменных  .
.
Справедлива и соответствующая теорема существования и дифференцирования неявной функции нескольких переменных.
Теорема 2: Пусть дано уравнение  (2) и функция
(2) и функция  удовлетворяет условиям:
удовлетворяет условиям:
1)  ,
,  ,
, 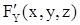 ,
, 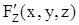 - существуют и непрерывны в некоторой окрестности точки
- существуют и непрерывны в некоторой окрестности точки 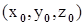 ;
;
2) 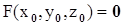 ;
;
3)  .
.
Тогда:
1) в некоторой окрестности точки М0 уравнение (2) определяет z как однозначную функцию от х,у:  ;
;
2)  ;
;
3) функция  непрерывна в этой окрестности;
непрерывна в этой окрестности;
4) неявная функция  имеет непрерывные частные производные в этой окрестности, вычисляемые по формулам:
имеет непрерывные частные производные в этой окрестности, вычисляемые по формулам: 
 .
.
Пример:  . Это уравнение задаёт z как двузначную неявную функцию от х и у
. Это уравнение задаёт z как двузначную неявную функцию от х и у 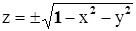 . Если проверить условия теоремы в окрестности точки, например, (0,0,1), то видим выполнение всех условий:
. Если проверить условия теоремы в окрестности точки, например, (0,0,1), то видим выполнение всех условий:
1) 
 - непрерывна,
- непрерывна, 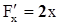 ,
,  ,
, 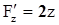 - непрерывны также;
- непрерывны также;
2) F(0,0,1)=1-1=0;
3) 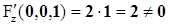 .
.
Значит, неявная однозначная функция существует в окрестности точки (0,0,1): Можно сказать сразу, что это  , задающая верхнюю полусферу.
, задающая верхнюю полусферу.
Существуют непрерывные частные производные  Они, кстати, получаются такими же, если дифференцировать неявную функцию, выраженную в явном виде, непосредственно.
Они, кстати, получаются такими же, если дифференцировать неявную функцию, выраженную в явном виде, непосредственно.
Определение и теорема существования и дифференцирования неявной функции большего числа аргументов аналогичны.
§8 Касательная плоскость и нормаль к поверхности. Геометрический смыл полного дифференциала функции двух
переменных.
Предварительно вспомним известные и выведем новые формулы для касательных и нормалей к плоским и пространственным кривым.
На плоскости:
Если кривая задана явной функцией y=f(x), то, как мы знаем, уравнение касательной к ней в точке (x0,y0) имеет вид:  , а уравнение нормали:
, а уравнение нормали:  .
.
Если кривая есть график функции, заданной неявно уравнением F(x,y)=0, то, как было показано, 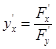 и потому уравнение касательной будет
и потому уравнение касательной будет  . Уравнение нормали:
. Уравнение нормали:  .
.
Если кривая задана параметрически:  то уравнение касательной имеет вид:
то уравнение касательной имеет вид: 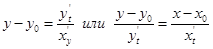 , уравнение нормали:
, уравнение нормали:  .
.
В пространстве наиболее употребительно задание кривой в параметрической форме:  Пусть дана точка Р0 (x0,y0,z0) на этой кривой, она соответствует параметру t0.
Пусть дана точка Р0 (x0,y0,z0) на этой кривой, она соответствует параметру t0.
Рассмотрим приращенную точку Р(x0+Dx, y0+Dy, z0+Dz) этой кривой, она соответствует значению параметра t0+Dt. Проведем секущую через точки Р0 и Р. Из аналитической геометрии известно, что уравнение этой секущей по двум точкам будет иметь вид 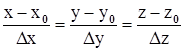 . Разделим все знаменатели на Dt
. Разделим все знаменатели на Dt  и перейдем к пределу при
и перейдем к пределу при 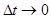 . Тогда секущая стремится к предельному положению – касательной и ее уравнение будет соответственно
. Тогда секущая стремится к предельному положению – касательной и ее уравнение будет соответственно  . Так как
. Так как  ,
, 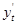 ,
, 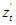 есть в этом уравнении координаты направляющего вектора касательной, то направляющие векторы касательной будут cos
есть в этом уравнении координаты направляющего вектора касательной, то направляющие векторы касательной будут cos  , cos
, cos 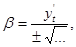 cos
cos  . Если рассмотрим теперь дифференциалы
. Если рассмотрим теперь дифференциалы  ,
, 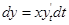 ,
,  , то видим пропорциональность этих дифференциалов направляющим косинусам касательной
, то видим пропорциональность этих дифференциалов направляющим косинусам касательной 

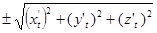
число
Перейдем теперь к рассмотрению касательной плоскости и нормали к поверхности. Пусть поверхность задана уравнением F(x, y, z)=0 и P0(x0, y0, z0) - точка на ней. Проведем на поверхности произвольную кривую L через точку P0. В параметрическом виде уравнение этой кривой будет  Так как кривая лежит на поверхности, то уравнения кривой должны удовлетворять уравнению поверхности: F
Так как кривая лежит на поверхности, то уравнения кривой должны удовлетворять уравнению поверхности: F 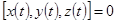 . Возьмем полный дифференциал от обеих частей. В силу инвариантности формы дифференциала можно записать
. Возьмем полный дифференциал от обеих частей. В силу инвариантности формы дифференциала можно записать 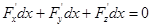 (1) или, заменяя дифференциалы на пропорциональные косинусы, перепишем
(1) или, заменяя дифференциалы на пропорциональные косинусы, перепишем 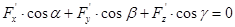 (2) (скалярное произведение в координатной форме). Равенство (2) можно рассматривать как условие перпендикулярности двух прямых. Одна из них является касательной к кривой L в точке P0,
(2) (скалярное произведение в координатной форме). Равенство (2) можно рассматривать как условие перпендикулярности двух прямых. Одна из них является касательной к кривой L в точке P0,  - ее направляющие косинусы. Тогда величины
- ее направляющие косинусы. Тогда величины  - есть величины, пропорциональные направляющим косинусам нормали к кривой L в точке P0. Но эти производные есть числа (они вычисляются в точке P0), поэтому они не зависят от кривой L и, значит, для любой кривой L, проходящей через точку P0 на поверхности, будут одними и теми же.
- есть величины, пропорциональные направляющим косинусам нормали к кривой L в точке P0. Но эти производные есть числа (они вычисляются в точке P0), поэтому они не зависят от кривой L и, значит, для любой кривой L, проходящей через точку P0 на поверхности, будут одними и теми же.
Но последнее означает, что нормаль ко всем касательным в точке P0 будет одна и та же, а это означает, что все касательные ко всевозможным кривым в точке P0 лежат в одной плоскости.
Эта плоскость - геометрическое место всех возможных касательных - и называется касательной плоскостью к поверхности в точке P0. А прямая, перпендикулярная касательной плоскости, называется нормалью к поверхности в точке P0. Вообще, уравнение любой плоскости, проходящей через точку P0, есть A(x-x0)+ B(y-y0)+ C(z-z0) = 0, где А,В,С величины пропорциональные направляющим косинусам нормали. Величины  ,
,  ,
,  - пропорциональны направляющим косинусам нормали, поэтому
- пропорциональны направляющим косинусам нормали, поэтому 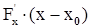 +
+ 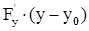

+ 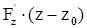 =0 (3) - уравнение касательной плоскости. Уравнение нормали запишется, очевидно, в виде
=0 (3) - уравнение касательной плоскости. Уравнение нормали запишется, очевидно, в виде 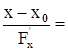
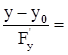
 (4). Все производные
(4). Все производные  ,
,  ,
,  есть числа, вычисляются в точке P0 (x0 ,y0, z0).
есть числа, вычисляются в точке P0 (x0 ,y0, z0).
Если поверхность задана явным уравнением z = f(x,y), то его можно переписать в виде f(x,y) – z = 0. Отсюда  +
+ 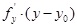 +
+ 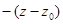 =0 (
=0 (  ,
, 

 (
( 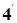 ) - уравнения касательной плоскости и нормали к поверхности, заданной в явном виде.
) - уравнения касательной плоскости и нормали к поверхности, заданной в явном виде.
Выясним теперь геометрический смысл полного дифференциала функции z = f(x,y). Из уравнения касательной плоскости (  имеем
имеем 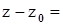
 +
+ 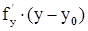 . Можем считать, что
. Можем считать, что  ,
, 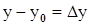 , тогда
, тогда 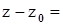

 . Но справа стоит полный дифференциал функции z = f(x,y), потому
. Но справа стоит полный дифференциал функции z = f(x,y), потому 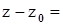 dx. Это равенство и позволяет выяснить геометрический смысл полного дифференциала dz.
dx. Это равенство и позволяет выяснить геометрический смысл полного дифференциала dz.
 Пусть в точке P0 (x0 ,y0, z0) проведена касательная плоскость. Передвигаясь по поверхности, перейдем в точку P (x0+
Пусть в точке P0 (x0 ,y0, z0) проведена касательная плоскость. Передвигаясь по поверхности, перейдем в точку P (x0+  ,y0+
,y0+  , z0+
, z0+ 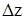 ) этой поверхности. В точке P0 аппликата z0=AP0. В точке P аппликата z=BP. Пусть AP0=BC. Тогда CP=
) этой поверхности. В точке P0 аппликата z0=AP0. В точке P аппликата z=BP. Пусть AP0=BC. Тогда CP= 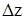 .
.
Если же из точки P0 по касательной плоскости перейдем в точку D, CD = z – z0; но 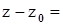 dx. Таким образом, полный дифференциал dz функции z = f(x,y) в точке (x0,y0) совпадет с приращением аппликаты точки на касательной плоскости к поверхности z = f(x,y) в точке P0 (x0 ,y0, z0). Из чертежа видно, что чем меньше
dx. Таким образом, полный дифференциал dz функции z = f(x,y) в точке (x0,y0) совпадет с приращением аппликаты точки на касательной плоскости к поверхности z = f(x,y) в точке P0 (x0 ,y0, z0). Из чертежа видно, что чем меньше  и
и  , тем меньше
, тем меньше 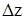 отличается от
отличается от 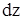 , что оправдывает равенство
, что оправдывает равенство 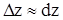 .
.
§9 Частные производные высших порядков.
Пусть функция z = f(x,y) определена в некоторой области D и имеет в ней частные производные 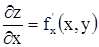 и
и  (1). Эти производные сами являются функциями от x,y. Поэтому они могут в некоторых точках области или во всех в свою очередь иметь частные производные, которые для исходной функции называются вторыми частными производными или частными производными второго порядка. Частные производные (1) называются частными производными первого порядка.
(1). Эти производные сами являются функциями от x,y. Поэтому они могут в некоторых точках области или во всех в свою очередь иметь частные производные, которые для исходной функции называются вторыми частными производными или частными производными второго порядка. Частные производные (1) называются частными производными первого порядка.
Частных производных второго порядка для функции двух переменных имеется 4:
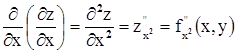 ;
; 


Каждая из вторых частных производных тоже является функцией и можно рассматривать их частные производные (их будет уже восемь), они называются - частные производные третьего порядка:
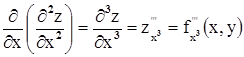 ,
,  и т.д.
и т.д.
Аналогично можно определять частные производные четвертого, пятого и т.д. порядков.
Частные производные высших порядков, взятых по разным аргументам, называются смешанными частными производными.
Пример: 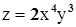 ,
,  ,
,  ,
,  ,
,  ,
, 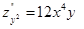 ,
,  ,
,  ,
,  ....
....
Из примера можно заметить, что смешанные производные по одним и те же аргументам оказались равны, хотя они взяты в разном порядке. Для данной функции это так, но для других это может и не выполнятся. Условие независимости смешанных производных от порядка дифференцирования дает:
Теорема (о равенстве смешанных производных). (без доказательства) Если функция z = f(x,y) и ее частные производные  ,
, 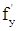 ,
, 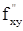 и
и  существуют и непрерывны в точке M (x,y) и некоторой ее окрестности, то в этой точке
существуют и непрерывны в точке M (x,y) и некоторой ее окрестности, то в этой точке 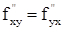 или
или 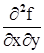 =
= 
Из теоремы, очевидно, что если непрерывны частные производные любого n-ого порядка, то они равны и поэтому порядок дифференцирования не важен. Можно писать  или
или 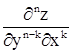 . Теорема верна и для функций большего числа переменных, смешанные частные производные равны, если они непрерывны. Поэтому и там пишут их в виде
. Теорема верна и для функций большего числа переменных, смешанные частные производные равны, если они непрерывны. Поэтому и там пишут их в виде  (k1+k2+k3=n) и w = f(x,y,z)
(k1+k2+k3=n) и w = f(x,y,z)
|
из
5.00
|
Обсуждение в статье: Заметим, что для большего числа переменных формулы (1)-(3) естественным образом обобщаются |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

