 |
Главная |
Функция распределения случайной величины, ее определение, свойства и график. Примеры
|
из
5.00
|
Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называется случайной величиной.
Если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
| x1 | x2 | … | xi | … |
| p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
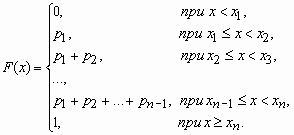
Свойства функции распределения.
1. 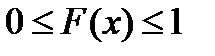 .
.
Доказательство:Это утверждение следует из того, что функция распределения – это вероятность, а как известно, 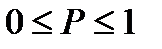 .
.
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
Доказательство: Пусть х1<x2. Докажем, что F(x1) 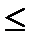 F(x2). Пусть событие А=(Х<x1), B=(x1
F(x2). Пусть событие А=(Х<x1), B=(x1 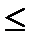 Х<x2). Тогда А+В=(Х<x2). События А и В несовместны, следовательно по теореме сложения Р(А+В)=P(А)+P(В). То есть Р(Х<x2) =Р(Х<x1)+Р(x1
Х<x2). Тогда А+В=(Х<x2). События А и В несовместны, следовательно по теореме сложения Р(А+В)=P(А)+P(В). То есть Р(Х<x2) =Р(Х<x1)+Р(x1 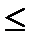 Х<x2). Другими словами F(x2)=F(x1)+ Р(x1
Х<x2). Другими словами F(x2)=F(x1)+ Р(x1 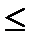 Х<x2). (3)
Х<x2). (3)
Так как Р(x1 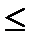 Х<x2)
Х<x2) 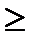
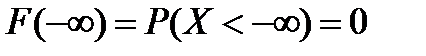 как вероятность невозможного события Х
как вероятность невозможного события Х 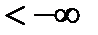 .
. 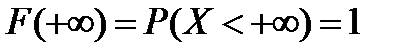 как вероятность достовероного события Х
как вероятность достовероного события Х 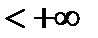 .
.
4. Р(х1 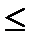 Х<x2)=F(x2)-F(x1). (4)
Х<x2)=F(x2)-F(x1). (4)
Доказательство:это непосредственно следует из формулы(3).
Пример: 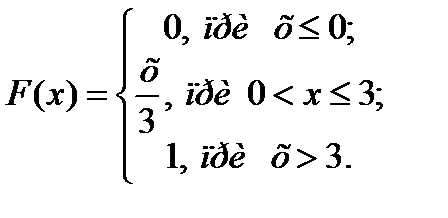 Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).
Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).
Решение:По формулеР(х1 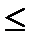 Х<x2)=F(x2)-F(x1). (4)
Х<x2)=F(x2)-F(x1). (4)
Р(2  Х<5)=F(5)-F(2)=1-2/3=1/3. (4).
Х<5)=F(5)-F(2)=1-2/3=1/3. (4).
Ответ : 1/3.
Функция распределения дискретной случайной величины. Примеры.
если - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
| x1 | x2 | … | xi | … |
| p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
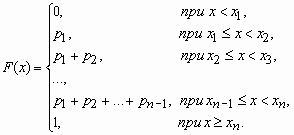
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
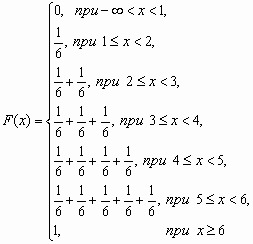

Теорема о существовании случайной величины с заданной функцией распределения. Непрерывная случайная величина. Вероятность отдельно взятого значения непрерывной случайной величины. Примеры.
Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). различают непрерывные и дискретные случайные величины.
Непрерывной случайной величиной называется случайная величина Х, если ее функция распределения (интегральная функция распределения) представима в виде:
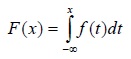
|
где f(x) – некоторая неотрицательная функция, такая что

|
Функция f(x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).
Вероятность того, что непрерывная случайная величина X принимает значение в заданном промежутке, вычисляется следующим образом:
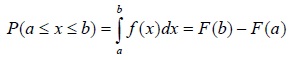
|
Примеры распределений вероятностей непрерывной случайной величины Х:
- равномерное распределение вероятностей непрерывной случайной величины;
- показательное распределение вероятностей непрерывной случайной величины;
- нормальное распределение вероятностей непрерывной случайной величины.
17. Абсолютно непрерывная случайная величина. Плотность вероятности абсолютно непрерывной случайной величины, ее определение, свойства, и график.
Важный класс непрерывных случайных величин -- абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.
Определение 3.7 Случайная величина 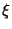 называется абсолютно непрерывной, если существует функция
называется абсолютно непрерывной, если существует функция 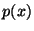 такая, что
такая, что
-
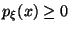 ,
, -
 ,
, -
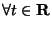 имеет место равенство:
имеет место равенство: 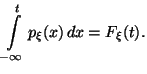
Функция 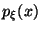 , обладающая вышеперечисленными свойствами, называется плотностью распределения случайной величины
, обладающая вышеперечисленными свойствами, называется плотностью распределения случайной величины 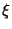 .
.
Следствие 3.1 Если 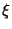 -- абсолютно непрерывная случайная величина, то
-- абсолютно непрерывная случайная величина, то
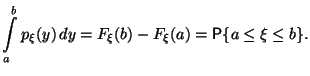
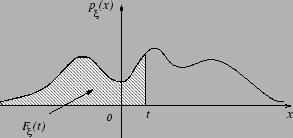
Наглядный смысл плотности можно проиллюстрировать следующим рисунком.
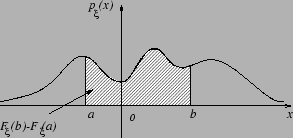
Замечание 3.5 Если плотность 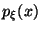 непрерывна в точке
непрерывна в точке 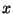 , то из Следствия 3.1вытекает следующее представление:
, то из Следствия 3.1вытекает следующее представление:
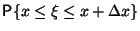
| 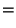
| 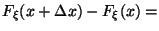
| |
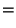
| 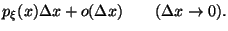
|
Следствие 3.2 Если 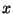 -- точка непрерывности функции
-- точка непрерывности функции 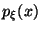 , то
, то
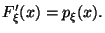
Примеры абсолютно непрерывных распределений
1) Равномерное распределение в отрезке 
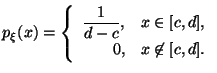
| 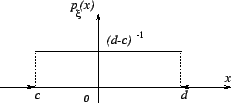
|
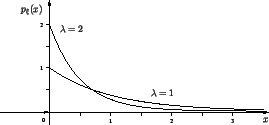
2) Показательное распределение с параметром 

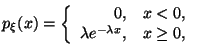
| 
|
Показательное распределение называют также экспоненциальным.
3) Нормальное (или гауссовское) распределение 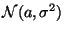 ,
, 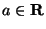 ,
,  :
:

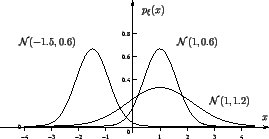
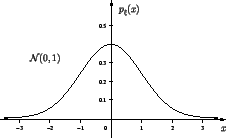
Стандартное нормальное распределение --  :
:

| 
|
Плотность распределения удовлетворяет свойствам:
 и
и  .
.
И наоборот, любая интегрируемая функция 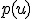 , удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
, удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием:
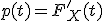 .
.
|
из
5.00
|
Обсуждение в статье: Функция распределения случайной величины, ее определение, свойства и график. Примеры |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

