Качественное рассмотрение поведения почти свободных электронов в кристалле

Рассмотрим, что происходит с энергией электронов в атомах, которые сначала находятся на больших расстояниях r (например, в газе), а затем сближаются до расстояния r_0,; которое соответствует расстоянию между атомами в кристалле и имеет порядок 10^-8 см = 10^-10 м = 1 Å (ангстрем).

В удаленных на большое расстояние r₁, т.е. в фактически невзаимодействующих атомах полная энергия электронов принимает, как известно из курса общей физики, только ряд определенных значений Е₁, Е₂, Е₂ и т.д., как это символично изображено на рис. 2-4, а. При r = r₀ кривые потенциальной энергии U(r)в промежутках между атомами накладываются друг на друга, и потенциальные барьеры, отделяющие электроны в соседних атомах, понижаются (рис. 2-4, б). В результате, электроны, находящиеся на уровнях Е₃ и более высоких, могут свободно перемещаться от атома к атому и поэтому принадлежат всему кристаллу.

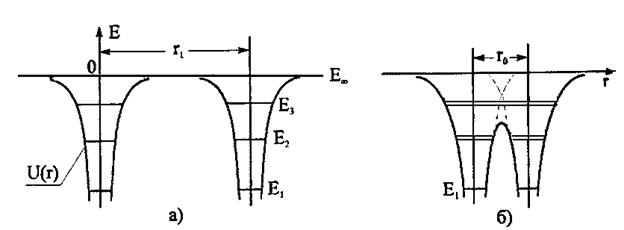
Рис. 2-4. Энергия электронов в удаленных атомах (а) и атомах, расположенных на расстоянии в несколько ангстрем (б)

Если число атомов в кристалле N, то все электроны, находящиеся на уровнях Е₃, могли бы оказаться в одном и том же состоянии, что запрещает принцип Паули. В действительности взаимодействие с соседними атомами приводит к изменению энергии электронов в каждом атоме, и уровень Е₃ расщепляется в простейшем случае на N близких подуровней, каждый из которых может быть занят двумя электронами с противоположными спинами. То же самое относится и к верхним уровням Е₄, Е₅ и т.д, а также к Е₂. Более глубокие уровни атома не расщепляются.

Интервал между подуровнями в каждой энергетической зоне составляет величину порядка 10^-23 эВ, т.е. подуровни расположены хотя и дискретно, но практически вплотную друг к другу.

Перемещаться по всему кристаллу могут не только электроны с энергией ~ Е₃, но и электроны, располагающиеся в энергетической зоне ~ Е₂, которые разделены в кристалле невысокими потенциальными барьерами (рис. 2-4, б). В результате туннельного эффекта электроны способны преодолевать эти барьеры, имеющие пространственную ширину порядка 1 Å, и также становиться общими для всего кристалла.

На рис. 2-5 описанные процессы сближения атомов при образовании кристаллов и соответствующие расщепления уровней качественно отражены в динамике.

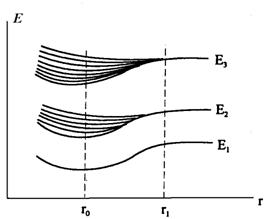
Рис. 2-5. Изменение энергии электронов по мере сближения атомов

до равновесного состояния в кристалле.

Таким образом, любое адекватное решение уравнения Шредингера должно продемонстрировать наличие раздельных разрешенных зон в энергетическом спектре электронов в кристалле, если наше качественные представления о происходящих процессах правильные. Это можно выяснить, привлекая, насколько возможно, строгую теорию для нахождения спектра электронов в кристалле.

Модель Кронига-Пенни

Для решения поставленной задачи, как уже было сказано, необходимо решить одноэлектронное уравнение Шредингера с периодическим потенциалом решетки U(r). Собственные функции (функции Блоха) ψ_k(r) и собственные значения E_k(r) этого уравнения в значительной мере зависят от вида периодического потенциала, точный вид которого определить практически невозможно. В этих условиях для нахождения решения уравнения Шредингера приходится применять различные приближенные методы, делая априорные предположения относительно вида функции U(r). Задача во всех случаях остается достаточно сложной, поэтому, не вникая на первых порах во все известные подходы, отметим, что некоторые характерные особенности энергетического спектра можно узнать, рассматривая одномерную модель периодического потенциала, предложенную Кронигом и Пенни.

В этой модели рассматривается движение электрона в линейной цепочке прямоугольных потенциальных ям, расположенных вдоль оси Х.. Ширина ям равна а, и они отделены друг от друга потенциальными барьерами толщиной b и высотой U₀. Длина цепочки равна L, а период цепочки равен c = a + b (рис. 2-6)

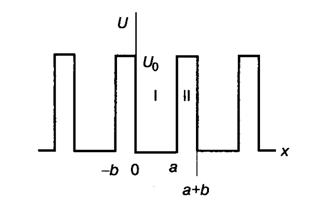
Рис. 2-6. Зависимость потенциальной энергии электрона от межатомного расстояния

в модели Кронига-Пенни.

Пусть Е – модель электрона. Состояние электрона здесь описывается одномерным уравнением Шредингера:

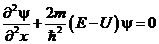
Для области I, где потенциальная энергия U = 0, волновая функция как решение этого уравнения может быть представлена в виде:

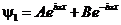
Первое слагаемое соответствует прямой волне, распространяющейся вдоль х, а второе – волне , отраженной от потенциального барьера.

В области II, где U = U₀, волновую функцию можно записать в виде:

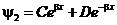
В приведенных решениях коэффициенты 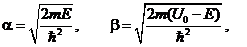величины A, B, C, D – некоторые константы.

Подставим вместо 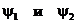одномерную функцию Блоха 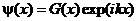и найдем вид периодической функции G(x) в областях I и II :

,

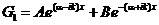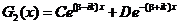
Для того чтобы определить коэффициенты A, B, C, D, используем тот факт, что функция G(x) и ее первая производная должны быть непрерывны в местах скачка потенциала. Например, в точке х = 0 имеем:

G₁(0) = G₂(0) и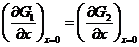

Кроме того, функции G(x) обладают свойством периодичности с периодом с = a + b и, следовательно, справедливы соотношения:

G₁(a) = G₂(-b) и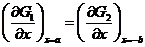

Подставляя эти условия в систему вышеприведенных уравнений для G₁(x) и G₂(x), получим четыре алгебраических уравнения (с правой частью, равной нулю) для определения коэффициентов A, B, C, D. Известно, что такая система уравнений будет иметь ненулевые решения при условии, что определитель, составленный из коэффициентов при A, B, C, D, будет равен нулю. Это требование приводит к уравнению (промежуточные выкладки опускаем) следующего вида:

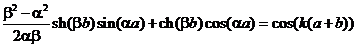
Это уравнение слишком сложно для прямого и полного анализа, поэтому исследуем его в некотором предельном случае, а именно, устремим ширину барьера b к нулю и увеличим высоту барьера U₀до бесконечности, но при условии, что произведение b∙U₀ остается постоянным. С точки зрения математики, можно сказать, что барьер аппроксимируется т.н. δ-функцией. Как следствие, теперь получаем, что при b→0 значения ch(βb)→1 и sh(βb)→βb. Таким образом, уравнение можно существенно упростить, представив его в виде:

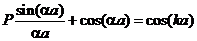, где P =

Параметр Р ~ abU₀представляет собой меру эффективной площади каждого барьера. Он характеризует степень непрозрачности барьера для электрона, или, другими словами, степень связанности электрона в потенциальной яме. Очевидно, что при стремлении Р→0 электрон становится свободным. Но нас интересуют как раз ситуации, где параметр Р достаточно высок (более единицы). Именно подобный случай отражен на рис. 2-7, где воспроизведена зависимость левой части последнего уравнения от значения ~ E^1/2.

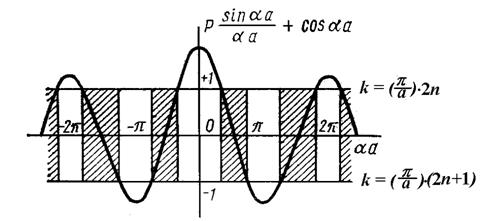
Рис. 2-7. Определение допустимых значений энергии электрона Е и значений модуля волнового вектора k, при которых возникают запрещенные энергетические зоны. Разрешенные зоны заштрихованы

Поскольку cos(ka), стоящий в правой части исследуемого уравнения, может принимать значения только в интервале от +1 до -1, то допустимыми значениями являются такие, для которых левая часть уравнения не выходит из указанных пределов. На рис. 2-7 графически показано образование разрешенных энергетических зон (заштрихованы) через аргумент , чередующихся с запрещенными энергетическими зонами.

В предположении Р >> 1 (т.е. U₀ >> E) можно получить явный вид закона дисперсии Е(k) для электрона, движущегося в периодическом поле одномерной решетки. Этот закон можно представить в обобщенном виде как

E = E_0M- C_M+ (-1)^MA_mcos(ka)

Здесь a – период решетки, значения М = 1, 2,…. Первый член дисперсионной зависимости E_0M представляет собой энергию М-го энергетического уровня электрона в изолированной бесконечно глубокой потенциальной яме, второй и третий члены связаны с действием периодического поля решетки. На рис. 2-8 показана зависимость Е(k) для электрона, находящегося в одномерной решетке (т.н. схема повторяющихся зон).

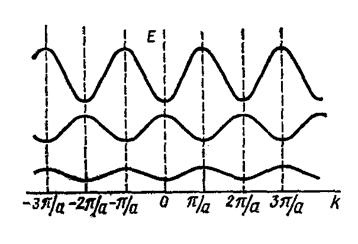
Рис. 2-8. Зависимость Е(k). Показаны первые три энергетические зоны.

Из рисунка наглядно видно, что для всех k, отличающихся на (2π/a)n, энергия одна и та же. Интервал значений k от –π/a до π/a представляет собой первую зону Бриллюэна, два отрезка от -2π/a до –π/a и от π/a до 2π/a – вторую зону Бриллюэна и т.д. Зонами Бриллюэна называют область k-пространства, внутри которой энергия электрона в кристалле изменяется квазинепрерывно.

Можно представить, по сути, аналогичную зависимость Е(k) в форме т.н. схемы расширенных зон, где изменение модуля волнового вектора k непрерывно, но учтены разрывы в энергетическом спектре (рис. 2-9). Здесь особенно наглядно видны отличия в спектре по сравнению со свободным электроном, где E = ћ²k² / 2m.

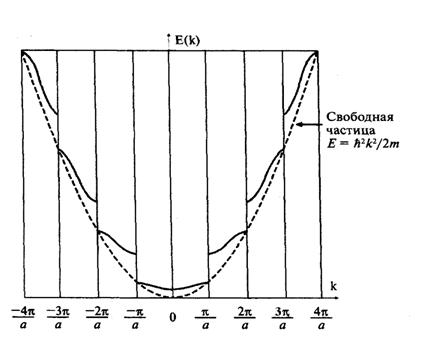
Рис. 2-9. Схема расширенных зон для зависимости Е(k)

Все возможные значения энергии в каждой энергетической зоне можно получить путем изменения k в пределах первой зоны Бриллюэна. Поэтому зависимость Е(k) часто строят только для первой зоны Бриллюэна. Все остальные значения Е могут быть приведены в эту зону. Такой способ изображения Е(k), показанный на рис. 2-10, получил название схемы приведенных зон.

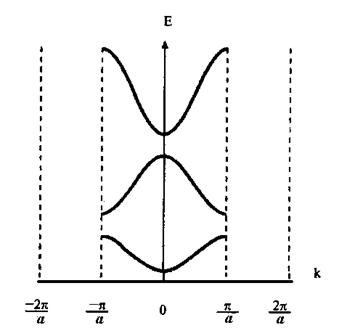
Рис. 2-10. Е(k) в представлении приведенных зон.

На границах зон Бриллюэна энергия терпит разрыв. Это хорошо видно на рис. 2-11, который представляет элемент расширенной зонной схемы. Здесь изображен энергетический разрыв при k = π / a

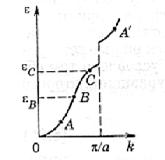
Рис. 2-11. Разрыв энергии при переходе из первой во вторую зону Бриллюэна.