 |
Главная |
Разработка факультативного занятия на тему «Способ рационализации при решении иррациональных уравнений»
|
из
5.00
|
Ход занятия
Иногда посредством некоторой подстановки удается привести иррациональное уравнение к рациональному виду. В таком случае говорят, что эта подстановка рационализирует рассматриваемое иррациональное уравнение, и называют ее рационализирующей.
Способ решения иррациональных уравнений, основанный на применении рационализирующих подстановок, назовем способом рационализации.
Применяя рационализирующую подстановку, необходимо следить за тем, чтобы область определения нового рационального уравнения, получаемого в результате этой подстановки, соответствовала области определения данного иррационального уравнения. Только при этом условии рационализирующая подстановка приведет рассматриваемое иррациональное уравнение к рациональному уравнению, которое всюду в области его определения эквивалентно данному.
Рассмотрим рационализацию некоторых выражений, содержащих радикалы, с помощью рационализирующих подстановок и применение этих подстановок при решении иррациональных уравнений.
1. Рационализация выражения 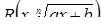
Выражение вида
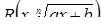 , (1)
, (1)
где 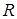 обозначает рациональную функцию,
обозначает рациональную функцию,  и
и  – постоянные, а
– постоянные, а  – любое целое положительное число, рационализируется подстановкой
– любое целое положительное число, рационализируется подстановкой
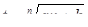 . (2)
. (2)
Действительно, возводя обе части равенства (2) в  -ую степень, получим
-ую степень, получим  , откуда
, откуда 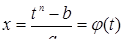 , причем функция
, причем функция 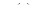 рациональна. Следовательно,
рациональна. Следовательно,
 .
.
Поскольку рациональная функция от рациональной функции представляет собой также рациональную функцию, то выражение, стоящее в правой части последнего равенства, является рациональным.
Пример 1. Решить уравнение 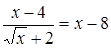 .
.
Решение. ОДЗ рассматриваемого уравнения 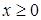 . Рационализирующей подстановкой
. Рационализирующей подстановкой 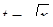
 это уравнение приводится к эквивалентной ему смешанной системе
это уравнение приводится к эквивалентной ему смешанной системе
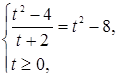
или (сокращая дробь на 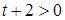 ) системе
) системе
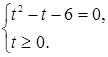
Решением последней будет 
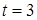 . Воспользовавшись подстановкой, получим
. Воспользовавшись подстановкой, получим 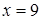 .
.
Ответ: 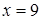 .
.
2. Рациональность дробно-линейных иррациональностей
Аналогично предыдущему доказывается, что функция вида
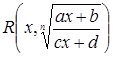 , (3)
, (3)
где  ,
,  ,
, 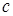 и
и  – некоторые постоянные, а
– некоторые постоянные, а  – любое целое положительное число (дробно-линейная иррациональность), может быть при условии
– любое целое положительное число (дробно-линейная иррациональность), может быть при условии 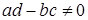 приведена к рациональному виду подстановкой
приведена к рациональному виду подстановкой
 (4)
(4)
Иррациональная функция
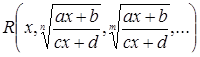 (5)
(5)
рационализируется при помощи подстановки
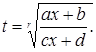 (6)
(6)
где 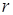 – наименьшее общее кратное показателей радикалов
– наименьшее общее кратное показателей радикалов  ,
, 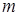 , …
, …
Пример 2. Решить уравнение 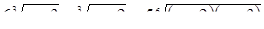 .
.
Решение. Будем искать корни данного уравнения в области 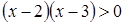 (очевидно, что числа
(очевидно, что числа 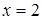 и
и 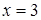 не являются его корнями). Разделим обе части уравнения на
не являются его корнями). Разделим обе части уравнения на 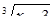 :
:
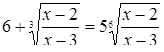 .
.
Полученное уравнение в рассматриваемой области с помощью рационализирующей подстановки
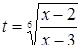
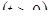
сводится к смешанной системе
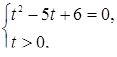
эквивалентной ему в этой области. Определив решения этой системы 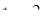 и
и 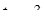 и воспользовавшись подстановкой, находим корни исходного уравнения.
и воспользовавшись подстановкой, находим корни исходного уравнения.
Ответ: 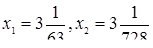 .
.
3. Рационализация биноминальных выражений
Можно доказать, что выражение
 , (7)
, (7)
где  и
и  – постоянные, а показатели степеней
– постоянные, а показатели степеней 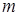 ,
,  – некоторые рациональные числа, допускает рационализирующие подстановки только в трех случаях, когда оказывается целым одно из чисел
– некоторые рациональные числа, допускает рационализирующие подстановки только в трех случаях, когда оказывается целым одно из чисел 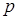 ,
,  или
или 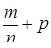 .
.
В этих случаях возможны следующие подстановки:
Если 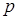 – целое, то
– целое, то 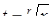 , где
, где 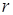 – наименьшее общее кратное знаменателей чисел
– наименьшее общее кратное знаменателей чисел 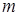 и
и  .
.
Если  – целое, то
– целое, то 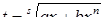 , где
, где 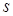 – знаменатель числа
– знаменатель числа 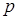 .
.
Если 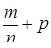 – целое, то
– целое, то 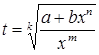 , где
, где 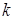 – знаменатель числа
– знаменатель числа 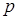 .
.
Существование указанных трех рационализирующих подстановок доказывает возможность приведения к рациональному виду уравнений 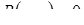 в первом случае и
в первом случае и 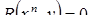 во втором и третьем случаях.
во втором и третьем случаях.
Пример 3. Решить уравнение 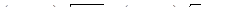 .
.
Решение. Так как 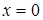 – не является корнем уравнения, разделим обе его части на
– не является корнем уравнения, разделим обе его части на 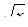 . Выделяется биномиальное выражение:
. Выделяется биномиальное выражение:
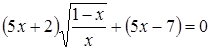 .
.
Имеет место третий случай рационализации ( 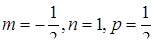 и
и 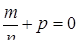 – целое число). Следовательно, будем применять подстановку
– целое число). Следовательно, будем применять подстановку 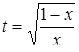
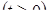 . Возводя обе части этого равенства в квадрат, получим
. Возводя обе части этого равенства в квадрат, получим 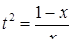 , так что
, так что 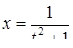 . Теперь с помощью подстановки
. Теперь с помощью подстановки 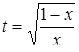 и найденного значения
и найденного значения  получаем
получаем
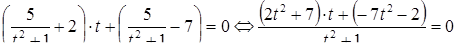
и исходное иррациональное уравнение приводится к рациональному  , или
, или 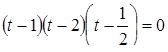 . Определив корни этого уравнения
. Определив корни этого уравнения 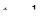
 ,
, 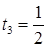 и воспользовавшись подстановкой, находим
и воспользовавшись подстановкой, находим 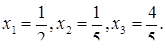
Ответ: 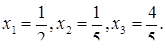
4. Рационализация квадратичныхиррациональностейпосредством подстановок Эйлера
Квадратичной иррациональностью назовем функцию вида
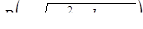 , (9)
, (9)
где 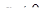
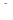 и
и 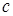 – некоторые постоянные. Покажем, что это выражение всегда рационализируется одной из так называемых подстановок Эйлера. При этом мы, конечно, будем считать, что квадратный трёхчлен
– некоторые постоянные. Покажем, что это выражение всегда рационализируется одной из так называемых подстановок Эйлера. При этом мы, конечно, будем считать, что квадратный трёхчлен 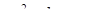 неотрицателен и не имеет равных корней (в противном случае корень можно заменить рациональным выражением).
неотрицателен и не имеет равных корней (в противном случае корень можно заменить рациональным выражением).
а) Сначала рассмотрим случай, когда дискриминант 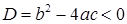 . В этом случае знак квадратного трёхчлена
. В этом случае знак квадратного трёхчлена 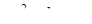 совпадает со знаком
совпадает со знаком  , и поскольку этот трёхчлен положителен (в силу условия
, и поскольку этот трёхчлен положителен (в силу условия  равенство трёхчлена нулю невозможно), то
равенство трёхчлена нулю невозможно), то 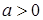 .
.
Таким образом, мы можем сделать следующую подстановку:
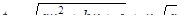
(или 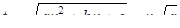 ) (10)
) (10)
Подстановку (10) иногда называют первой подстановкой Эйлера. Докажем, что эта подстановка рационализирует функцию (9) в рассматриваемом случае. Возводя в квадрат обе части равенства
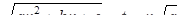
(заметим, что 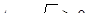 ), получим
), получим 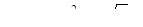 , так что
, так что
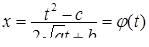 ,
,
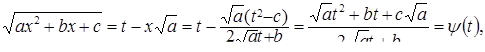
где функции  и
и 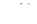 рациональные. Таким образом,
рациональные. Таким образом,
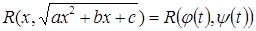 .
.
В правой части полученного равенства стоит рациональная функция.
б) Рассмотрим теперь случай, когда дискриминант 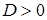 , то есть квадратный трехчлен
, то есть квадратный трехчлен 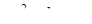 имеет (различные) действительные корни
имеет (различные) действительные корни  и
и  . Следовательно,
. Следовательно,
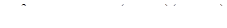 .
.
Аналогично предыдущему доказывается, что в этом случае функция (9) рационализируется посредством подстановки:
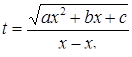
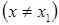 , (11)
, (11)
называемой часто второй подстановкой Эйлера.
Замечание 1. Рационализирующая подстановка (11) справедлива при условии 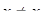 . Следовательно, применяя эту подстановку при решении иррационального уравнения, необходимо проверить, не является ли значение
. Следовательно, применяя эту подстановку при решении иррационального уравнения, необходимо проверить, не является ли значение 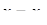 корнем данного уравнения (иначе возможна потеря этого корня).
корнем данного уравнения (иначе возможна потеря этого корня).
Замечание 2. Если 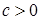 , то в этом случае можно положить
, то в этом случае можно положить
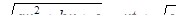
(или 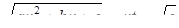 ) (12)
) (12)
Ответ: 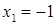 ,
, 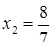 .
.
Пример 4. Решить уравнение 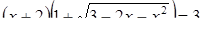 .
.
Решение. В данном уравнении дискриминант квадратного трехчлена положителен, корни его 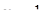 и
и  . Найдем другие корни подстановкой
. Найдем другие корни подстановкой
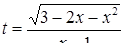 .
.
Применяя эту подстановку, необходимо проверить, не является ли значение  корнем данного уравнения. Итак,
корнем данного уравнения. Итак,  – корень данного уравнения.
– корень данного уравнения.
Возводя в квадрат обе части равенства 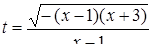 , получим
, получим  , откуда
, откуда 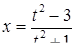 . Теперь подставим это значение
. Теперь подставим это значение  в исходное уравнение и последовательно получаем:
в исходное уравнение и последовательно получаем:
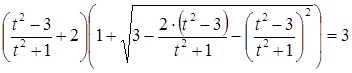
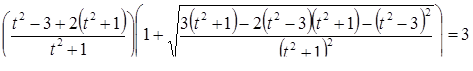

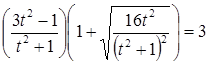

и исходное уравнение сводится к уравнению 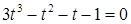 , или
, или 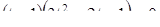 . Это уравнение имеет единственный действительный корень
. Это уравнение имеет единственный действительный корень 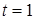 , тогда
, тогда  . Итак, исходное уравнение имеет два корня:
. Итак, исходное уравнение имеет два корня:  и
и 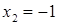 .
.
Ответ:  ,
, 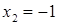 .
.
5. Рационализация с помощью тригонометрических подстановок
Иногда подходящей заменой неизвестной иррациональное уравнение можно свести к тригонометрическому уравнению. При этом полезными могут оказаться следующие замены переменной. [17]
1). Если в уравнение входит радикал 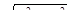 , то можно сделать замену
, то можно сделать замену 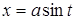 ,
, 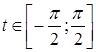 или
или 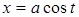 ,
, 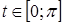 .
.
2). Если в уравнение входит радикал 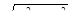 , то можно сделать замену
, то можно сделать замену 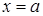 tg t,
tg t,  или
или 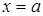 ctg t,
ctg t, 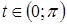 .
.
3). Если в уравнение входит радикал 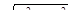 , то можно сделать замену
, то можно сделать замену  ,
,  или
или 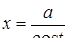 ,
, 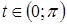 .
.
Проиллюстрируем использование этих замен на следующих примерах.
Пример 5. Решить уравнение 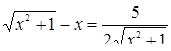 .
.
Решение. В данное уравнение входит выражение  , поэтому в соответствии с пунктом 2, сделаем замену
, поэтому в соответствии с пунктом 2, сделаем замену
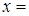 tg t, где
tg t, где  .
.
Тогда выражение  , входящее в уравнение, можно преобразовать
, входящее в уравнение, можно преобразовать
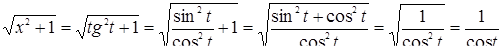
и исходное уравнение можно записать в виде
 .
.
Поскольку 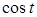 не равен нулю при рассматриваемых значениях t, то полученное уравнение равносильно уравнению
не равен нулю при рассматриваемых значениях t, то полученное уравнение равносильно уравнению
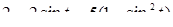 .
.
Решая это уравнение, находим два возможных значения
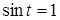 и
и 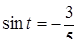 .
.
Из всех корней этих уравнений промежутку 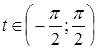 принадлежит единственное значение
принадлежит единственное значение 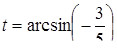 .
.
Поэтому соответствующее значение x равно
 .
.
Ответ. 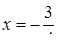 .
.
Пример 6. Решить уравнение 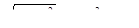 .
.
Решение. В этом уравнении x по ОДЗ может принимать только значения из отрезка 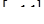 , что приводит к мысли совершить замену
, что приводит к мысли совершить замену
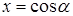 , где
, где 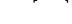 .
.
В результате такой замены приходим к уравнению
 .
.
Учтем, что
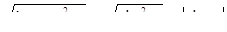 и
и  ,
,
получим уравнение
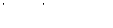 .
.
В силу ограничения 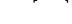 выполнено
выполнено 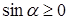 , поэтому приходим к уравнению
, поэтому приходим к уравнению
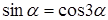 ,
,
которое, пользуясь формулой приведения, сведем к стандартному виду
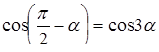 .
.
Решая последнее уравнение, находим
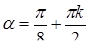 или
или  ,
, 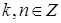 .
.
Условию 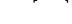 удовлетворяют лишь три значения
удовлетворяют лишь три значения
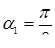 ,
,  ,
, 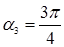 .
.
Поэтому
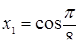 ,
, 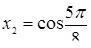 ,
, 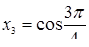 .
.
Ответ. 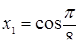 ,
, 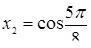 ,
, 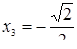 .
.
В заключение нужно отметить, что способ рационализации успешно может быть применён также для рационализации иррациональных неравенств, для вычисления и преобразования иррациональных выражений и так далее.
|
из
5.00
|
Обсуждение в статье: Разработка факультативного занятия на тему «Способ рационализации при решении иррациональных уравнений» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

