Метод простой итерации

Этот метод широко используется для численного решения уравнений и их систем различных видов. Рассмотрим применение метода простой итерации к решению систем линейных уравнений.

Запишем исходную систему уравнений в векторно-матричном виде  и выполним ряд тождественных преобразований:

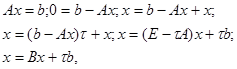
Где 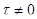- некоторое число, Е - единичная матрица, .

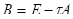Получившаяся система эквивалентна исходной системе и служит основой для построения метода простой итерации.

Выберем некоторое начальное приближение  и поставим в правую часть системы:

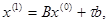
Поскольку  не является решением системы, в левой части получится некоторый столбец , в общем случае отличный от . Полученный столбец  будем рассматривать в качестве следующего (первого) приближения к решению. Аналогично, по известному k-му приближению можно найти (k+1) - е приближение:

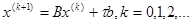
Эта формула и выражает собой метод простой итерации. Для ее применения нужно задать неопределенный пока параметр . От значения 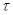 зависит, будет ли сходится метод, а если будет, то какова будет скорость сходимости, т.е. как много итераций нужно совершить для достижения требуемой точности. В частности справедлива следующая теорема.

Теорема. Метод простой итерации сходится тогда и только тогда, когда все собственные числа матрицы  по модулю меньше единицы.

Для некоторых типов матрицы А можно указать правило выбора 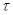, обеспечивающее сходимость метода и оптимальную скорость сходимости. В простейшем случае  можно положить равным некоторому постоянному числу, например, 1, 0.1 и т.д.

Метод Зейделя

Этот метод можно проиллюстрировать на примере решения системы:

a₁₁x₁+a₁₂x₂+a₁₃x₃=b₁

a₂₁x₁+a₂₂x₂+a₂₃x₃=b₂

a₃₁ x₁+ a₃₂ x₂+ a₃₃ x₃= b₃

Предположим, что диагональные элементы a₁₁, a ₂₂, a ₃₃ отличны от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х₁, х₂, х₃ соответственно из первого, второго и третьего уравнений системы:

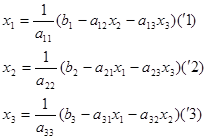
Зададим некоторые начальные (нулевые) приближения значений неизвестных: х₁=х₁ ^(0), х₂=х₂ ^(0), х₃=х₃ ^(0). Подставляя эти значения в правую часть выражения (‘1), получаем новое (первое) приближение для х₁:

Используя это значение для х₁ и приближение х₃ ⁽⁰⁾ для х₃, находим из (‘2) первое приближение для х₂:

.

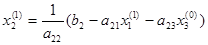И наконец, используя вычисленные значения х₁=х₁ ^(1), х₂=х₂ ^(1), находим с помощью выражения (‘3) первое приближение для х₃:

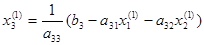
На этом заканчивается первая итерация решения системы (‘1) (‘2) (‘3). Используя теперь значения х₁ ^(1), х₂ ^(1), х₃ ^(1), можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению х₁=х₁ ^(2), х₂=х₂ ^(2), х₃=х₃ ⁽²⁾ и т.д.

Приближение с номером с k можно вычислить, зная приближение с номером k-1, как

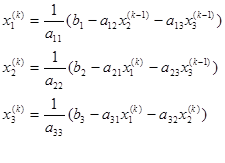
Итерационный процесс продолжается до тех пор, пока значения х₁ ^{( k),} х₂ ^{( k),} х₃ ^{( k)} не станут близкими с заданной погрешностью к значениям х₁ ^{( k-1),} х₂ ^{( k-1),} х₃ ^{( k-1).}