 |
Главная |
Свойства определителей. 1. Определитель не меняется при транспонировании
|
из
5.00
|
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j= 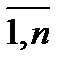 ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
МиноромMi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j.
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки d = ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i = 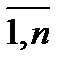 )
)
или j- го столбца d = a1 j A1 j + a2 j A2 j +... + an j An j (j = 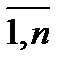 ).
).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример 1.4.Не вычисляя определителя 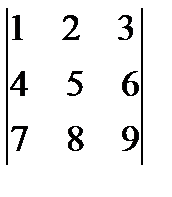 , показать, что он равен нулю. Решение. Вычтем из второй строки первую, получим определитель
, показать, что он равен нулю. Решение. Вычтем из второй строки первую, получим определитель 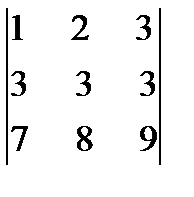 , равный исходному. Если из третьей строки также вычесть первую, то получится определитель
, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 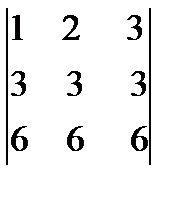 , в котором две строки пропорциональны. Такой определитель равен нулю.
, в котором две строки пропорциональны. Такой определитель равен нулю.
Пример 1.5.Вычислить определитель D = 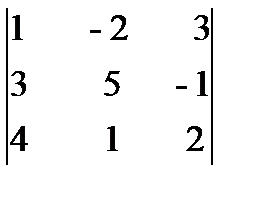 , разложив его по элементам второго столбца.
, разложив его по элементам второго столбца.
Решение. Разложим определитель по элементам второго столбца:
D = a12A12 + a22A22+a32A32=
= 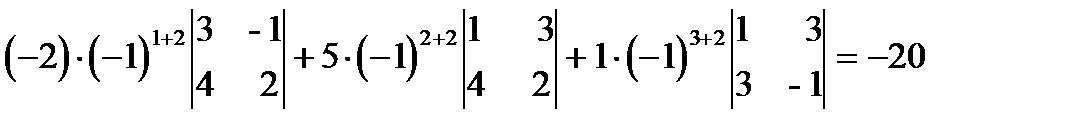 .
.
Пример 1.6. Вычислить определитель
A = 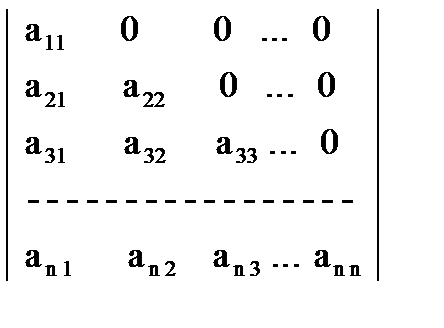 ,в котором все элементы по одну сторону от главной диагонали равны нулю. Решение. Разложим определитель А по первой строке: A = a11 A11 =
,в котором все элементы по одну сторону от главной диагонали равны нулю. Решение. Разложим определитель А по первой строке: A = a11 A11 = 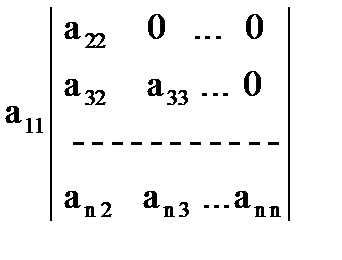 . Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
. Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
A = 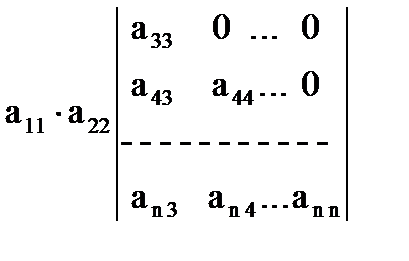 .И так далее. После n шагов придем к равенству A = а11 а22... ann.
.И так далее. После n шагов придем к равенству A = а11 а22... ann.
3.Основные понятия систем линейных уравнений. Теорема Крамера.
Определение. Система линейных уравнений — это объединение из n линейныхуравнений, каждое из которых содержит k переменных. Записывается это так:
 Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что числоуравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что числоуравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
Определение. Решение системы уравнений — это последовательность чисел (k1,k2, ..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2, ..., xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
1. Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решатьсистему.
2. Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
3. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Определение. Переменная xi называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
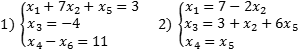
Обе системы являются разрешенными относительно переменных x1, x3 и x4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x1, x3 и x5. Достаточно переписать самое последнее уравнение в видеx5 = x4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
1. Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такаясистема является совместной и определенной, т.к. x1 = b1, x2 = b2, ..., xk = bk;
2. Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x2, x5, x6 (для первой системы) и x2, x5(для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы…
Как решить?: – Решение системы линейных уравнений методом подстановки («школьный метод»).
– Решение системы методом почленного сложения (вычитания) уравнений системы.
–Решение системы по формулам Крамера.
–Решение системы с помощью обратной матрицы.
–Решение системы методом Гаусса.
КРАМЕР
Сначала рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений 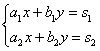
На первом шаге вычислим определитель 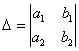 , его называют главным определителем системы.
, его называют главным определителем системы.
Если 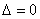 , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
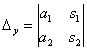 Если
Если 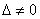 , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя: 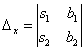 и
и
На практике вышеуказанные определители также могут обозначаться латинской буквой 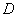 .
.
Корни уравнения находим по формулам:, 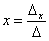
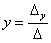
Пример 7
Решить систему линейных уравнений
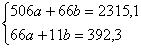
Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
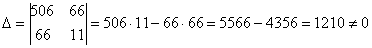 , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
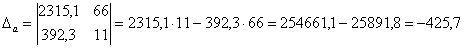 ;
;
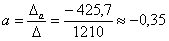
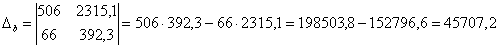 ;
; 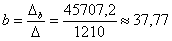
Ответ: 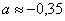 ,
, 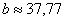
Как видите, корни получились иррациональными, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательнымфрагментом оформления задания является следующий фрагмент: « 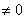 , значит, система имеет единственное решение». В противном случае рецензент может Вас наказать за неуважение к теоремеКрамера.
, значит, система имеет единственное решение». В противном случае рецензент может Вас наказать за неуважение к теоремеКрамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения 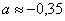
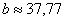 в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
ИЛИ:
Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
D = det (ai j)
и n вспомогательных определителей D i (i= 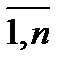 ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
D × x i = D i (i = 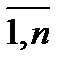 ). (5.4)
). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = D i / D.
Если главный определитель системы D и все вспомогательные определители D i = 0 (i= 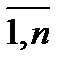 ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример 1.14. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5, x1 + 2x2 - x3 + 4x4 = -2, 2x1 - 3x2 - x3 - 5x4 = -2, 3x1 + x2 +2x3 + 11 x4 = 0.
Решение. Главный определитель этой системы D = 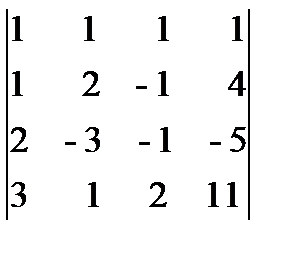 = -142 ¹ 0, значит, система имеет единственное решение. Вычислим вспомогательные определители D i (i=
= -142 ¹ 0, значит, система имеет единственное решение. Вычислим вспомогательные определители D i (i= 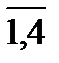 ), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов: D 1 =
), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов: D 1 = 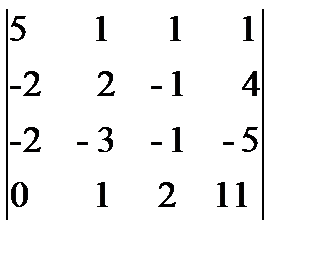 = - 142, D 2 =
= - 142, D 2 = 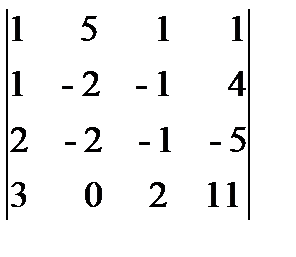 = - 284, D 3 =
= - 284, D 3 = 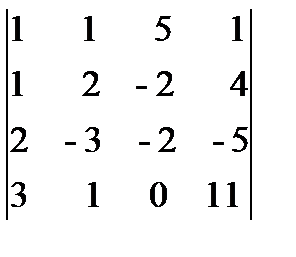 = - 426,
= - 426,
D 4 = 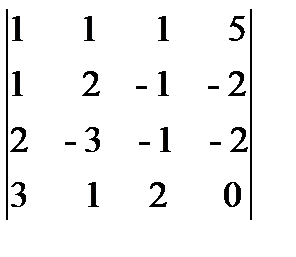 = 142. Отсюда x1 = D 1/D = 1, x2 = D 2/D = 2, x3 = D 3/D = 3, x4 = D 4/D = -1, решение системы - вектор С=(1, 2, 3, -1)T.
= 142. Отсюда x1 = D 1/D = 1, x2 = D 2/D = 2, x3 = D 3/D = 3, x4 = D 4/D = -1, решение системы - вектор С=(1, 2, 3, -1)T.
Основные понятия систем линейных уравнений. Метод гаусса.
СМОТРИ ВЫШЕ.
Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса.
Алгоритм
1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.
2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
3. Все элементы первой строки делят на верхний элемент выбранного столбца.
4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.
5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
6. После повторения этой процедуры 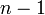 раз получают верхнюю треугольную матрицу
раз получают верхнюю треугольную матрицу
7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).
9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.
Метод Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 1.13. Решить систему уравнений методом Гаусса:x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
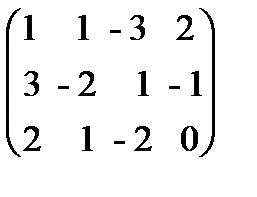 и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: 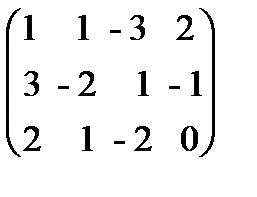 ~
~ 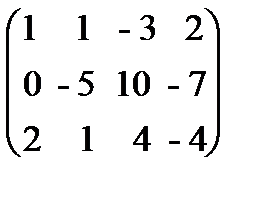 ;
;
б) третью строку умножим на (-5) и прибавим к ней вторую: 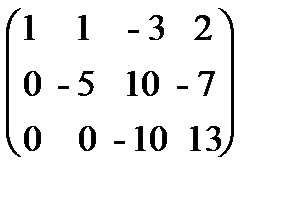 .
.
В результате всех этих преобразований данная система приводится к треугольному виду: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = - 0,7
ИЗ ТЕТРАДИ:
Метод Гаусса
Метод состоит из двух частей- прямого и обратного хода.
Прямой ход заключается в поведение расширение матрицы СЛУ к ступенчатому виду с помощью элементарных преобразований строк. В ступенчатом виде матрице каждая последующая строка имеет в начале нулей больше, чем предыдущая – или она нулевая
Пример:
Элементарные преобразование строк матрицы- это:
1)прибавление чисел одной строки матрицы, умножены на какое-нибудь число, к одной из нижних строк матрицы.
2)Перемена двух строчек местами
Обратный ход метод Гаусса заключается в последовательном выражении одних переменных через других, начиная с нижней нулевой строки. В результате получается общее решение.
После прямого хода возможны 3 варианта ступенчатого вида расширенной матрицы:
1)Каждая след.строка имеет в начале ровно не один ноль больше, чем предыдущая
Пример:
Записываем по строчкам уравнение и начинаем находить значение переменных с нижней строчки.
4Х4=8Þ Х4=2
Подставляем в предыдущее уравнение
2Х3-3Х4=-8 т.е. 2Х3-3*2=-8 или 2Х3=-2, Þ Х3=-1 , подставляем Х3 и Х4 во вторую строчку и т.д. Получаем единственно решение СЛУ
2) Число ненулевых строк меньше числа переменных. Тогда одни из строк содержит в начале нулей по крайней мере на 2 больше предыдущей и считаем, что последующая ненулевая строка не имеет вид(0…0 b) где число b=0
Например:
3) Последняя ненулевая строка имеет вид (0…0/b),где b=0 ей соответствует противоречивые равенства о=b,поэтому система несовместима
Решение СЛУ методом Гаусса
2Х1+3Х2+Х3=1
4Х1+5Х2+4Х3=7
6Х1+10Х2-3Х3=-10
Составляем расширенную матрицу прямой ход.
|
из
5.00
|
Обсуждение в статье: Свойства определителей. 1. Определитель не меняется при транспонировании |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

