 |
Главная |
Определение перерезывающих сил и изгибающих моментов
|
из
5.00
|
Министерство науки и образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра ПЛА
Курсовой проект
По дисциплине: Сопротивление материалов
Расчет на изгиб двутавровой балки
Расчет статистически неопределимой плоской рамы
Вариант №14
Студент: Степанов.К.Б Преподаватель: Темников А.И.
Группа: С-21
Факультет: ЛА
НОВОСИБИРСК – 2014
Расчет на изгиб двутавровой балки
УСЛОВИЯ ЗАДАЧИ
 |
Двутавровая стальная балка закреплена на двух шарнирных опорах и нагружена в соответствии с заданной расчётной схемой. Допускаемые напряжения [σ]=160МПа, модуль упругости E=2*105МПа.
Требуется:
1) записать выражения и построить эпюры для изгибающих моментов и перерезывающих сил по силовым участкам;
2) из условия полной проверки на статическую прочность подобрать по ГОСТу требуемый номер двутаврового профиля;
3) с использованием универсального уравнения упругой линии записать выражения для прогибов и углов поворота по силовым участкам;
4) построить эпюры углов поворота (в градусах) и прогибов (в миллиметрах).
 РЕШЕНИЕ ЗАДАЧИ №1
РЕШЕНИЕ ЗАДАЧИ №1
ИСХОДНЫЕ ДАННЫЕ
Двутавровая балка закреплена на двух шарнирных опорах и нагружена в соответствии с заданной расчетной схемой 1.1, как показано на рис. 1.1. Исходные данные и механические характеристики представлены в табл. 1.1.
Исходные данные
| Параметры | Значения параметров |
| М1, кНм | |
| Р1, кН, | |
| Р2, кН, | |
| q, кН/м | |
| a, м | 0,4 |
 , МПа , МПа
| |
| Е, МПа | 2,0*105 |

Определение перерезывающих сил и изгибающих моментов.
1) Определение реакции опор
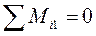
P2*a-P1*2a-M1-P1*4a-q*4a*3a+R7*6a=0
R7=40,33 кН
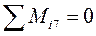
-R1*6a-P2*5a+P1*4a-M1+P1*2a+q*4a*3a=0
R1=8,8 кН
 Проверка:
Проверка: 
R1+P2-2P1-4qa+R7=0
8,8+30-10-4*40*0,4+40,3=0
Построение эпюр внутренних силовых факторов
Участок 1-2 (0≤x≤a)
Qy1-2=R1=8,8 кН
Mz1-2(x)=R1*x
Mz1-2(0)=0 кНм
Mz1-2(a)=17,28 кНм
Участок 2-3 (a≤x≤2a)
Qy2-3(x)=R1+P2-q(x-a)
Qy2-3(a)=48,8 кН
Qy1-2(2a)=30,8 кН
Mz2-3(x)= R1*x+P2(x-a)-q(x-a)2/2
Mz2-3(a)=17,28 кНм
Mz2-3(2a)=41,16 кНм
Участок 3-4 (2a≤x≤3a)
Qy3-4(x)=R1+P2-P1-q(x-a)
Qy3-4(2a)=15,8 кН
Qy3-4(3a)=-2,2 кН
Mz3-4(x)=R1*x+P2*(x-a)-P1*(x-2a)-q(x-a)2/2
Mz3-4(2a)=41,16 кНм
Mz3-4(3a)=45,24 кНм
Участок 4-5 (3a≤x≤4a)
Qy4-5(x)=R1+P2-P1-q(x-a)
Qy4-5(3a)=-2,2 кН
Qy4-5(4a)=-20,2 кН
Mz4-5(x)=R1*x+P2*(x-a)-P1*(x-2a)+M1-q(x-a)2/2
Mz4-5(3a)=65,24 кНм
Mz4-5(4a)=58,52 кНм
Участок 5-6 (4a≤x≤5a)
Qy5-6(x)=R1+P2-P1-P1-q(x-a)
Qy5-6(4a)=-35,2 кН
Qy5-6(5a)=-53,2 кН
Mz5-6(x)=R1*x+P2*(x-a)-P1*(x-2a)+M1-P1*(x-4a)-q(x-a)2/2
 Mz5-6(4a)=58,52 кНм
Mz5-6(4a)=58,52 кНм
Mz5-6(5a)=32 кНм
Участок 6-7 (5a≤x≤6a)
Qy6-7=R1+P2-P1-P1-4qa=-53,2
Mz6-7(x)=R1*x+P2*(x-a)-P1*(x-2a)+M1-P1*(x-4a)-4a*q(x-3a)
Mz6-7(5a)=32 кНм
Mz6-7(6a)=0 Нм
 1.2.3 Расчёт балки на полную статическую прочность при изгибе.
1.2.3 Расчёт балки на полную статическую прочность при изгибе.
1. Номер двутаврового сечения балки определяем из расчёта на прочность по максимальным нормальным напряжениям. В сечении с
Mmax=65,24 кНм
должно выполняться условие  , откуда находим потребный момент
, откуда находим потребный момент
сопротивления балки
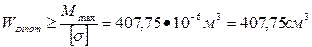
По ГОСТу 8239-72 выбираем ближайший по моменту сопротивления двутавровый профиль №27а с Wz=407 см3 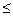 Wzпотр.
Wzпотр.
Геометрические и жесткостные параметры двутаврового профиля:

h=270*10-3 м
b=135*10-3 м
t=10,2*10-3 м
d=6*10-3 м
h2=h-2t=249,6*10-3 м
Jz=5500*10-8 м4
Wz=407*10-6 м3
Szmax=229*10-6м3
2. Выполняем проверку по максимальным напряжениям. Допустим, что в одном из сечений балки действует максимальная перерезывающая сила и максимальный изгибающий момент. Тогда такое сечение проверяется на прочность следующим образом:


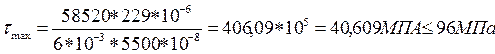
Прочность по максимальным касательным напряжениям обеспечена.
3. Проверяем прочность (по четвёртой теории прочности) точки B поперечного сечения балки, рассматривая наиболее опасные участки:
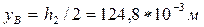 ,
, 
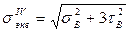
Участок 2-3
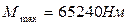 ,
, 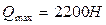





Перенапряжение 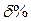 не превышает 10%, поэтому выбранный двутавр №27а может быть оставлен в конструкции балки.
не превышает 10%, поэтому выбранный двутавр №27а может быть оставлен в конструкции балки.
 1.2.4 Определение прогибов и углов поворота балки.
1.2.4 Определение прогибов и углов поворота балки.
Для определения прогибов и углов поворота воспользуемся универсальным уравнением упругой линии, которое для балки с постоянной жесткостью имеет вид:
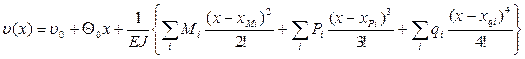

В нашем случае:

Произвольные постоянные 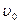 и
и  определяются из граничных условий:
определяются из граничных условий:
 при x=0 и x=6a
при x=0 и x=6a 


|
из
5.00
|
Обсуждение в статье: Определение перерезывающих сил и изгибающих моментов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

