 |
Главная |
Указания по выполнению контрольных работ
|
из
5.00
|
СБОРНИК
ЗАДАНИЙ КОНТРОЛЬНЫХ РАБОТ
Дисциплины: «Алгебра и геометрия», «Математический анализ»
Калининград 2015
ЛИТЕРАТУРА
ОСНОВНАЯ
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Изд. 1-5,-М.,1997.-Т.1,2.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Виницкая Ж.И., Кутузова Т.А., Мозговая Н.К. Математика. Методические указания, образцы выполнения и задания контрольной работы №1 для студентов заочной формы обучения специальностей Бухгалтерский учет, Финансы и кредит. КГТУ, Калининград-2005 .
Альтшуль Б.А. 1. Виницкая Ж.И., Кутузова Т.А., Мозговая Н.К. Высшая математика. Методические указания, образцы выполнения и задания контрольной работы №2 для студентов заочной формы обучения специальностей Бухгалтерский учет, КГТУ, Калининград-1999 .
Альтшуль Б.А., Виницкая Ж.И и др. Высшая математика. Методические указания по выполнению контрольных работ для студентов- заочников общетехнических специальностей Часть 1 ( алгебра и геометрия) КГТУ, Калининград-2000.
Указания по выполнению контрольных работ.
Студент должен выполнять контрольные работы по варианту, номер которого совпадает с последней цифрой его учебного шифра; числа, стоящие в строках, приведенные в таблице, обозначают номера задач, которые он должен решить.
При выполнении и оформлении контрольных работ необходимо соблюдать следующие правила:
1. В начале работы должны быть ясно написаны фамилия студента, его инициалы, шифр, номер контрольной работы.
2. Контрольная работа выполняется в тетради или на листах, обязательно темными чернилами, с полями для замечаний преподавателя.
3. Решения задач контрольной работы располагаются в порядке номеров, указанных в контрольной работе, перед решением задачи должно быть записано полностью ее условие, исходя из данных своего варианта задания. В том случае, когда несколько задач имеют общую формулировку, переписывая условие задачи, следует заменить общие данные конкретными из своего варианта.
4. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов.
Контрольные работы, выполненные с нарушением изложенных правил или выполненные студентом не по своему варианту, возвращаются без проверки.
Получив прорецензированную работу, студент должен исправить в ней все отмеченные ошибки и недочеты. Если работа незачтена, то нерешенные задачи, указанные рецензентом должны быть выполнены заново в той же тетради и возвращены на повторную проверку.
Зачтенные контрольные работы надо предъявить преподавателю на экзамене (зачете).
Задачи для контрольной работы по алгебре и геометрии.
1-10. Даны векторы а(), b(), c(); и
d() в некотором базисе. Показать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе с помощью формул Крамера.
1. a (1;2;3), b (-1;3;2), c(7;-3;5), d(6;10;17).
2. a (4;7;8), b (9;1;3), c(2;-4;1), d(1;-13;-13).
3. a (8;2;3), b (4;6;10), c(3;-2;1), d(7;4;11).
4. a (10;3;1), b (1;4;2), c(3;9;2), d(19;30;7).
5. a (2;4;1), b (1;3;6), c(5;3;1), d(24;20;6).
6. a (1;7;3), b (3;4;2), c(4;8;5), d(7;32;14).
7. a (1;-2;3), b (4;7;2), c(6;4;2), d(14;18;6).
8. a (1;4;3), b (6;8;5), c(3;1;4), d(21;18;33).
9. a (2;7;3), b (3;1;8), c(2;-7;4), d(16;14;27).
10. a (7;2;1), b (4;3;5), c(3;4;-2), d(2;-5;-13).
11-20. Даны координаты вершин пирамиды . Найти
1) длину ребра; 2)угол между ребрами и ; 3) угол между ребром и гранью; 4) площадь грани ;
5) объем пирамиды; 6) уравнения прямой; 7) уравнение плоскости; 8) уравнения высоты, опущенной из вершины на грань. Сделать чертеж.
11. (4;2;5), (0;7;2), (0;2;7), (1;5;0).
12. (4;4;10), (4;10;2), (2;8;4), (9;6;4).
13. (4;6;5), (6;9;4), (2;10;10), (7;5;9).
14. (3;5;4), (8;7;4), (5;10;4), (4;7;8).
15. (10;6;6), (-2;8;2), (6;8;9), (7;10;3).
16. (1;8;2), (5;2;6), (5;7;4), (4;10;9).
17. (6;6;5), (4;9;5), (4;6;11), (6;9;3).
18. (7;2;2), (5;7;7), (5;3;1), (2;3;7).
19. (8;6;4), (10;5;5), (5;6;8), (8;10;7).
20. (7;7;3), (6;5;8), (3;5;8), (8;4;1).
21-30. Составить уравнение прямой, проходящей через центр окружности перпендикулярно одной из асимптот гиперболы 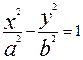 .
.

 .
.

 .
.

 .
.

 .
.
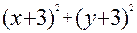
 .
.

 .
.

 .
.

 .
.

 .
.

 .
.
31-40. Дана система линейных уравнений


Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 
39.  40.
40. 
41-50.В треугольнике АВС:
1)Составить уравнения: стороны ВС; высоты из вершины А; медианы из вершины С;
2)Найти площадь треугольника;
3)Найти угол А.
41.  42.
42. 
43.  44.
44. 
45.  46.
46. 
47.  48.
48. 
49.  50.
50. 
Ниже приведена таблица номеров задач, входящих в задания контрольной работы
| Вариант | Номера задач | ||||
Задачи для контрольной работы №1 по математическому анализу.
1-10. Вычислить пределы функций, не пользуясь средствами дифференцирования.










11-21. Найти производные заданных функций.
11. а)  б)
б) 
в)  г)
г)  ;
;
д)  .
.
12. а)  б)
б) 
в)  г)
г)  ;
;
д)  .
.
13. а) 
 ; б)
; б) 
в)  г)
г) 
д) 
14. а)  б)
б) 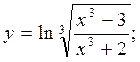
в)  г)
г)  ;
;
д) 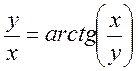 .
.
15. а)  б)
б) 
в)  г)
г)  ;
;
д) 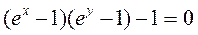
16. а)  б)
б) 
в)  г)
г) 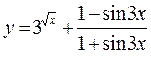 ;
;
д)  .
.
17. а)  б)
б) 
в)  г)
г) 
д)  .
.
18. а)  ; б)
; б) 
в)  ; г)
; г) 
д)  .
.
19. а)  б)
б) 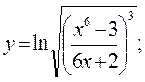
в)  г)
г)  ;
;
д)  .
.
20. а) 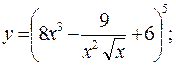 б)
б) 
б)  в)
в) 
д)  .
.
21-30. Найти  и
и  для заданных функций: а)
для заданных функций: а)  ;
;
б)  ;
;  .
.
21. а)  ; б)
; б)  ,
,  .
.
22. а)  ; б)
; б)  ,
,  .
.
23. а)  ; б)
; б)  ,
,  .
.
24. а)  ; б)
; б)  ,
,  .
.
25. а)  ; б)
; б)  ,
,  .
.
26. а) 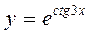 ; б)
; б)  ,
,  .
.
27. а)  ; б)
; б)  ,
, 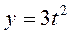 .
.
28. а)  ; б)
; б) 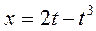 ,
, 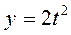 .
.
29. а)  ; б)
; б) 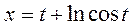 ,
,  .
.
30. а)  ; б)
; б)  ,
,  .
.
31-40. Исследовать методами дифференциального исчисления функцию  и, используя результаты исследования, построить график.
и, используя результаты исследования, построить график.
31.  . 32.
. 32.  . 33.
. 33.  . 34.
. 34.  .
.
35.  . 36.
. 36.  . 37.
. 37.  . 38.
. 38.  .
.
39. 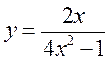 . 40.
. 40.  .
.
41-50. Найти наименьшее и наибольшее значения функции  в замкнутой области D, заданной системой неравенств.
в замкнутой области D, заданной системой неравенств.
Сделать чертёж.
41.  ;
;  .
.
42.  ;
;  .
.
43.  ;
;  .
.
44.  ;
;  .
.
45.  ;
; 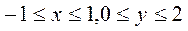 .
.
46.  ;
;  .
.
47.  ;
;  .
.
48.  ;
; 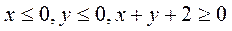 .
.
49. 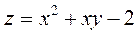 ;
;  .
.
50.  ;
; 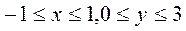 .
.
Ниже приведена таблица номеров задач, входящих в задания контрольной работы.
Контрольная работа №1
| Вариант | Номера задач | ||||
Задачи для контрольной работы №2 по математическому анализу.
51-60. Найти неопределенные интегралы. Правильность результатов проверить дифференцированием.
51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61-70. Вычислить определенный интеграл.
61.

| 62.
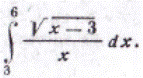
|
63.

| 64.

|
65.

| 66.

|
67.

| 68.
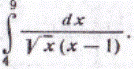
|
69.

| 70.
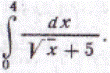
|
71-80. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области.
71.

72.

73.

74.

75.

76.

77.

78.

79.

80.

81-90. Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости.
81.
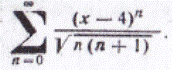
| 82.

|
83.
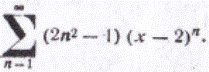
| 84.

|
85.
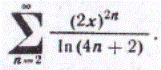
| 86.
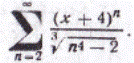
|
87.

| 88.

|
89.

| 90.

|
91-100. Найти общее решение дифференциального уравнения первого порядка и частное решение, удовлетворяющее начальному условию  при
при  .
.
91.

92.

93.

94.

95.

96.

97.
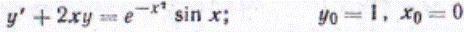
98.

99.

100.

101-110. Найти общее решение дифференциального уравнения порядка выше первого и частное решение, удовлетворяющее начальным условиям.
101.

102.
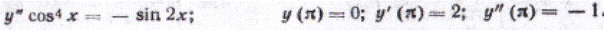
103.

104.

105.
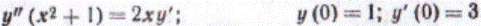
106.

107.
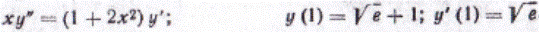
108.

109.

110.

111-120. Найти общее решение линейного дифференциального уравнения с постоянными коэффициентами и частное решение, удовлетворяющее начальным условиям.
111.


112.
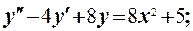

113.


114.


115.
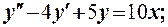

116.

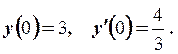
117.


118.


119.

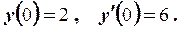
120.


121-130. Найти все значения корня из комплексного числа.
121 
| 122 
| 123 
|
124 
| 125 
| 126 
|
127 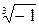
| 128 
| 129 
|
130 
|
Ниже приведена таблица номеров задач, входящих в задания контрольной работы.
Контрольная работа №2
| Вариант | Номера задач | |||||||
|
из
5.00
|
Обсуждение в статье: Указания по выполнению контрольных работ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

