Уравнение парной линейной регрессии

Если зависимость между результатом и фактором установлена, то ее целесообразно представить математической функцией 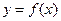. При выборе типа функции (линейная или нелинейная) руководствуются характером расположения точек на поле корреляции, а также содержанием изучаемой связи, которая наилучшим образом соответствует исходным данным, иначе говоря, обеспечивает наилучшую аппроксимацию поля корреляции.

Когда влияние изменения фактора на результат постоянно, используют линейную функцию, в других случаях необходимо применять нелинейные функции.

Математическое описание зависимости в среднем изменений результативного признака 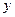от фактора 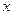называется уравнением парной регрессии.

Парная линейная регрессия имеет вид

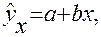
где 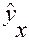- среднее значение результативного признака при определенном значении факторного признака ;

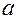- свободный член уравнения регрессии; - коэффициент регрессии.

Построение регрессионной модели включает следующие основные этапы:

- определение цели исследования;

- оценка однородности исходных данных;

- выбор формы связи между результатом и отобранными факторами;

- определение параметров модели;

- оценка тесноты связи;

- определение показателей эластичности;

- проверка качества построенной модели.

 

Вернемся к рассматриваемому примеру 1.1 и построим
уравнение парной линейной регрессии.

Вначале оценим однородность исходных данных,
для чего рассчитаем коэффициент вариации (см. гл. 6):

 

= 12,99/91 * 100% = 16,04%.

Значение коэффициента вариации менее 30%, что говорит об однородности исходных данных, а следовательно, о возможности построения уравнения регрессии.

Найдем параметры 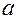и парной линейной регрессии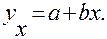

Для этого используем метод наименьших квадратов (МНК). Исходное условие МНК:

 

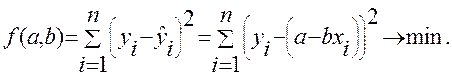
Нужно подобрать такую прямую 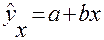, которая отражает минимальность суммы квадратов отклонений фактических значений результативной переменной от ее теоретических значений, получаемых на основе уравнения регрессии.

Для этого воспользуемся системой нормальных уравнений МНК для прямой:

 

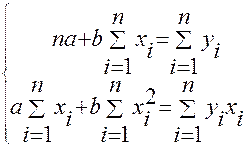
Решая эту систему, можно получить формулы для определения параметров 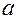и :

Используя расчетные данные табл. 1.2, получаем

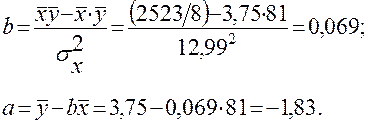
Теперь можно записать уравнение парной регрессии:

 

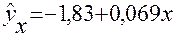
Параметр 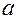выполняет роль доводки до соотношения между средними признакам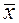и и 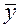, никакого экономического смысла в него не вкладывается. Параметр (коэффициент регрессии) показывает, что в среднем с ростом накопленных за семестр баллов на одну единицу оценка растет на 0,069 балла.

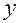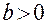Направление связи между признаками и определяет знак коэффициента регрессии . В нашем примере , т.е. связь является прямой. Если 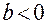- связь является обратной, т.е. с ростом значений фактора значения результата 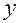уменьшаются.

В отличие от коэффициента корреляции коэффициент регрессии является асимметричной характеристикой связи: он характеризует не просто связь между переменными, а зависимость изменения 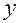от , но не наоборот.

Когда единицы измерения исследуемых показателей различаются, для оценки влияния факторов на результативный признак вычисляют коэффициенты эластичности.

В нашем примере максимально возможное число баллов, которое можно получить на экзамене, равно 5, а максимально накопленное за семестр число баллов равно 100.

Средний коэффициент эластичности для парной линейной регрессии рассчитывается по формуле

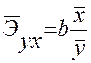
Он показывает, на сколько процентов изменяется результативный признак 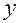при изменении факторного признака на 1 % от своего среднего значения.

В нашем примере

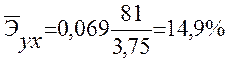
Это означает, что при увеличении накопленных за семестр баллов на 1% оценка за экзамен увеличивается примерно на 15%.

По уравнению 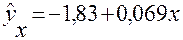рассчитаем ожидаемые (теоретические) значения экзаменационной оценки для каждого студента . Результаты представлены в табл. 8.3. Значения подтверждают, что найденная линия регрессии является наилучшей для аппроксимации исходных данных.

Отклонения фактических оценок от теоретических невелики. Для оценки этих отклонений рассчитывают ошибку аппроксимации. Средняя относительная ошибка аппроксимации определяется по формуле:

 

 

Найдем ошибку аппроксимации для нашего примера.

Для этого составим расчетную таблицу (табл. 1.3).

Таблица 1.3

 

В нашем примере 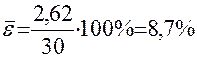, что говорит о хорошем качестве уравнения регрессии, поскольку ошибка аппроксимации в пределах

6 – 10% свидетельствует о хорошем соответствии модели исходным данным.

В последней графе табл. 1.3 показаны квадраты отклонений фактических значений от расчетных .

Сумма 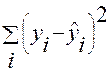является составляющей общей колеблемости 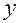, которая в регрессионном анализе представлена следующим образом:

 

где 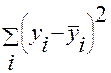- общая колеблемость;

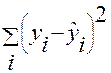- остаточная колеблемость;

- колеблемость 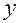, объясненная уравнением регрессии.

Это разложение вариации зависимой переменной лежит в основе оценки качества полученного уравнения регрессии: чем большая часть вариации 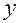объясняется регрессией, тем лучше качество регрессии, т.е. правильно выбран тип функции для описания зависимости 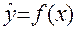, правильно выделена объясняющая переменная (признак-фактор) .

Отношение объясненной вариации к общей вариации
позволяет найти коэффициент детерминации

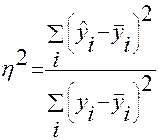
Этот коэффициент определяет степень детерминации
регрессией вариации .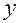

 

Корень квадратный из коэффициента детерминации называется теоретическим корреляционным отношением, он определяет тесноту связи между результативным и факторным признаками при линейной и нелинейной зависимости. Теоретическое корреляционное отношение изменяется от 0 до 1. Чем ближе его значение к 1, тем связь между признаками теснее.

В нашем примере = 7,5 (табл.1.2) – 1,094 (табл.1.3) = 6,406.

Отсюда , или 85%, что совпадает с ранее полученным значением коэффициента детерминации.

В случае высокой детерминации 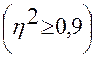уравнение регрессии может использоваться для прогнозирования зависимой переменной. В этом случае можно предсказать ожидаемое значение 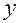по уравнению регрессии на основе ожидаемого значения .

В нашем примере уравнение регрессии позволяет определить ожидаемую экзаменационную оценку на основе суммы накопленных за семестр текущих баллов.

Выполнить регрессионный анализ, можно воспользовавшись ПК и пакетами прикладных программ Excel, EViews, Statgraphics, Statistica и т.д.

Рассмотрим построение парной линейной регрессии с помощью Мiсrоsоft Office Exce12007.

 

Для этого надо произвести следующие действия.

1.Выбрать Данные ―> Анализ данных ―> Регрессия.

2.В диалоговом окне Регрессиясделать следующее:

- ввести в окне Редактирование Входной интервал Yдиапазон зависимой переменной;

- ввести в окне Редактирование Входной интервал Хдиапазон факторной переменной; .

- установить флажок Метки, если первая строка содержит название столбцов;

- установить флажок Константа-ноль, если в уравнении регрессии отсутствует свободный член ;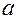

- ввести в окне Редактирование Выходной интервал
номер свободной ячейки на рабочем листе;

- нажать кнопку ОК.

 

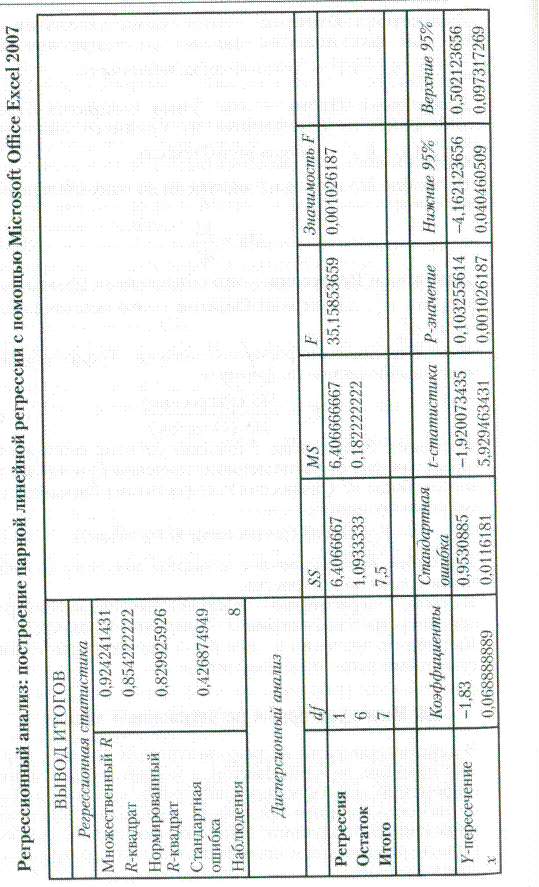
В табл. 1.4 представлены результаты расчета с помощью

Мiсrоsоft Office Excel:

 

а) Регрессионная статистика:

- множественный R - коэффициент корреляции ;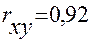

- R-квадрат - коэффициент детерминации ;

- наблюдения - число наблюдений n=8;

б) Дисперсионный анализ:

- столбец df - число степеней свободы.

Для строки Регрессия число степеней свободы определяется количеством параметров тв уравнении регрессии: df_ф = т -1.

В нашем примере два параметра: df_ф = 2 - 1 = 1.

Для строки Остаток (остаточная вариация) число степе-
ней свободы равно: df_oc= n - т.

В примере: df_oc = 8 - 2 = 6.

Для строки Итого (общая вариация) число степеней свободы равно:

df_y = df_ф + df_oc = n - 1.

В примере: df_y= 8 - 1 = 7.

Столбец SS содержит суммы квадратов отклонении.

Для строки Регрессия - это сумма квадратов отклонений теоретических данных от среднего значения:

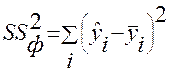- колеблемость 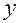, объясненная уравнением регрессии.

Для строки Остаток - это сумма квадратов отклонений фактических данных от теоретических:

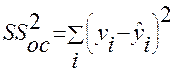- остаточная колеблемость.

 

Для строки Итого - это сумма квадратов отклонений фактических данных от среднего значения:

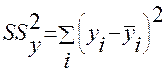- общая колеблемость.

В столбце MSпоказаны дисперсии на одну степень свободы:

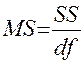
Для строки Регрессия - это объясненная (факторная) дисперсия 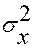, для строки Остаток - это остаточная дисперсия .

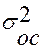В столбце показано расчетное значение F-критерия Фишера 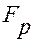, вычисляемое по формуле

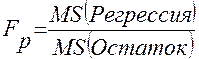
В столбце Значимость F показан уровень значимости, который зависит от вычисленного значения 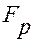и числа степеней свободы df (регрессия);

df (остаток) определяется с помощью функции

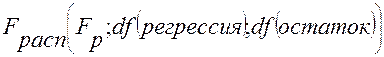
В столбце Коэффициенты показаны значения коэффициентов уравнения регрессии.

В строке Y-пересечение - показано значение параметра а уравнения регрессии, в строке х - значение параметра b.

Как видим, значения в табл. 1.4 совпадают с расчетами,
полученными ранее на калькуляторе.

 

 

Таблица 1.4