 |
Главная |
СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ
|
из
5.00
|
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (филиал)
Государственного образовательного учреждения
Высшего профессионального образования
«МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ
(государственный университет)» (г. Лесной)
 |
| кафедра ТЕХНИЧЕСКИХ СИСТЕМ КОНТРОЛЯ И УПРАВЛЕНИЯ |

СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ
ТРИГГЕРЫ
учебно-методическое описание лабораторной работы по курсу:
«Вычислительные машины, сети и системы»
для студентов, обучающихся по специальности 220201
«Управление и информатика в технических системах»
Составила: ст. преподаватель
Н.А. Рябкова
Утверждено
на заседании кафедры ТСКУ
«__» сентября 2005 г.
Протокол №__
2005 г.
Лабораторная работа №1
СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ
ЦЕЛЬ РАБОТЫ: Изучение интегральных микросхем И - НЕ.
Синтез логических схем.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В цифровых вычислительных машинах вся информация, необходимая для реализации вычислительного процесса, вводится в виде набора дискретных сигналов. Набор входных сигналов преобразуется устройствами (цепями) машины в соответствии с программой вычислительного процесса. Так, например, вычислительные цепи преобразуют совокупность сигналов, поданных на их вход в соответствии с реализуемой вычислительной операцией. Управляющие цепи преобразуют входные сигналы в совокупность выходных сигналов, управляющих передачей информации из одного устройства машины в другое и т.д.
Рассмотрим некоторое устройство (рис.1) с n-входами и m-выходами, на каждый вход которого может быть подан произвольный символ из конечного алфавита X = (а0, а1, ... аk).
X
| i n | j m | Y |
Рис.1
Совокупность символов, поданных на вход устройства, образует входные слова X (X0, X1, X2 ... Xn ). На выходе устройства появляются выходные слова Y (Y0, Y1, Y2 ... Ym ) из символов выходного алфавита Y = (b0, b1, ... bn).
Элементарный такт работы устройства состоит в том, что при подаче на вход устройства входного слова X, на выходе появляется выходное слово Y.
Логической функцией (ЛФ) называется функция, дающая однозначное отображение (соответствие) X®Y (X в Y).
Логическая функция называется k - значной, если входной и выходной алфавиты состоят из k - символов.
Обычно каждый из символов в наборе может принимать одно из двух возможных значений: 1 или 0, отождествляемых с логическими понятиями -истина (1) и ложь (0). Символ "1" обозначает наличие сигнала, "0" - отсутствие сигнала.
Логическая функция называется двоичной, если входной и выходной алфавиты состоят из символов 0 и 1, X = (0; 1), Y = (0; 1).
Физическая реализация сигнала может быть различной:
1. Включено (замкнуто) - 1 (0), выключено (разомкнуто) - 0 (1);
2. Ток проходит - 1 (0), ток не проходит - 0 (1);
3. Напряжение высокое - 1 (0), напряжение низкое - 0 (1);
4. Наличие импульса - 1 (0), отсутствие импульса - 0 (1).
Вышеприведенные обозначения произвольны. Для исключения путаницы принято различать положительную и отрицательную логики. В том случае, когда за сигнал единицы принимается сигнал с более положительным уровнем, чем сигнал нуля, то имеет место положительная логика, в противном случае -отрицательная логика (рис.2).
 |
| Положительная логика | U | |||||
| t |

 |
| Отрицательная логика | U | t | |||

Рис.2
Формы представления логических функций
Логические функции могут быть представлены в виде:
1. Таблицы истинности (карт), дающих однозначное соответствие между комбинациями входных и выходных переменных. Существует несколько разновидностей таблиц (карт) истинности, отличающихся расположением и способом записи входных и выходных комбинаций.
2. Алгебраических (буквенных) выражений. Каждая переменная обозначается буквенным символом. Соотношения между переменными функциями обозначаются логическими символами: « + », « × » , « - » (черта над буквенным символом), « Å », « Ú », « Ù », и т. д.
Основные элементарные логические функции
Наибольшее распространение при анализе и синтезе логических устройств получили следующие три основные элементарные логические функции:
1. ОТРИЦАНИЕ (инверсия, «НЕ») логической функции от одной вход- ной переменной - X, которая может принимать значения 0 или 1. Соответствие между входом и выходом задается в виде таблицы:
| Вход | Выход |
| X | Y |
При записи в алгебраической форме отрицание обозначается логическим символом "черта", которая ставится над переменной (функцией).
Y = `X (Y есть не X)
Элемент (см. рис.3), реализующий функцию отрицания, называется инвертором.
 |
Рис.3.
2. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (конъюнкция, «И») для логической функции от двух переменных определяется таблицей:
| X1 | X2 | Y |
Для обозначения операции логического умножения используются
символы « × », « Ù »: Y = X1 × X2 (Y есть X1 и X2)
Y = X1 Ù X2 (Y есть X1 и X2)
Элемент «И», реализующий функцию логического умножения, показан
 |
на рис.4.
Рис.4.
3. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция, «ИЛИ») от двух переменных
определяется таблицей истинности:
| X1 | X2 | Y |
Для обозначения операции логического сложения применяются символы: «+», «Ú»: Y = X1 + X2 = X1Ú X2 (Y есть X1 или X2).
 |
Элемент ИЛИ, реализующий функцию логического сложения, показан на рисунке 5.
Рис.5.
Кроме трех основных логических функций широкое распространение имеют еще шесть (см. таблицу 1) элементарных логических функций.
Таблица 1
| № п/п | Наименование логич. функций | Таблица истинности | Аналитическое выражение | Графическое изображение | |||||||
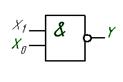
| Отрицание конъюнкции, операция Шеффера, функция И-НЕ | X1 | X0 | Y |
 =
= 
| ||||||

| Отрицание дизъюнкции, операция Пирса, функция ИЛИ-НЕ | X1 | X0 | Y |

| ||||||

| Импликация | X1 | X0 | Y |

| ||||||

| Запрет | X1 | X0 | Y |

| ||||||

| Эквивалентность Равнозначность | X1 | X0 | Y |

| ||||||

| Неравнозначность Сложение по модулю два | X1 | X0 | Y |

| ||||||
Тождества алгебры логики
Основные положения алгебры логики позволяют вывести ряд тождеств, которым подчиняются действия над логическими переменными и функциями.
Таблица 2.
| № | Тождество | Название |

| Переместительный закон | |

| Сочетательный закон | |

| Распределительный закон | |
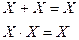
| Правило о повторяющихся переменных | |

| Сложение с единицей | |

| Сложение с нулём | |

| Умножение на единицу | |

| Умножение на нуль | |

| Двойное отрицание | |

| Исключение третьего | |

| Противоречие | |

| Закон инверсии (теорема де Моргана) |
Описание карты истинности (Карно)
Карта истинности представляет собой прямоугольную матрицу, состоящую из N = 2n клеток, где n - число двоичных переменных.
  
| Х | Х1 | Х1 Х2 | ||||||||||||
| Х0 | Х0 | ||||||||||||||
| а) | |||||||||||||||
| б) | |||||||||||||||

| в) | ||||||||||||||
 Х3 Х2 Х3 Х2
| Х4 Х3 Х2 | ||||||||||||||
| Х1 Х0 00 | Х1 Х0 | ||||||||||||||
| г) | |||||||||||||||
| д) | |||||||||||||||
| Номер клетки: | -б) | -в) | -г) | -д) | |||||||||||
| Рис. 6. |
Каждой комбинации логических переменных соответствует клетка с двоичным номером этой комбинации. Единичные значения функции проставляются внутри клетки. Для удобства пользования в карте истинности (карта Карно) столбцы и строки нумеруются в коде Грея.
Номер клетки определяется номером столбца и строки, в пересечении которых находится данная клетка (см. рис.6).
Порядок получения логической функции в минимальной форме с помощью карт истинности
1. Каждую клетку с единицей (нулем) следует включить в какой-либо блок.
2. Каждый выделенный блок должен быть предельно высокого порядка.
3. После подробного рассмотрения различных вариантов выделяется
минимальное количество существенных блоков.
4. Из выделенных блоков составляется функция в дизъюнктивной или
в конъюнктивной форме.
Порядок синтеза логических схем
Синтез заключается в построении логической схемы исходя из физического описания ее работы. Синтез проводится путем последовательного выполнения ряда операций:
1. Составления таблицы (карты) истинности;
2. Получения минимальных логических функций;
3. Построения логической схемы в заданном классе логических элементов.
Последним этапом синтеза является построение логической схемы. Построение логической схемы заключается в последовательной замене элементарных логических функций, из которых состоит реализуемая логическая функция с соответствующими логическими элементами.
Синтез при ограничении по входу
в логических элементах
Максимальное число сигналов, которое можно одновременно подать на вход логического элемента, является одним из основных ограничений, учитываемых при синтезе логических схем.
При синтезе с ограничением по входу число членов логических сумм и произведений не должно превышать числа входов логических элементов. Это условие, как правило, выполняется в минимальных формах, полученных в результате минимизации. Стандартных приемов, позволяющих проводить синтез при ограничении по входу, нет.
Ниже рассматриваются примеры, показывающие частные случаи синтеза с ограничениями.
1.Синтезировать логическую функцию Y = X2 X1 X0 на элементах 2И-НЕ.
Применив к заданной логической функции двойное отрицание, за- пишем ее в виде:  . Логическая схема, реализующая требуемую функцию, представлена на рис. 7.
. Логическая схема, реализующая требуемую функцию, представлена на рис. 7.
 |
Рис. 7.
2. Синтезировать функцию Y =X 2 X 1 X 0 на элементах 2ИЛИ-НЕ.
Приведем функцию к виду:  ,
,
удобному для составления логической схемы следующего рисунка:
 |
Подготовка к выполнению работы
1. Изучить описание лабораторной работы.
2. Ознакомиться с основными параметрами логических элементов И-НЕ серии К155.
3. Составить таблицу истинности для 3Х - входового элемента И-НЕ.
4. Построить логические схемы 4ИЛИ и 4ИЛИ-НЕ на основе элементов
2И-НЕ. Составить таблицу истинности для полученных схем.
5. Синтезировать схему по заданной логической функции (таблица 3).
Примечание: 1. При изображении схем каждый элемент должен соответствовать принятым обозначениям.
2. Студенты, не выполнившие подготовку в полном объёме, к лабораторной работе не допускаются.
Таблица 3
| Вариант | F(a,b,c,d) СДНФ | ||||||
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Исследовать работу 3Х - входового элемента И-НЕ на стенде и
сравнить полученные результаты с таблицей истинности.
2. Исследовать работу элементов 4ИЛИ и 4ИЛИ-НЕ. Полученные
результаты сравнить с таблицей истинности.
3. Исследовать работу схемы, полученной в п.5 домашней подготовки.
4. Минимизировать функцию, заданную преподавателем по карточке.
По полученной функции составить логическую схему, собрать ее
и исследовать на стенде.
5. Составить логическую функцию по заданной преподавателем схе-
ме, минимизировать полученную функцию и построить логическую
схему. Сравнить полученную и исходную схемы, а также соот-
ветствующие им таблицы истинности. Закоммутировать на стенде
схему, соответствующую минимизированной логической функции.
6. Исследовать неизвестную логическую схему. Для этого, сначала
подавая на вход всевозможные комбинации входных сигналов,
составить таблицу истинности. По полученной таблице записать
логическую функцию в СДНФ и СКНФ. Минимизировать эти функ-
ции и составить логические схемы.
Отчёт должен содержать: схемы, таблицы истинности, уравнения и
выводы.
Контрольные вопросы
1. Чем характеризуют быстродействие элементов ЭВМ?
2. Что такое положительная и отрицательная логика?
3. В чем сущность синтеза логических схем?
4. Почему задача синтеза неоднозначна?
5. В чем специфика синтеза многовыходных логических схем?
6. Всегда ли перед минимизацией переключательных функций их не-
обходимо приводить к совершенным формам?
ЛИТЕРАТУРА
Поспелов Д.А. Логические методы анализа и синтеза схем.
М.: Энергия, 1974.
Шило Л.Е. Популярные цифровые микросхемы.
М.: Связь, 1989.
|
из
5.00
|
Обсуждение в статье: СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы





