К О Н Т Р О Л Ь Н А Я Р А Б О Т А

по дисциплине

«МОНИТОРИНГ ОКРУЖАЮЩЕЙ СРЕДЫ»

 

Выполнил: ст.гр. ЭК-21з

Меликян А.С.,

вариант 6

 

Проверил: доц. каф. ПЭОТ

Азаренко Е.И.

 

 

Севастополь

СОДЕРЖАНИЕ

 

Теоретическая часть………………………………………………………………3

1. Аппаратное обеспечение мониторинга. Обработка данных мониторинга………..3

2.Числовые характеристики случайной величины: математическое ожидание, мода, медиана………………………………………………………………………………….10

Практическая часть……………………………………………………………...17

3.Результаты работ……………………………………………………………………..17

Библиография…………………………………………………………………………21

 

 

Теоретическая часть

 

1. Аппаратное обеспечение мониторинга. Обработка данных мониторинга

К настоящему времени в Украине и за рубежом создан большой парк специальной и универсальной контрольно-измерительной и аналитической техники, образцовых средств, технологий проведения анализа, контроля, оценки, обработки информации. В этом плане задача технико-технологического обеспечения экологического мониторинга сводится к выбору оптимального комплекта технических средств наблюдения и контроля из числа серийно выпускаемых различными предприятиями и ведомствами на основе нормативной базы экологического мониторинга.

Результаты экологического мониторинга составляют информационную базу (банк данных) ООС, что позволяет использовать ЭВМ для сбора, хранения, обработки и анализа информации. Информационное обеспечение ООС, в свою очередь, является основой для управления природоохранной деятельностью, проведения ресурсосберегающей политики. Информативность мониторинга во многом зависит от уровня технических средств (оснащенности службы), поэтому при комплектовании парка приборов необходимо руководствоваться всем комплексом нормативов контроля — объемами, периодичностью, требуемой точностью и достоверностью, полнотой. Обязательное условие обеспечения требуемой информативности — использование ЭВМ и средств мониторинга на их основе.

Ведомственная служба экологического мониторинга должна иметь полный комплект необходимых технических средств для контроля всех основных параметров загрязнений окружающей среды. Обычно состав загрязнителей воздуха, воды, почв достаточно точно прогнозируется (оксиды азота, углеводороды и др.), поэтому задача экологического контроля сводится к количественному определению концентраций известных загрязнений. Для этого ведомственные службы экологического контроля достаточно оснастить комплексными передвижными лабораториями анализа качества воздуха, воды, почв.

Организации экологической службы, ее техническому оснащению для контроля какой-либо определенной территории с находящимися на ней источниками техногенеза должны предшествовать научно-исследовательские работы, необходимые для исследования и прогнозирования возможных загрязнений (по составу и объемным концентрациям). Результаты исследований служат основанием для укомплектования контрольных служб техническими средствами измерений и анализа состава и концентраций загрязнителей.

Инспекционные службы применяют разные методы и средства экологического контроля. Все они равноправны по критериям информативности, точности и достоверности.

Технические средства получения и обработки информации

Общая структура аппаратных средств сети наземных измерений в системе экологического мониторинга включает:

1. Для низового уровня мониторинговой сети:

· стационарные посты по воздуху и воде;

· передвижные и стационарные лаборатории по состоянию атмосферы, воды, почвы, снега;

· передвижные станции контроля выбросов и сбросов;

· инспекционные службы;

· службы получения данных от населения.

Число стационарных и передвижных станций и постов определяется в результате проведения исследований, расчётов на имеющихся моделях конкретной природно-технической геосистемы (или природно-территориального комплекса), а также на основании накопленного опыта наблюдения за окружающей средой.

2. Для среднего уровня сети:

· центры сбора и обработки информации, полученной в низовых сетях, отличающиеся друг от друга спецификой и сложностью решаемых задач.

3. Для высшего уровня сети:

· пользователи информации, полученной в центрах ее сбора и обработки.

Непосредственными пользователями данных являются инспектора по охране окружающей среды.

К числу основных составляющих сети мониторинга относятся датчики и анализаторы; устройства загрузки данных; устройства передачи данных и др.

В иерархически построенной сети наземных измерений вычислительные средства обработки информации используются практически на всех уровнях сети. В стационарных и передвижных постах загрузчик данных не только управляет работой анализаторов, но и производит первичную обработку собранных данных. В локальных и центральных вычислительных центрах вычисляются по моделям уровни загрязнения среды по основным и дополнительным ингредиентам, строятся карты изолиний, рассчитываются прогнозы, вычисляются вероятные источники загрязнений и т. п.

Вычислительный центр сети мониторинга загрязнений выполняет следующие функции:

· управление работой сети наземных измерений в оперативном, штормовом режимах и режиме проверки работоспособности;

· сбор информации от стационарных постов и передвижных лабораторий контроля загрязнений;

· ведение банков данных оперативного и долговременного хранения информации с обеспечением надежности хранения информации и защиты от несанкционированного доступа;

· обработка информации для получения общей картины загрязнений для вычисления прогнозов, интегральных оценок экологического состояния среды и др.;

· подготовка и выдача информации о загрязнениях в плановом порядке в виде сводных таблиц, картографического материала и т. п.;

· передача информации в автоматическом режиме в главный вычислительный центр.

Сеть передачи данных наземных измерений со станций экологического мониторинга решает следующие задачи:

· регулярная (один раз в 10 мин, 30 мин, 1 ч и т. п.) передача данных измерений от стационарных постов и передвижных лабораторий;

· передача данных, поступающих от населения о тревожных и аварийных ситуациях;

· передача данных по каналам связи от вычислительного центра пользователям информации (исполнительной власти, населению и т. п.).

Данные, передаваемые от стационарных постов и передвижных лабораторий, невелики по объему (сотни байт), но передаются достаточно часто. Скорость передачи данных невелика — сотни бит в секунду. Требования к надежности передаваемых данных не предельно жесткие, так как протекающие процессы в атмосфере и воде имеют скорость распространения десятки минут, часы.

Данные от вычислительного центра пользователям должны передаваться 1—2 раза в сутки, объем их достаточно велик (единицы и десятки килобайт). Поэтому скорость передачи и требования к надежности передачи данных должны быть достаточно высоки.

Информационное обеспечение системы комплексного экологического мониторинга должно содержать:

· упорядоченную структуру информационных потоков (входных, внутренних, выходных);

· инфраструктуру собственно информационной базы данных;

· методики сбора данных от стационарных и передвижных постов;

· методики передачи данных, полученных от постов различного уровня, включая лидары;

· методики обработки данных и расчета интегральных показателей состояния окружающей среды;

· методики определения источников выбросов;

· структуру пользовательских организаций сети и эксплуатационных служб.

Программное обеспечение сети комплексного экологического мониторинга должно включать:

· развитые операционные системы;

· стандартные базы данных;

· картографическое и графопостроительное обеспечение;

· мониторы для управления сбором данных;

Базой данных называют совокупность хранимых операционных данных, используемых прикладными системами некоторого потребителя. Основополагающим при проектировании или выборе структуры базы данных является модель представления данных.

По способу организации баз данных различают реляционные, иерархические и сетевые базы данных.

Реляционные базы данных строятся на основе реляционной модели данных, использующей математическое понятие теоретико-множественного отношения. База данных при этом представляется в виде совокупности таблиц.

Иерархические базы данных строятся на основе иерархической модели данных, в которой данные имеют структуру простого дерева. База данных представляется при этом в виде совокупности деревьев.

Сетевые базы данных строятся на основе сетевой модели данных, в которой данные имеют структуру ориентированного графа. База данных представляется ориентированной сетью.

Выбор конкретной базы данных зависит от характера выполняемых задач. В соответствии с общей структурой сети наземных измерений должны быть созданы следующие основные базы данных: по воздуху, выбросам и отходам, водным объектам, картографии и др. Большинство из них целесообразно строить как реляционные. В то же время, скажем, для картографических систем могут быть использованы базы данных иерархического типа.

Управление в структуре экологического мониторинга

Изучение сущности современных экологических процессов, попытки регулирования природного и природно-техногенного равновесия не могут обойтись без научного управления системами различного масштаба. Схема управления в применении к экологическим системам при анализе её содержательности переходит в разряд наисложнейших в настоящее время, человеческое общество не обладает возможностями, чтобы решать полностью задачи экологического управления. Подэкологическим управлением понимается сознательная деятельность по регулированию экосферы в соответствии с практическими целями человеческого общества на основе познанных объективных экологических закономерностей естественного или техногенного характера.

Экологическое управление осуществляется на базе целевых функций с учетом предыдущих и текущих показателей экосистемы, модельных прогностических параметров с учетом планирования организационно-технических природоохранных мероприятий.

В целом экологическая мониторинговая система решает одновременно две задачи: познания и управления, причем первая ставится с расчетом на переход ко второй. Данные наблюдения и контроля служат и базой для получения новых знаний и обоснованием к планированию управления объектом. Чем меньше известно об объекте, тем более совершенным должен быть датчик с целью извлечения максимальной информации об объекте контроля и управления.

Достичь экономически эффективного регулирования и управления качеством природной среды при самых строгих нормах природопользования возможно решением следующих вопросов:

· какое качество природной среды в комплексных и единичных показателях будет приниматься за «нормальное» и «высокое»;

· к какому уровню качества природной среды следует стремиться при восстановительной природоохранной деятельности с учетом экологической и экономической точек зрения;

· какими критериями надо руководствоваться в том или ином случае при ответе на предыдущий вопрос;

· проведение каких мероприятий необходимо для уменьшения, снижения или полной компенсации вредных техногенных воздействий, снижения или полной ликвидации экологического ущерба, достижения нового, более высокого уровня качества природной среды;

· какова эффективность и полезность природоохранных, восстановительных или компенсационных действий на длительных временных интервалах (долговременный экологический прогноз);

· как определять приоритетность действий при столкновении экономических и экологических интересов.[1]

2. Числовые характеристики случайных величин

Математическое ожидание. Математическим ожиданием дискретной случайной величины Х, принимающей конечное число значений х_i с вероятностями р_i , называется сумма:

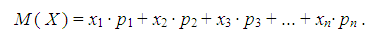(1а)

Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):

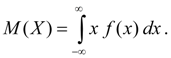(1б)

Несобственный интеграл (1б) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М ( Х) не существует). Математическое ожидание характеризует среднее значение случайной величины Х. Его размерность совпадает с размерностью случайной величины.

Свойства математического ожидания:

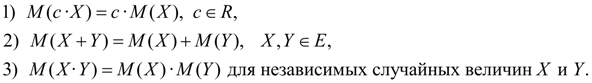(2)

 

Дисперсия. Дисперсией случайной величины Х называется число:

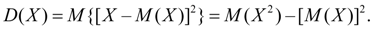(3)

Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (3) и математического ожидания (1а) для дискретной случайной величины и (1б) для непрерывной случайной величины получим аналогичные выражения для дисперсии:

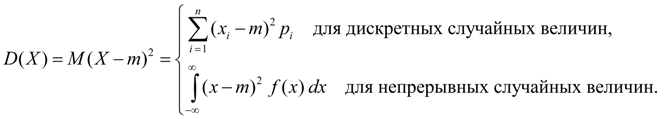(4)

Здесь m = М ( Х ).

Свойства дисперсии:

(5)

Среднее квадратичное отклонение:

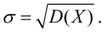(6)

Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.

Моменты распределения.Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х₀ называется математическое ожидание М ( Х – х₀)k . Моменты относительно начала координат х = 0 называются начальными моментамии обозначаются:

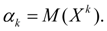(7)

Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:

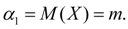(8)

Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:

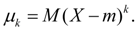(9)

Из (2) следует, что центральный момент первого порядка всегда равен нулю:

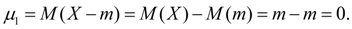(10)

Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С).
Теперь очевидно, что дисперсия – это центральный момент второго порядка:

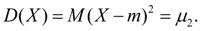(11)

Асимметрия.Центральный момент третьего порядка:

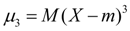(12)

служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии:

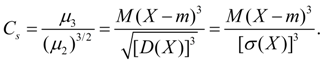(13)

Знак коэффициента асимметрии (13) указывает на правостороннюю или левостороннюю асимметрию (рис. 1).

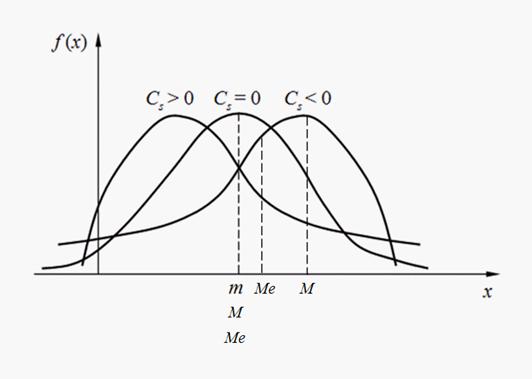
Рис. 1. Виды асимметрии распределений.

 

Эксцесс. Центральный момент четвертого порядка:

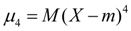(14)

служит для оценки так называемого эксцесса, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения 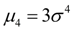, то в качестве эксцесса принимается величина:

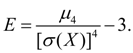(15)

На рис. 2 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

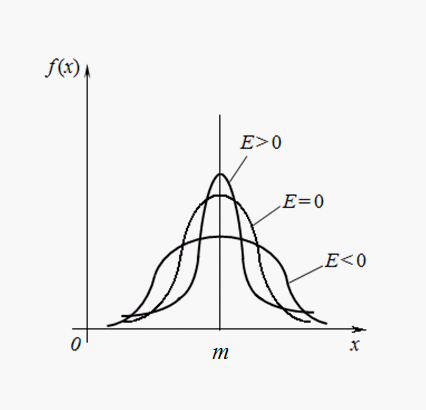
Рис. 2. Кривые распределения с различной степенью крутости (эксцессом).

Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.

Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величины называется ее значение, при котором плотность вероятности максимальна (рис. 1). Если кривая распределения имеет один максимум, то распределение называется унимодальным. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.

Медианаслучайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме. Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 1). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.[2]

 

 

Практическая часть

3. Результаты работ

 

> #Расчет моментов экспериментального распределения.

> restart;

> #Обращение к библиотеке

> with(stats);

 

> #Ввод исходной статистической информации по варианту

> X:=[0.2618,0.5236,0.7854,1.0472,1.3090,1.5708,1.8326,2.0944,2.3562,2.6180,2.8798,3.1416,3.4034,3.6652,3.9270,4.1888,4.4506,4.7124, 4.9742,5.2360,5.4978,5.7596,6.0214,6.2832];

> Y:=[5.60,8.47,11.00,13.53,16.40,19.70,23.17,26.47,29.42,32.13,34.83,37.70,40.75,43.87,47.00,50.13,53.25,56.30,59.17,61.87,64.58,67.53,70.83,74.30];

> #Ввод объема выборки

> n:=24;

> #Расчет математического ожидания

> Mx:=describe[moment[1]](X);

> My:=describe[moment[1]](Y);

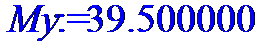
> #Расчет дисперсии

> Dx:=describe[moment[2,Mx]](X);

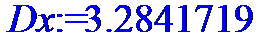
> Dy:=describe[moment[2,My]](Y);

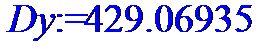
> #Расчет среднего квадратического отклонения

> Sx:=(Dx*n/(n-1))^0.5;

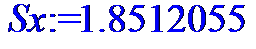
> Sy:=(Dy*n/(n-1))^0.5;

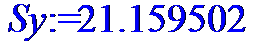
> #Расчет третьего центрального момента

> M3x:=describe[moment[3,Mx]](X);

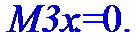
> M3y:=describe[moment[3,My]](Y);

> #Расчет скошенности

> Sk:=M3x/Sx^3;

> Sk:=M3y/Sy^3;

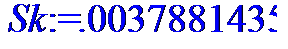
> #Расчет четвертого центрального момента

> M4x:=describe[moment[4,Mx]](X);

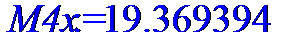
> M4y:=describe[moment[4,My]](Y);

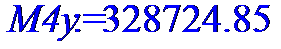
> #Расчет эксцесса

> Ex:=(M4x/Sx^4)-3;

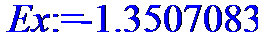
> Ey:=(M4y/Sy^4)-3;

> #Расчет смешанного момента

> for i to n do Z[i]:=X[i]*Y[i]od;

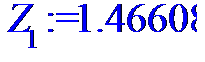
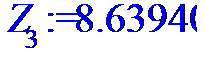
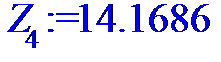
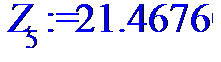
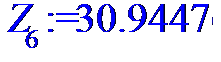
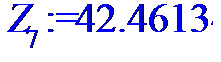
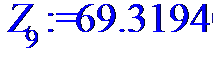
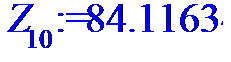
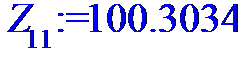
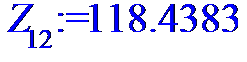
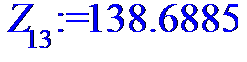
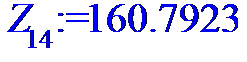
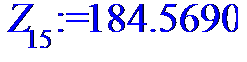
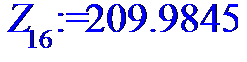
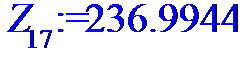
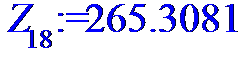
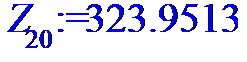
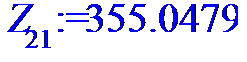
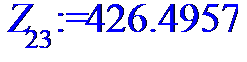
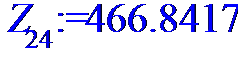
> #Ввод смешанного момента для расчета

> Z:=[Z[1],Z[2],Z[3],Z[4],Z[5],Z[6],Z[7],Z[8],Z[9],Z[10],Z[11],Z[12],Z[13],Z[14],Z[15],Z[16],Z[17],Z[18],Z[19],Z[20],Z[21],Z[22],Z[23],Z[24]];

> #Расчет среднего смешанного момента

> MZ:=describe[moment[1]](Z);

> #Расчет коэффициент корреляции

> r:=(MZ-Mx*My)/(Sx*Sy);

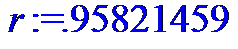
> if abs(r)>0.65 then r:=strong; else r:=iow;fi;

> #Построение графика

> plot([[X[1],Y[1]],[X[2],Y[2]],[X[3],Y[3]],[X[4],Y[4]],[X[5],Y[5]],[X[6],Y[6]],[X[7],Y[7]],[X[8],Y[8]],[X[9],Y[9]],[X[10],Y[10]],[X[11],Y[11]],[X[12],Y[12]],[X[13],Y[13]],[X[14],Y[14]],[X[15],Y[15]],[X[16],Y[16]],[X[17],Y[17]],[X[18],Y[18]],[X[19],Y[19]],[X[20],Y[20]],[X[21],Y[21]],[X[22],Y[22]],[X[23],Y[23]],[X[24],Y[24]]],x=0..7,style=[point]);

>

 

 

Вывод: в результате проведенных расчетов определены:

1.Матиматическое ожидание изучаемой случайной величины (его статистическая оценка)

М_х=3.2725

2.Статистическая оценка дисперсии

D_x=3.2842

3.Скошенность распределения

S_k=0

4.Эксцесс распределения

E_x=1.3507

Библиография

1. М.А. Пашкевич, В.Ф. Шуйский; Санкт-Петербургский государственный горный институт.– СПб, 2002.[1]

2. Е.И.Хлебосолов, О.А.Хлебосолова, Ю.А.Кушель, О.А.Макарова. Методы системного экологического мониторинга. Ряз. обл. ин-т развития образования. - Рязань, 2000. -70 с.[2]