 |
Главная |
Синтез алгоритмов и схем оптимальных приемников
|
из
5.00
|
Международная образовательная корпорация
Факультет Прикладных Наук
Реферат
на тему«Синтез алгоритмов и схем оптимальных приемников»
По дисциплине«Теория электрической связи»
Выполнила:студент группы
ФПН-РЭиТ(з)-4С*
Джумагельдин Д
Проверила:Глухова Н.В
Алматы, 2015
Содержание
І Введение
ІІ Основная часть
1. Синтез алгоритмов
2. Схемы оптимальных приемников
2.1 Структурная схема оптимального приемника
ІІІ Заключение
ІV Список использованной литературы
Введение
В настоящее время в связи с ростом числа совместно работающих радиотехнических систем различного назначения много внимания уделяется вопросам синтеза оптимальных приемников обнаружения полезных сигналов на фоне активных и пассивных мешающих сигналов и помех. Активные помехи представляют собой излучаемые зондирующие сигналы других РЛС, мощные сигналы связных передающих связных станций, запросные сигналы бортовых и наземных радионавигационных систем. Пассивными помехами служат отраженные радиосигналы от подстилающей поверхности, метеообразований (зоны облачности, тумана), искусственных предметов возвышающихся над местностью. На практике амплитуды и фазы сигналов в результате отражения от целей, объектов сложной формы и подстилающей поверхности, многолучевого распространения радиоволн, прохождения через области гидрометеоров могут иметь распределение отличное от нормального.
В литературе описано достаточно методов и способов построения оптимальных приемников , при воздействии на их входы различных мешающих сигналов и помех, которые, однако, имеют сложную техническую реализацию.
Синтез алгоритмов и схем оптимальных приемников
Алгоритмы приемников полезных сигналов, полученные при следующих допущениях:
1) негауссовская помеха предполагается заградительной (или прицельно – заградительной), т.е. ширина энергетического спектра помехи 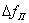 намного превосходит ширину спектра анализируемого сигнала
намного превосходит ширину спектра анализируемого сигнала  :
:
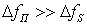 . (1)
. (1)
Причем спектр частот помехи предполагается достаточно равномерным хотя бы в полосе частот полезного сигнала (так называемая негауссовая помеха типа белого шума). Для негауссовой помехи типа белого шума функционал вероятности 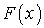 как показано в [3], равен:
как показано в [3], равен:
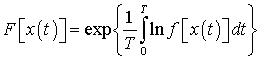 , (2)
, (2)
где 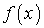 - одномерная плотность вероятности негауссовской помехи
- одномерная плотность вероятности негауссовской помехи 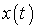 , а
, а 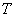 - интервал наблюдения, равный длительности сигнала. В случае белого гауссовского шума из выражения (2) вытекает известная из литературы формула для функционала вероятности белого гауссовского процесса, что приводит к корреляционному приемнику, эквивалентному согласованному фильтру (СФ);
- интервал наблюдения, равный длительности сигнала. В случае белого гауссовского шума из выражения (2) вытекает известная из литературы формула для функционала вероятности белого гауссовского процесса, что приводит к корреляционному приемнику, эквивалентному согласованному фильтру (СФ);
2) мощность сигнала 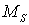 значительно меньше мощности помехи
значительно меньше мощности помехи 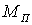 :
:
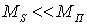 . (3)
. (3)
Это условие всегда выполняется при воздействии мощных помех на приемники связных или радиолокационных систем. Кроме того, оптимизация систем всегда целесообразна для слабых сигналов;
3) на вход приемники системы обнаружения поступает смесь полностью известного сигнала 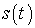 и негауссовой помехи
и негауссовой помехи 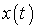 :
:
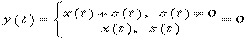 (4)
(4)
Используя выражение (2), нетрудно записать отношение правдоподобия 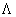 , и, с учетом условий (3,4) получить алгоритм обнаружения
, и, с учетом условий (3,4) получить алгоритм обнаружения 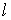 оптимального приемника:
оптимального приемника:
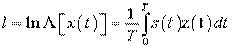 , (5)
, (5)
и для вынесения решения о наличии (или отсутствии) сигнала во входной смеси случайная величина 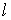 должна сравниваться с порогом
должна сравниваться с порогом 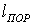 , величина которого выбирается из обеспечения требуемого уровня ложных тревог. В формуле (5)
, величина которого выбирается из обеспечения требуемого уровня ложных тревог. В формуле (5) 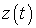 есть случайный процесс на выходе нелинейного четырехполюсника (НЧ) [3], амплитудная характеристика которого равна:
есть случайный процесс на выходе нелинейного четырехполюсника (НЧ) [3], амплитудная характеристика которого равна:
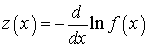 . (6)
. (6)
Анализ алгоритма (5) показывает, что оптимальный приемник после усилителя промежуточной частоты (УПЧ) должен состоять из НЧ с амплитудной характеристикой (6), и, как показано в [4], коррелятора или оптимального линейного фильтра (ОФ), частотная характеристика которого т сопряжена со спектром сигнала 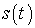 . Далее следует пороговое устройство (ПУ).
. Далее следует пороговое устройство (ПУ).

Рис.1 Структурная схема оптимального приемника.
Нетрудно привести физическое толкование тому факту, что ОФ сопряжен со спектром входного сигнала, а не со спектром сигнала на выходе НЧ. Действительно, т.к. сигнал слабый, то НЧ для сигнала линеаризуется, и сигнал на выход НЧ в первом приближении проходит практически без искажений. Спектр помехи остается не менее широкополосным на выходе НЧ (и, конечно, более широким, чем спектр сигнала).
В общей форме сигнал можно записать в виде:
 , (7)
, (7)
где 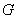 и
и 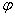 есть случайная амплитуда и неизвестная начальная фаза распределений, которые, соответственно, релеевское и равномерное (равновероятное):
есть случайная амплитуда и неизвестная начальная фаза распределений, которые, соответственно, релеевское и равномерное (равновероятное):
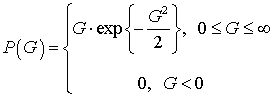 (8)
(8)
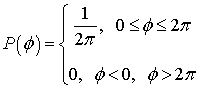 , (9)
, (9)
а 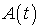 и
и 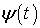 есть медленные (по сравнению с несущей
есть медленные (по сравнению с несущей 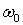 ) регулярные функции, характеризующие законы амплитудной и фазовой модуляции соответственно.
) регулярные функции, характеризующие законы амплитудной и фазовой модуляции соответственно.
В практике радиосвязи и радиолокации возможны случаи приема сигналов, когда неизвестная начальная фаза 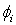 от импульса
от импульса  к импульсу
к импульсу 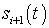 меняется независимо:
меняется независимо:
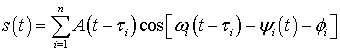 , (10)
, (10)
где 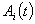 и
и 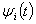 характеризуют медленные (по сравнению с несущей
характеризуют медленные (по сравнению с несущей 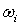 ) процессы, модулирующие амплитуды и фазы элементарных сигналов, соответственно, либо когда случайная фаза всюду одинакова:
) процессы, модулирующие амплитуды и фазы элементарных сигналов, соответственно, либо когда случайная фаза всюду одинакова:
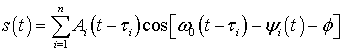 . (11)
. (11)
Распределение начальных фаз в каждом случае равновероятное (9).
1) Пусть требуется обнаружить сложный квазидетерминированный сигнал с флуктуирующей амплитудой и неизвестной начальной фазой
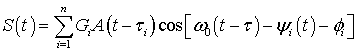 , (12)
, (12)
где распределения 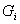 определяются выражением (8). Подставляя (12) в (5), получаем:
определяются выражением (8). Подставляя (12) в (5), получаем:
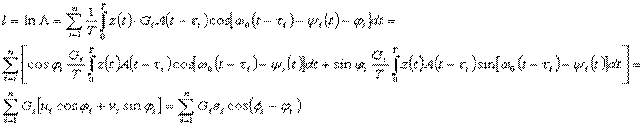
где
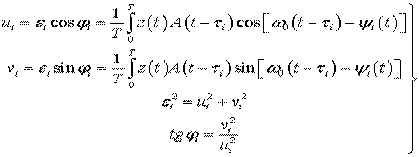 (13)
(13)
Из выражения (13):
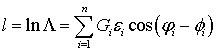 ,
,
получаем, что
 . (14)
. (14)
Усредняя отношение правдоподобия 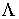 по неизвестным фазам
по неизвестным фазам 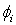 , которые распределены равномерно:
, которые распределены равномерно:
 ,
,
получаем:
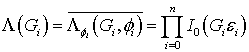 . (15)
. (15)
Полагая все  при
при 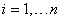 независимыми и распределенными равномерно и усредняя дополнительно по
независимыми и распределенными равномерно и усредняя дополнительно по  , получим:
, получим:
 (16)
(16)
где интеграл в предпоследнем равенстве равен единице в силу условия нормировки плотностей вероятностей (интеграл берется от райсовского распределения). Из (16) получаем алгоритм оптимального приемника обнаружения слабых флуктуирующих сигналов (ФС):
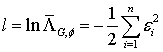 (17)
(17)
Блок-схема приемника, реализующая полученный алгоритм изображена на рис.2.
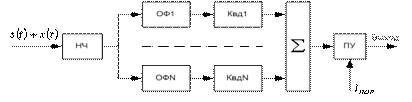
Рис.2 Функциональная схема приемника слабых флуктуирующих сигналов.
Пусть теперь обнаруживается неизвестный радиосигнал, когда в (12) все 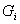 одинаковы. Тогда из (14,15) следует, что:
одинаковы. Тогда из (14,15) следует, что:
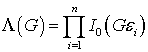 (18)
(18)
откуда после усреднения по 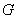 получаем:
получаем:
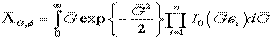 . (19)
. (19)
Интеграл в (19) является неберущимся. Поэтому запишем теперь (18) в виде:
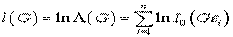 (20)
(20)
и предполагая, в силу малости сигнала 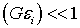 , что
, что 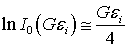 , из (20) получаем:
, из (20) получаем:
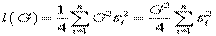 . (21)
. (21)
Усредняя 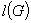 по
по 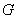 , получим:
, получим:
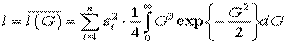 (22)
(22)
Вычислим интеграл в (22) по частям:
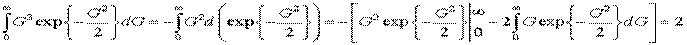 (23)
(23)
ибо интеграл в (23) равен единице в силу условия нормировки. Поэтому алгоритм (22) равен:
 . (24)
. (24)
2) Пусть теперь обнаруживается ФРС, т.е. когда в (12)  различны, а все
различны, а все 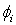 одинаковы, и равны
одинаковы, и равны 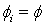 . Тогда из (13) следует что:
. Тогда из (13) следует что:
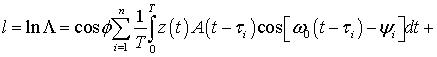
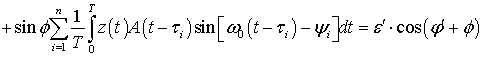 ,
,
и, следовательно
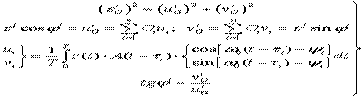 (25)
(25)
Из (25) получаем:
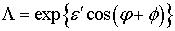 , (26)
, (26)
и после усреднения по случайной фазе 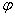 получаем:
получаем:
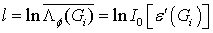 , (27)
, (27)
откуда
 . (28)
. (28)
Усредняя (28) дополнительно по флуктуирующим амплитудам  ,
, 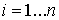 , получаем
, получаем
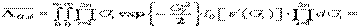
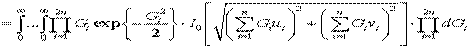 . (29)
. (29)
Поскольку:
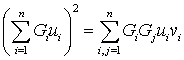 ,
, 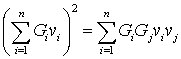
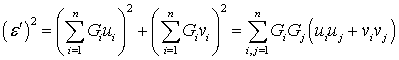 , (30)
, (30)
то выражение (29) равно:
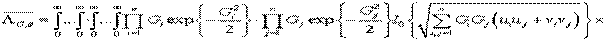
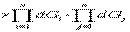 . (31)
. (31)
Интеграл (31) не является табличным. Поэтому, снова обращаясь к (27), в предположении малости огибающей 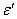 (в силу малости
(в силу малости 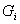 ) получаем:
) получаем:
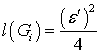 ,
,  (32)
(32)
откуда с учетом выражений (25) и (30) получаем:
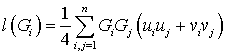 . (33)
. (33)
Усредняя теперь (33) дополнительно по флуктуирующим амплитудам, с использованием выражения (8) получаем:
 , (34)
, (34)
где  , поэтому, вычисляя
, поэтому, вычисляя
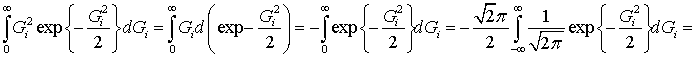
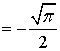 , (35)
, (35)
и подставляя в (34), получаем:
 .
.  (36)
(36)
В соответствии с полученным алгоритмом и с учетом выражений (25) для 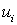 и
и 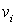 , блок-схема оптимального приемника (рис.3) состоит из НЧ вида (6) и
, блок-схема оптимального приемника (рис.3) состоит из НЧ вида (6) и 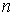 квадратурных каналов. Каждый квадратурный канал состоит из формирователя квадратурных составляющих (Кв), перемножителя (
квадратурных каналов. Каждый квадратурный канал состоит из формирователя квадратурных составляющих (Кв), перемножителя ( 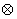 ) и интегратора
) и интегратора 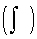 , причем на первые входы перемножителей поступают составляющие
, причем на первые входы перемножителей поступают составляющие 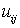 или
или 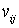 , а на другие входы - опорные квадратурные сигналы от генератора опорных сигналов (ГОС). Составляющие всех каналов
, а на другие входы - опорные квадратурные сигналы от генератора опорных сигналов (ГОС). Составляющие всех каналов 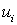 ,
, 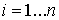 перемножаются при
перемножаются при 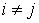 , или возводятся в квадрат при
, или возводятся в квадрат при 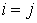 . Аналогично и для составляющих
. Аналогично и для составляющих 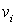 ,
, 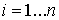 . Произведения вида
. Произведения вида 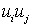 и
и 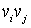 поступают на сумматор
поступают на сумматор 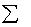 и далее на пороговое устройство.
и далее на пороговое устройство.
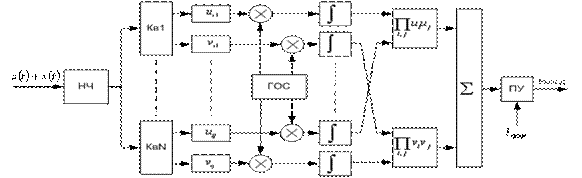
Рис.3 Функциональная схема квадратурного приемника.
, (39)
где функция
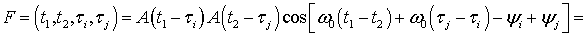
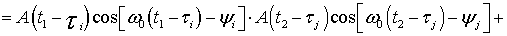
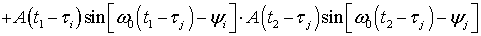 , (40)
, (40)
является опорной и формируется из сигналов ГОС.
3) Пусть требуется обнаружить (ФС), когда в (12) все 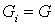 , и
, и  ,
,  . Тогда из (24-26) следует, что
. Тогда из (24-26) следует, что
 (41)
(41)
где
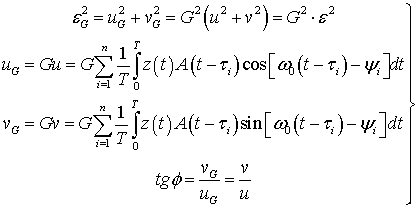 . (42)
. (42)
Усредняя отношение правдоподобия


по фазе 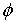 , получаем (15):
, получаем (15):
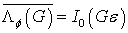 ,
,
и после дополнительного усреднения по 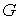 см.(25) получаем:
см.(25) получаем:
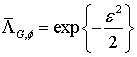 , (43)
, (43)
поэтому в силу монотонности экспоненциальной и квадратичной функций алгоритм оптимального приемника примет вид:
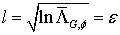 , (44)
, (44)
а блок-схема приемника его реализующая изображена на рис.4, где функциональный узел после сумматора есть детектор огибающей (ДО).
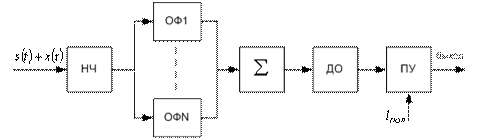
Рис.4 Функциональная схема приемника с “дружно” флуктуирующими параметрами.
Перейдем к вычислению характеристик. Пусть сигнал (12) отсутствует во входной смеси на входе приемника. Тогда в отсутствие сигнала среднее значение случайной величины (17) равно:
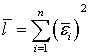 (45)
(45)
ибо 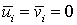 , и
, и  , а дисперсия
, а дисперсия
 . (46)
. (46)
Используя (13), получаем:

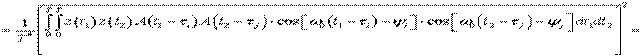
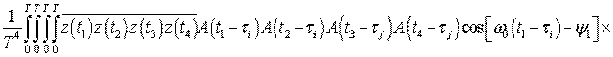
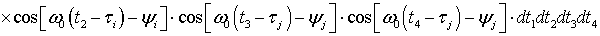 . (47)
. (47)
Рассмотрим отдельно момент 4-го порядка в (47):
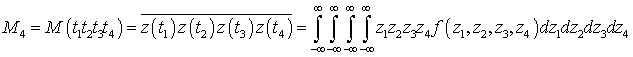 ,
,
(48)
где 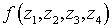 – четырехмерная плотность вероятности. Предполагая, что помеха типа белого шума, получаем [5], что процесс
– четырехмерная плотность вероятности. Предполагая, что помеха типа белого шума, получаем [5], что процесс 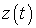 также типа белого шума. Можно показать, что для процессов типа белого шума:
также типа белого шума. Можно показать, что для процессов типа белого шума:
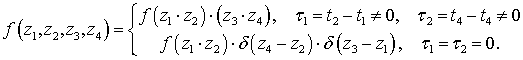
Тогда
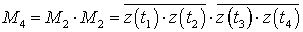 , (49)
, (49)
и из (47) с учетом выводов в [2] получаем:
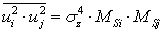 . (50)
. (50)
Аналогично, для 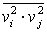 получаем:
получаем:
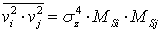 (51)
(51)
Рассмотрим теперь произведение:
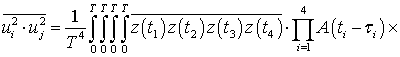
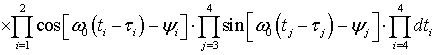
откуда с учетом (49) получаем:
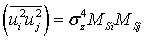 . (52)
. (52)
Подставляя (50) ¸ (52) в (46), получаем:
 . (53)
. (53)
Отметим, что выражение (53) можно получить более простым путем, если учесть [5], что 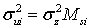 .
.
При наличии сигнала дисперсия величины 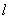 в силу малости сигнала совпадает с (53), а среднее значение равно [3]:
в силу малости сигнала совпадает с (53), а среднее значение равно [3]:
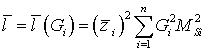 . (54)
. (54)
В отсутствие сигнала распределение величины 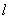 определяется выражением
определяется выражением
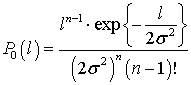 .
.
а вероятность 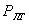 как показано в [3] равна:
как показано в [3] равна:
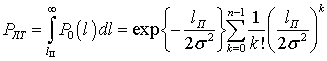

Тогда вероятность правильного обнаружения равна:
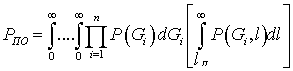 , (55)
, (55)
где, в соответствии с (14):
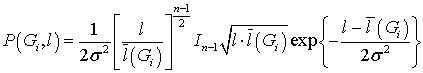 . (56)
. (56)
Интеграл (55) не является табличным, однако с помощью ЭВМ вычислить 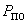 возможно. При
возможно. При 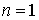 (один элементарный сигнал) соответствующие выражения приведены в [4].
(один элементарный сигнал) соответствующие выражения приведены в [4].
б) Пусть в (12)  одинаковы,
одинаковы, 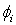 различны, и алгоритм приемника равен (23). Тогда в отсутствие сигнала
различны, и алгоритм приемника равен (23). Тогда в отсутствие сигнала 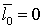 , и
, и 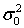 определяется (53). При наличии сигнала дисперсия совпадает с (53), а среднее значение равно:
определяется (53). При наличии сигнала дисперсия совпадает с (53), а среднее значение равно:
 ,
,
Тогда вероятность ложной тревоги равна [4],
 , (57)
, (57)
а вероятность правильного обнаружения равна:
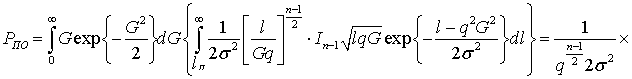

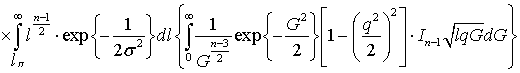 . (58)
. (58)
в) Пусть в (12)  различные, а
различные, а 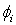 одинаковы, при этом алгоритм соответствует (32). В этом случае
одинаковы, при этом алгоритм соответствует (32). В этом случае 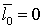 , а выражения для дисперсии и среднего при наличии сигнала получаются довольно громоздкими, поэтому не приводятся. Необходимо отметить, что характеристики качества обнаружения в этом случае будут лучше, чем в случае, когда все
, а выражения для дисперсии и среднего при наличии сигнала получаются довольно громоздкими, поэтому не приводятся. Необходимо отметить, что характеристики качества обнаружения в этом случае будут лучше, чем в случае, когда все 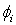 различны (56), но хуже, чем в случае, когда все
различны (56), но хуже, чем в случае, когда все 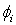 одинаковы, и нет флюктуации амплитуд (30). Этим определены границы вероятностей ложной тревоги и правильного обнаружения.
одинаковы, и нет флюктуации амплитуд (30). Этим определены границы вероятностей ложной тревоги и правильного обнаружения.
г) Пусть в (12) все  и
и 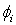 одинаковы, а алгоритм обнаружения соответствует (35). Тогда среднее значение
одинаковы, а алгоритм обнаружения соответствует (35). Тогда среднее значение 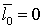 , а дисперсия равна:
, а дисперсия равна:
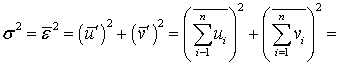
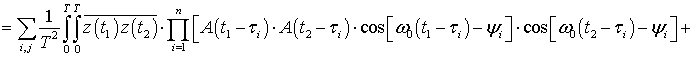
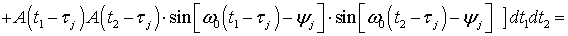
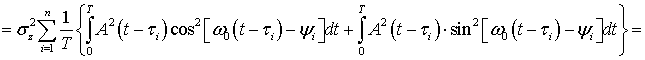
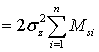 , (59)
, (59)
где при выводе была использована формула [5]:
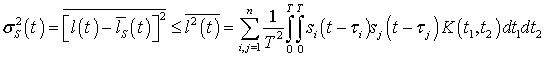 ,
,
где были отброшены интегралы от быстроосциллирующих функций. При наличии сигнала дисперсия определяется формулой (58), а среднее значение с учетом (13) равно:
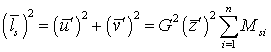 . (60)
. (60)
Вероятность  определяется формулой (57), а
определяется формулой (57), а 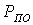 - (58), в которой составляющие
- (58), в которой составляющие  и
и 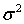 необходимо заменить выражениями (60) и (59) соответственно.
необходимо заменить выражениями (60) и (59) соответственно.
д) Если сигнал (12) обнаруживается на фоне нестационарной помехи, то аналитическое исследование значительно усложняется. Это происходит в силу того, что средние, дисперсии и т.д. будут зависить от времени.
Заключение
Отметим, что в сумматоре происходит как некогерентное, так и когерентное суммировании, ибо хотя начальная фаза 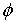 и неизвестна, но она одинакова для всех элементарных сигналов в . По этой причине обработка поступающего сигнала оказывается довольно сложная. Если же элементарные сигналы являются ортогональными, то совершенно очевидно, что
и неизвестна, но она одинакова для всех элементарных сигналов в . По этой причине обработка поступающего сигнала оказывается довольно сложная. Если же элементарные сигналы являются ортогональными, то совершенно очевидно, что 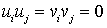 , при
, при 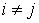 , и из получаем:
, и из получаем:
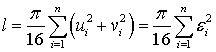 , (37)
, (37)
т.е. алгоритм обработки совпадает (с точностью до мультипликативной константы) с . Полученный результат означает, что независимо от того, одинакова в начальная фаза или нет, структура приемника обнаружения ортогональных сигналов не меняется. С физической точки зрения этот результат понятен, так как рассматриваемые в работе методы синтеза оптимальных приемников являются в принципе амплитудными, то именно вид амплитуды  сигналов определяет структуру обнаружителя в целом. Отметим, что алгоритм допускает некоторое упрощение. Допустим, для общности, что несущие частоты
сигналов определяет структуру обнаружителя в целом. Отметим, что алгоритм допускает некоторое упрощение. Допустим, для общности, что несущие частоты 
 в элементарных сигналах не совпадают. Тогда подставляя
в элементарных сигналах не совпадают. Тогда подставляя 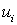 и
и 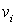 из в легко убедиться, что:
из в легко убедиться, что:
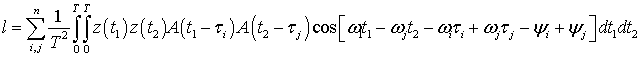 (38)
(38)
Список использованной литературы
1. Зюко А. Г., Кловский Д. Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. – М.: Связь, 1980. – 228 с.: ил.
2. Фалькович С.Е. Оценка параметров сигнала. – М.: Изд-во “Советское радио”, 1970. – 336 с.: ил.
3. Киреев М. А. Выделение полностью известного сигнала на фоне негауссовых помех. Телекоммуникации №3, 2012. – с.13 – 18.
4. Голяницкий И.А. Пространственно-временные статистические характеристики модулированных полей и процессов. – М.: Изд-во МАИ, 1991. – 160 с.: ил.
5. Голяницкий И.А. Оптимальная пространственно-временная обработка негауссовых полей и процессов. – М.: Изд-во МАИ, 1994. – 208 с.: ил.
|
из
5.00
|
Обсуждение в статье: Синтез алгоритмов и схем оптимальных приемников |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

