 |
Главная |
Вычислительный эксперимент
|
из
5.00
|
Запуская программу, появляется главное окно:
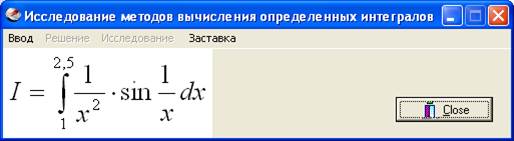
Рис.10. Главное окно.
На нём, как и задумывалось, обозначены: главное меню, состоящее из пунктов «Ввод», «Решение», «Исследование» и «Заставка». После выбора пункта главного меню «Ввод» откроется окно

Рис.11. Окно ввода данных.
В данном окне нужно указать начало и конец промежутка интегрирования, а также количество разбиений. После выполнения этих действий нужно нажать на кнопку «ОК».
Далее в пункте главного меню «Решение» нужно выбрать подпункт «Методом прямоугольников» или подпункт «Методом Симпсона», который определит, при помощи какого метода будет вычисляться определённый интеграл. После щелчка на нужный пункт перед нами появится окно
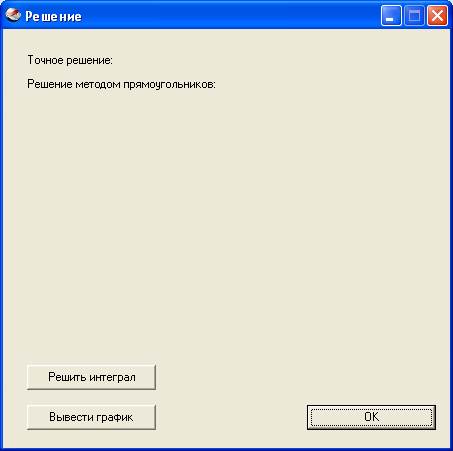
Рис.12. Решение.
Далее нужно нажать на кнопку «Решить интеграл», после чего в верхней части текущего окна появится точное значение, подсчитанное по формуле Ньютона-Лейбница, а также значение, полученное по формуле выбранного метода. При нажатии на кнопку «Вывести график» в середине окна появится график функции с наглядным изображением метода прямоугольников, при условии выбора данного метода решения, или просто график функции при выборе метода Симпсона. Данное окно после выполнения перечисленных действий будет выглядеть следующим образом

Рис.13. Решение методом прямоугольников.
Далее, выбирая пункт меню «Исследование», мы открываем окно, где после щелчка на кнопке «Вывести графики» будут выведены графики зависимости уровня погрешности от количества разбиений для метода прямоугольников (график красного цвета) и метода Симпсона (график зелёного цвета). Под погрешностью подразумевается взятая по модулю разность между точным значением, полученным по формуле Ньютона-Лейбница, и приближённым значением, полученным по формуле прямоугольников или Симпсона, при данном количестве разбиений n, которое меняется в цикле от 10 до 200.

Рис.14. Исследование на погрешность.
Стоит отметить, что в данной программе реализованы функции, предусматривающие обработку исключительных ситуаций, которые могут вызвать сбои в работе программы, при возникновении которых выводится информационное окно с рекомендациями по устранению возникающих неполадок.
Заключение
Проект разработан для вычисления определённого интеграла методами прямоугольников и Симпсона в среде программирования Delphi.
Спроектирован интерфейс программы и написан программный код на языке высокого уровня.
Проведена визуализация метода прямоугольников и анализ данных методов на погрешность вычислений.
В ходе проведения исследования на погрешность было также установлено, что точность вычисления определённого интеграла по формуле Симпсона намного превосходит точность вычисления определённого интеграла по формуле прямоугольников, о чём свидетельствуют графики зависимости уровня погрешности от количества разбиений для метода прямоугольников и метода Симпсона.
|
из
5.00
|
Обсуждение в статье: Вычислительный эксперимент |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

